Perfekt fyrkantig trinomial

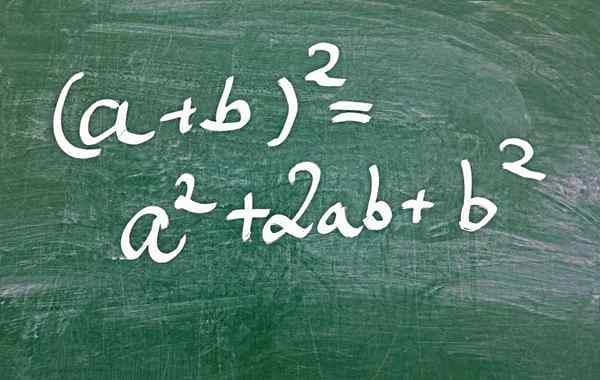Figur 1.- Ett av sätten att få en perfekt fyrkantig trinomial är genom summan

Vad är den perfekta fyrkantiga trinomialen?

Den perfekta fyrkantiga trinomialen är att polynomet på tre termer, varav två är perfekta rutor av mängderna A och B och föregås av samma tecken, medan den tredje termen är exakt den dubbla produkten av A och B, att kunna vara av Ett annat tecken.

En perfekt fyrkantig trinomial erhålls av kvadraten summan eller skillnaden i en binomial och algebraiskt, dess form är som följer:

till² ± 2 ∙ AB + B²

Som framgår innehåller den perfekta fyrkantiga trinomialen:

• Två icke -likartade kvadratiska termer föregick av samma tecken: a² och b²
• En tredje termin 2 ∙ AB, som är den dubbla produkten från kvadratrötterna i de kvadratiska termerna och som kan föregås av ett positivt eller negativt tecken.

Perfekta fyrkantiga trinomialer kan vara en eller flera varierande. Följande trinomial är till exempel en perfekt kvadrat av en variabel:

• x² + 6x + 9

Observera att de första termerna (x²) och tredje (9) är fyrkantiga av de belopp som kallas A och B. Faktiskt, x² Det är kvadratet av x och 9 är kvadratet på 3. På detta sätt kan du skriva följande:

a = x

B = 3

Och den återstående termen är den dubbla produkten av X och 3:

6x = 2 ∙ 3 ​​∙ x

När verifieringen har gjorts är det säkert att denna trinomial är perfekt fyrkantig.

Exempel

figur 2.- Exempel på perfekta fyrkantiga trinomialer. Källa: f. Zapata.

Perfekta fyrkantiga trinomialer visas också i två eller flera variabler, till exempel:

4x² + 4xy + och²

Det är en trinomial i två variabler: "X" och "Y". Det kan säkerställas att det är en perfekt fyrkantig trinomial, eftersom den presenterar två kvadratiska termer:

4x² = (2x)²

och² = (y)²

Och den återstående termen är den dubbla produkten från respektive fyrkantiga rötter: "2x" och "y":

Kan tjäna dig: ortoedro: formler, område, volym, diagonal, exempel

4xy = 2 ∙ 2x ∙ och

Trinomialerna som hittills presenteras är klass 2 i variabeln "X", men de behöver inte nödvändigtvis vara så här. Följande trinomial är klass 4 i "X":

9x⁴ - 30x²Yz + 25y²z²

Det verifieras lätt att detta är en perfekt fyrkantig trinomial. Den första terminen är den perfekta 3x kvadrat², Sedan (3x²)² = 9x⁴.

Termen 25y²z² är lika med (5yz)². Slutligen är den återstående termen 2 ∙ 3x²∙ 5yz = 30 x²och z.

Å andra sidan är trinomialerna som visas nedan inte perfekta fyrkantiga trinomialer:

• x²  + 8x - 16

Det är inte en perfekt fyrkantig trinomial eftersom 16, även om det är 4², Det föregås av ett negativt tecken, medan den andra kvadratiska termen (x²) är positiv.

• x²  - 15x + 25

Det är inte heller en perfekt fyrkantig trinomial, för även om den har två kvadratiska termer: x² och 5², Termen 15x är inte lika med 2 ∙ 5 ∙ x.

• 4x²  + 10x + 32

Denna trinomial är inte perfekt fyrkantig, eftersom den bara innehåller en kvadratisk term: 4x² = (2x)².

Kvadrat av en summa och kvadrat av en skillnad

Perfekta fyrkantiga trinomialer erhålls genom att utveckla två typer av anmärkningsvärda produkter:

• Summan kvadrat.
• Skillnaden.

Först erhålls utvecklingen från den distribuerande egenskapen, eftersom höjning av fyrkantiga binomial betyder att multiplicera den med sig själv:

(A ± B)² = (a ± b) × (a ± b) = a² ± A ∙ B ± B ∙ A + B² = a² ± 2a ∙ B + B²

Trinomialen som erhålls är ett resultat som memoreras med bara lite praxis och är en slags genväg som underlättar utvecklingen, varför den kallas en anmärkningsvärd produkt.

Kan tjäna dig: transcendenta nummer: vad är, formler, exempel, övningar

Följande trinomialer erhålls lätt av anmärkningsvärd produkt, utan att tillämpa distribuerande egendom.

• (x + 6)² = x² + 2 ∙ 6 ∙ x + 6² = x² + 12x + 36
• (2x - 10)² = (2x)² - 2 ∙ 10 ∙ 2x + 10² = 4x² - 40x + 100
• (5y + 2x)² = (5y)² + 2 ∙ 5y ∙ 2x + (2x)² = 25 och² +20xy + 4x²

Faktorisering av en perfekt fyrkantig trinomial

En ofta och nödvändig operation i algebra är faktoriseringen av det perfekta fyrkantiga trinomial, genom vilken trinomialen uttrycks som kvadratet för en summa eller en subtraktion av två termer (en binomial).

Det är den omvända operationen att utveckla den anmärkningsvärda produkten, eftersom tanken har den resulterande trinomialen är att få binomialen som ger upphov till den när den stiger till 2.

Till exempel i den tidigare analyserade 4x perfekta fyrkantiga trinomialen² + 4xy + och², Vad är binomialen att när det är kvadrat ger det upphov till dig?

De respektive fyrkantiga rötter i de kvadratiska termerna är:

√ (4x²) = 2x

Vilket motsvarar: 4x² = (2x)²

√ (och²) = y

Motsvarande att säga att: och² = (y)²

Därför:

4x² + 4xy + och² = (2x + y)²

Och vad är binomialen som har sitt ursprungliga fyrkantiga trinomial 9x⁴ - 30x²Yz + 25y²z²? Återigen extraheras de kvadratiska rötterna i de kvadratiska termerna:

√ (9x⁴) = 3x²

√ (25 och²z²) = 5yz

Så:

(3x² - 5yz)² = 9x⁴ - 30x²Yz + 25y²z²

Löst övningar

Övning 1

I vart och ett av följande trinomialer, slutför det tomma med termen som saknas för att vara en perfekt fyrkantig trinomial:

a) m² + 18m + _____

b) 4x² - _____ + 64

c) _____ + 30n + 25

• Lösning till

Enligt formeln för den anmärkningsvärda produkten:

Kan tjäna dig: kompletterande vinklar: vilka och hur de beräknas, exempel, övningar

(A ± B)² = A² ± 2a ∙ B + B²

Av trinomialen:

m² + 18m + _____

Det följer att:

a = m (så att det² = m²)

Dessutom är den centrala termen: 2 ∙ A ∙ B = 2M ∙ B = 18M, därför B = 9 och dess kvadrat är 9² = 81. Kille efter formeln för den anmärkningsvärda produkten, trinomialen är så här:

(M + 9)² = M² + 18m + 81

• Lösning B

I denna trinomial:

4x² - _____ + 64

Du kan veta och b:

A = √ (4x²) = 2x

B = √64 = 8

Därför är den saknade termen den dubbla produkten av A och B:

2 ∙ AB = 2 ∙ 8 ∙ 2x = 32x

Och det sökande trinomet är:

4x² - 32x + 64

• Lösning C

I trinomialen:

_____ + 30n + 25

Den första terminen saknas, men det är känt att:

B = √25 = 5

OCH

2 ∙ AB = 2 ∙ A ∙ 5 = 10A = 30N

Därför är a = 3n och de sökande trinomialerna:

9n² + 30n + 25

Övning 2

Kontrollera att nästa är en perfekt fyrkantig trinomial och faktor den:

16y² - 24yz + 9z²

• Lösning

Först är det bevisat att de kvadratiska termerna föregås av samma tecken och sedan hittas respektive fyrkantiga rötter:

A = √ (16y²) = 4y

B = √ (9Z²) = 3Z

Då måste du verifiera om den återstående termen är den dubbla produkten av A och B:

2 ∙ AB = 2 ∙ 4y ∙ 3Z = 24yz

Om det är, kan trinomial vara faktor som kvadratet för en skillnad, eftersom den centrala termen föregås av ett negativt tecken:

16y² - 24yz + 9z² = (4y - 3z)²

Referenser

1. Jiménez, r. 2008. Algebra. Prentice hall.
2. Kate's Math Lessons. Perfekta fyrkantiga trinomialer. Återhämtat från: KatesMathlessons.com.
3. Stewart, J. 2006. Preccculment: Matematik för beräkning. Femte. Utgåva. Cengage Learning.
4. Zill, D. 2008. Preccculment med beräkningsförskott. 4th. Utgåva. McGraw Hill.