Aktuella värdegenskaper, formler och exempel

han nuvarande värde (VA) är nuvärdet för en framtida summa pengar eller kassaflöden, med hänsyn till en specifik lönsamhetsgrad, börjar vid värderingstillfället. I redovisning är det indikatorkonceptet så att tillgångar och skulder mäts till det nuvarande värde som de kan säljas eller likvideras till det aktuella datumet.

Framtida belopp måste hantera inflations- eller deflationstryck, med möjlighetskostnader och andra risker som påverkar värdet på det slutliga beloppet. Det verkliga motsvarande värde på ett belopp i framtiden kommer inte att vara samma belopp som en summa pengar idag. Det är där det nuvarande värdet spelar in.

Källa: Pixabay.com

Om du har en uppskattning av vad som kan erhållas med en investering idag kan det enkelt uppskattas hur mycket detta framtida värde skulle vara värt. Alternativt indikerar det nuvarande värdet också det belopp som skulle behövas för att investera idag om du vill avsluta med ett slutligt globalt belopp, förutsatt en viss prestanda.

[TOC]

Egenskaper

En investerare som har pengar har två alternativ: spendera det nu eller spara det. Ekonomisk kompensation för att spara den och inte spendera den är att det monetära värdet kommer att ackumuleras genom det sammansatta räntan som du kommer att få från en låntagare eller bank.

För att utvärdera det verkliga värdet på en summa pengar idag efter en viss tid, kombinerar ekonomiska agenter beloppet till en viss ränta.

Driften av att utvärdera ett nuvarande värde i det framtida värdet kallas kapitalisering. Till exempel, hur mycket kommer det nuvarande $ värdet på fem år?

Den omvända operationen, som utvärderar det nuvarande värdet på en framtida belopp, kallas rabatten. Till exempel, hur mycket kommer de 100 $ som mottas på 5 år, i ett lotteri idag?

Kan tjäna dig: ersätta produkter: egenskaper och exempel

Nuvarande värde i redovisning

Det nuvarande värdet är användbart när det har varit en längre period av överdriven inflation. Under dessa förhållanden kommer de historiska värdena där tillgångarna och skulderna registrerades att vara mycket lägre än deras nuvarande värden.

Det finns emellertid ingen hög grad av acceptans av begreppet nuvarande värde i redovisning. Presenterar följande problem:

Bokföringskostnad

Tid behövs för att samla in aktuell värdeinformation. Därför ökar detta kostnaden och tiden i samband med genereringen av finansiella rapporter.

Informationstillgänglighet

Det kan vara svårt eller omöjligt att få information om aktuell värde om vissa tillgångar och skulder.

Informationsnoggrannhet

Viss information om det nuvarande värdet kan baseras mindre på fakta och mer på antaganden eller dåligt grundade uppskattningar, vilket påverkar tillförlitligheten i de finansiella rapporterna när denna information ingår.

Formler

Det nuvarande värdet är en formel som används i finans som beräknar nuvärdet för ett belopp som kommer att tas emot på ett framtida datum. Förutsättningen för ekvationen är att det finns ett "värde på pengar över tid".

Värdet på pengar över tid är konceptet som indikerar att mottagandet idag är mer än att få samma artikel på ett framtida datum.

Antagandet är att det är att föredra att få $ 100 idag än att få samma summa pengar inom ett år från och med idag. Men vad händer om alternativen var mellan att få $ 100 i nuet eller $ 106 på ett år från och med idag?

En formel behövs som kan ge en kvantifierbar jämförelse mellan ett nuvarande belopp och ett belopp vid en framtida tidpunkt, när det gäller dess nuvarande värde.

Kan tjäna dig: utvinningsaktiviteter: egenskaper, typer och exempel

Va = fn / (1+r) ^n, där

Fn = framtida värde i period n.

R = returnivå eller lönsamhet.

n = antal perioder.

Användning av formeln

Formeln för det nuvarande värdet har ett brett utbud av användningsområden. Därför kan det tillämpas på olika finansområden, inklusive företags ekonomi, bank och investeringar. Det används också som en del av andra finansiella formler.

Hur beräknas det aktuella värdet?

Anta att du för närvarande har $ 1000 och 10% årlig ränta. Detta innebär att pengar växer 10% varje år, på ett sådant sätt:

$ 1000 x (10%= 100) = $ 1100 x (10%= 110) = $ 1210 x (10%= 121) = $ 1331, etc.

-Nästa år kommer $ 1100 att vara samma som $ 1000 nu.

-På två år kommer $ 1210 att vara samma som $ 1000 nu.

-På tre år kommer $ 1331 att vara samma som $ 1000 nu.

Faktum är att alla dessa belopp kommer att vara desamma i tid, med tanke på när de inträffar och med 10% årlig ränta.

Istället för att lägga till 10% varje år är det lättare att multiplicera med 1.10. På detta sätt erhålls följande: $ 1000 x 1,10 = $ 1100 x 1,10 = $ 1210 x 1,10 = $ 1331, etc.

Beräkna det framtida värdet hittills

För att veta vilka pengar i framtiden är för närvarande värt det, beräknas de bakåt, delas med 1.10 varje år, istället för att multiplicera.

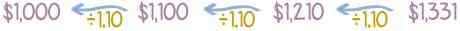
Anta till exempel att det lovas att betala $ 500 nästa år. Räntan är 10%. För att veta vad som är värdet på det beloppet idag är det framtida värdet på $ 500 uppdelat med 1,10, vilket är lika med $ 454,55 som nuvarande värde.

Anta nu att det lovas att betala $ 900 på tre år. För att veta värdet på det beloppet idag delas det framtida beloppet med 1,10 tre gånger. Således skulle $ 900 på 3 år för närvarande vara: $ 900 ÷ 1,10 ÷ 1,10 ÷ 1,10 = $ 900 ÷ (1,10 × 1,10 × 1,10) = $ 900 ÷ 1 331 = $ 676,18 Nu nu.

Kan tjäna dig: inventeringsrotation

Exempel

Exempel 1

En individ vill bestämma hur mycket pengar som skulle behöva placera på sitt penningmarknadskonto för att få 100 $ på ett år från och med idag, om den tjänar 5% ränta på deras konto.

De 100 $ som jag skulle vilja få ett år anger F1 -delen av formeln, 5% skulle vara R, och antalet perioder skulle helt enkelt vara 1. Att sätta detta i formeln skulle det finnas VA = $ 100 / 1.05 = $ 95.24. Idag bör jag sätta in $ 95,24 för att få $ 100 inom ett år, till en ränta på 5% ränta.

Exempel 2

Anta att ett belopp idag deponeras på ett konto, som tjänar 5% ränta årligen. Om målet är att ha $ 5.000 på kontot i slutet av sex år vill du veta hur mycket du ska sätta in på kontot idag. För detta används den aktuella värdeformeln:

Nuvarande värde = framtida värde / (1 + räntesats) ^ antal perioder.

Infoga den kända informationen har du:

VA = $ 5.000 / (1 + 0,05) ^ 6 = $ 5.000 / (1 3401) = $ 3.731.

Referenser

1. Steven Bragg (2018). Aktuell värdebokföring. Bokföringsverktyg. Taget från: AccountOools.com.
2. Finansformler (2019). Nuvarande värde. Taget från: FinanceFormulas.netto.
3. Mathsisfun (2019). Nuvärdet (PV). Taget från: Mathsisfun.com.
4. DQYDJ (2019). Nuvärde kalkylator och förklaring av nuvärdeformeln. Taget från: dqydj.com.
5. Pamela Peterson (2019). Nuvärde exempel. James Madison University. Taget från: utbildning.Jmu.Edu.
6. Wikipedia, The Free Encyclopedia (2019). Nuvarande värde. Taget från: i.Wikipedia.org.