Vektoregenskaper och egenskaper, element, typer, exempel

De vektorer Det är matematiska enheter som har en storlek -positiv -vanligtvis åtföljd av en måttenhet, utöver riktning och mening. Sådana egenskaper är mycket lämpliga för att beskriva fysiska mängder som hastighet, styrka, acceleration och många fler.

Med vektorer är det möjligt att utföra operationer som summa, subtraktion och produkter. Divisionen är inte definierad för vektorer och när det gäller produkten finns det tre klasser som vi kommer att beskriva senare: skal- eller punktprodukt, vektor eller tvärprodukt och produkt av en skalar för en vektor.

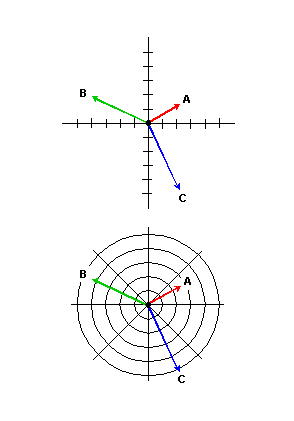
Figur 1. Elementen i en vektor. Källa: Wikimedia Commons.

För att helt beskriva en vektor är det nödvändigt att indikera alla dess egenskaper. Storleken eller modulen är ett numeriskt värde åtföljt av en enhet, medan riktning och mening är etablerade med hjälp av ett koordinatsystem.

Låt oss titta på ett exempel: Anta att ett plan flyger från en stad till en annan med en hastighet av 850 km/h i riktningen. Här har vi en helt specificerad vektor, eftersom storleken är tillgänglig: 850 km/h, medan riktning och mening är NE.

Vektorer representeras vanligtvis grafiskt av orienterade linjesegment, vars längd är proportionell mot storleken.

För att specificera riktningen och betydelsen krävs en referenslinje som vanligtvis är den horisontella axeln, även om norr också kan tas som referens, så är fallet med planets hastighet:

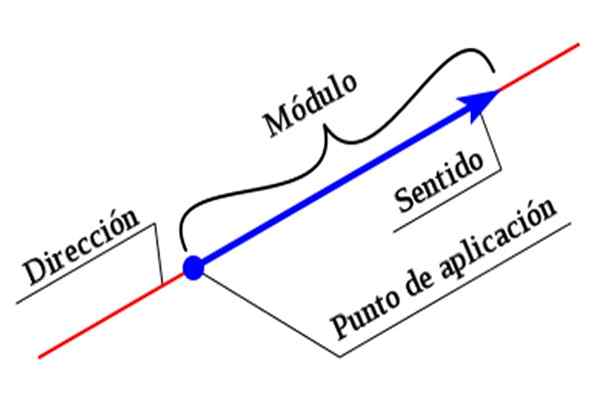
figur 2. En hastighetsvektor. Källa: f. Zapata.

Figuren visar hastighetsvektorn på planet, som betecknas som v i djärv, För att skilja det från en skalform, som bara kräver ett numeriskt värde och någon enhet som ska anges.

[TOC]

Element i en vektor

Som vi har sagt är vektorelementen:

-Storlek eller modul, ibland även kallad absolut värde eller vektorstandard.

-Adress

-Känsla

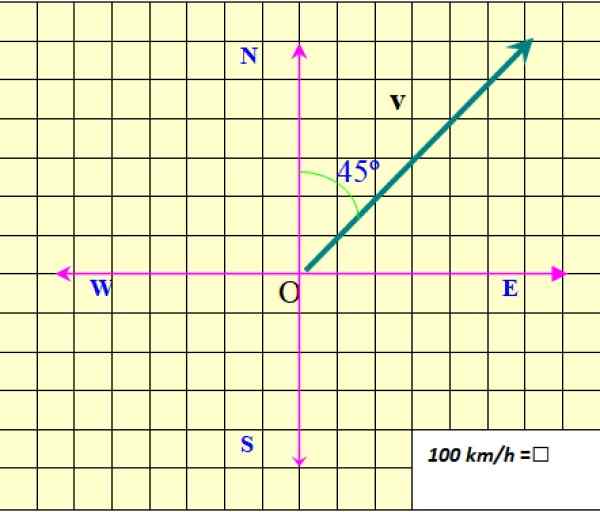
I exemplet i figur 2, modulen för v Det är 850 km/h. Modulen betecknas som V utan djärv, eller som |v|, Där staplarna representerar det absoluta värdet.

Adressen till v anges med avseende på norr. I detta fall är det 45º norr om öst (45º NE). Slutligen informerar pilens spets om riktningen för v.

I det här exemplet har vektorns ursprung ritats genom att sammanfalla med ursprunget eller koordinatsystemet, detta kallas Länkad vektor. Å andra sidan, om vektorns ursprung inte matchar referenssystemets, sägs det att det är en fri vektor.

Det bör noteras att för att helt ange vektorn måste dessa tre element anges, annars skulle beskrivningen av vektorn vara ofullständig.

Rektangulära komponenter i en vektor

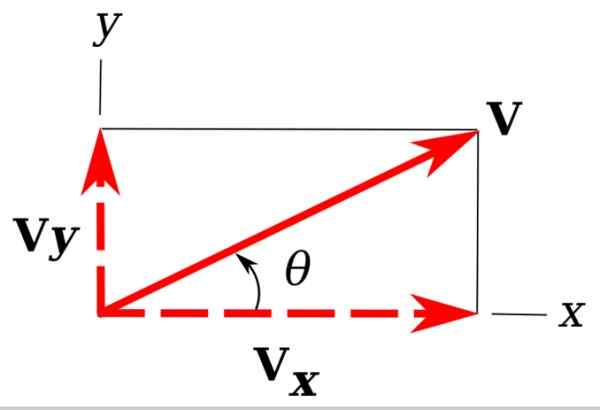Figur 3. Rektangulära komponenter i en vektor i planet. Källa: Wikimedia Commons. Unther [CC BY-SA 3.0 (https: // CreativeCommons.Org/licenser/BY-SA/3.0)]

På bilden har vi tillbaka vår exempelvektor v, det är i planet Xy.

Det är lätt att märka att V -prognoser på X- och Y -koordinataxlarna bestämmer en höger triangel. Dessa prognoser är v_och och v_x och kallas rektangulära komponenter i v.

Ett sätt att beteckna v Genom sina rektangulära komponenter är det så här: v = x, v_och>. Dessa fyrkantiga parenteser används istället för parentes för att betona det faktum att det är en vektor och inte en punkt, eftersom i detta fall skulle parentes användas.

Kan tjäna dig: James Chadwick: Biografi, atommodell, experiment

Om vektorn är i det tre dimensionella utrymmet behövs en komponent till, så att:

v = x, v_och, v_z>

Genom att känna till de rektangulära komponenterna beräknas vektorns storlek, vilket motsvarar att hitta hypotenusen för den högra triangeln vars ben är v_x och v_och,. Genom Pythagoras teorem följer det att:

|v|² = (v_x)² +  (v_och)²

Polär form av en vektor

När vektorstorleken är känd |v| Och vinkeln θ som denna form med referensaxeln, vanligtvis den horisontella axeln, är vektorn lika specificerad. Det sägs då att vektorn uttrycks i polär form.

Rektangulära komponenter i detta fall beräknas enkelt:

v_x = |v|.cos θ

v_och = |v|.synd θ

Enligt ovanstående är de rektangulära komponenterna i hastighetsvektorn v av planet skulle vara:

v_x = 850 . cos 45º km/h = 601.04 km/h

v_och = 850 . Sen 45º km/h = 601.04 km/h

Grabbar

Det finns olika typer av vektorer. Det finns venvektorer, position, förskjutning, kraft, elektriskt fält, mängden rörelse och många fler. Som vi redan har sagt, i fysiken finns det många vektorstorlekar.

När det gäller vektorer som har vissa egenskaper kan vi nämna följande typer av vektorer:

-Null: Dessa är vektorer vars storlek är 0 och som betecknas som 0. Kom ihåg att den djärva bokstaven symboliserar de tre grundläggande egenskaperna hos en vektor, medan den normala bokstaven endast representerar för modulen.

Till exempel om en kropp i statisk balans måste summan av krafter vara en nollvektor.

-Gratis och kopplad: Fria vektorer är de vars ursprungspunkter och ankomst är alla par av planen eller rymden, till skillnad från länkade vektorer, vars ursprung sammanfaller med det för referenssystemet som används för att beskriva dem.

Paret eller ögonblicket som produceras av ett par krafter är ett bra exempel på fri vektor, eftersom vridmomentet inte gäller någon särskild punkt.

-Utrustning: De är två fria vektorer som delar identiska egenskaper. Därför har de samma storlek, riktning och mening.

-Coplanares eller Coplanarios: vektorer som tillhör samma plan.

-Motsats: vektorer med lika stor storlek och riktning, men motsatta sinnen. Vektorn i motsats till en vektor v Det är vektorn -v Och summan av båda är nollvektorn: v + (-v) = 0.

-Samverkande: vektorer vars handlingslinjer alla passerar genom samma punkt.

-Glida: är de vektorer vars applikationspunkt kan glida längs en viss linje.

-Colineal: vektorer som finns på samma linje.

-Enheter: De vektorer vars modul är 1.

Ortogonal enhetsvektorer

Det finns en mycket användbar typ av vektor i fysik som kallas ortogonal enhetsvektor. Den ortogonala enhetsvektorn har en modul som är lika med 1 och enheterna kan vara alla, till exempel de med hastighet, position, styrka eller annat.

Det finns en uppsättning speciella vektorer som hjälper enkelt att representera andra vektorer och utföra operationer med dem: de är ortogonala enhetsvektorer Yo, J och k, Enheter och vinkelrätt mot varandra.

I två dimensioner riktas dessa vektorer genom den positiva känslan av båda axlarna x från axeln och. Och i tre dimensioner tillsätts en enhetsvektor i axelns riktning z positiv. De representeras enligt följande:

Kan tjäna dig: vad är strukturen för dokumentär forskning?

Yo =

J =

k =

En vektor kan representeras av enhetsvektorer Yo, J och k som följer:

v = v_x Yo + v_och J + v_z k

Till exempel hastighetsvektorn v Från de tidigare exemplen kan du skriva som:

v = 601.04 Yo + 601.04 J km/h

Komponenten i k Det är inte nödvändigt, eftersom denna vektor är i planet.

Summan av vektorer

Summan av vektorer förekommer mycket ofta i olika situationer, till exempel när du vill hitta den resulterande kraften på ett objekt som påverkas av olika krafter. För att börja anta att du har två fria vektorer eller och v På planet, som följande visar vänster:

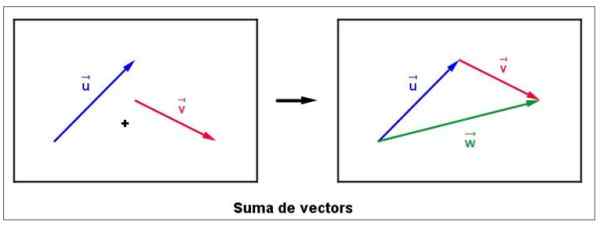Figur 4. Grafisk summa av två vektorer. Källa: Wikimedia Commons. LLUC CABANACH [CC BY-SA 3.0 (https: // CreativeCommons.Org/licenser/BY-SA/3.0)].

Han flyttar omedelbart till vektorn v, utan att modifiera dess storlek, riktning eller mening, så att det härstammar sammanfaller med slutet av eller.

Sumvektorn kallas W och ritas med början från att du slutar i v, Enligt rätt figur. Det är viktigt att notera att vektorns storlek W Det är inte nödvändigtvis summan av storleken på v och eller.

Om det återspeglas noggrant i detta avseende, det enda tillfället när storleken på den resulterande vektorn är summan av tilläggens storlekar, är det när båda missbrukarna är i samma riktning och har samma betydelse.

Och vad händer om vektorerna inte är fria? Det är också väldigt enkelt att lägga till dem. Vägen att göra är att lägga till komponentkomponent eller analytisk metod.

Som ett exempel, låt oss överväga vektorerna i följande figur, det första är att uttrycka dem från en av de kartesiska formerna som tidigare förklarats:

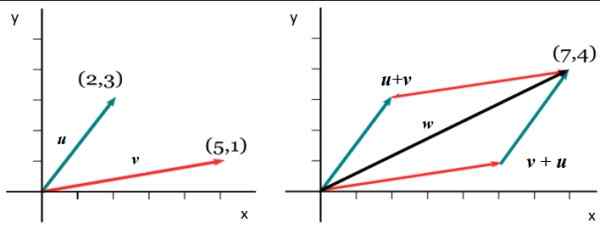Figur 5. Summan av två länkade vektorer. Källa: Wikimedia Commons.

v =

eller =

För att få komponenten i x av vektorn tillägg W, De respektive komponenterna läggs till i x av v och eller: W_x = 5+2 = 7. Och att få W_och En analog procedur följs: W_och = 1+3. Därför:

eller =

Egenskaper för summan av vektorer

-Summan av två eller flera vektorer resulterar i en annan vektor.

-Det är kommutativt, tilläggsordningen ändrar inte summan, så att:

eller + v = v + eller

-Det neutrala elementet i summan av vektorer är nollvektorn: v + 0 = v

-Subtraktionen av två vektorer definieras som summan av det motsatta: v - u = v + (-eller)

Exempel på vektorer

Som vi har sagt finns det många vektormängder i fysiken. Bland de mest kända är:

-Placera

-Förflyttning

-Medelhastighet och omedelbar hastighet

-Acceleration

-Tvinga

-Rörelse

-Vridmoment eller kraft av kraft

-Impuls

-elektriskt fält

-Magnetiskt fält

-Magnetiskt ögonblick

Å andra sidan är de inte vektorer utan klättrar:

-Tid

-Massa

-Temperatur

-Volym

-Densitet

-Mekaniskt arbete

-Energi

-Värme

-Kraft

-Spänning

-Elektrisk ström

Andra operationer mellan vektorer

Förutom summan och subtraktionen av vektorer finns det tre andra operationer mellan mycket viktiga vektorer, eftersom de ger upphov till nya mycket viktiga fysiska storlekar:

-Produkt av en skalar för en vektor.

-Den skalära produkten eller punktprodukten mellan vektorer

-Och tvär- eller vektorprodukten mellan två vektorer.

Produkt av en skalar för en vektor

Tänk på Newtons andra lag, som säger att kraften tvingar F och acceleration till De är proportionella. Proportionalitetskonstanten är massan m av objektet därför:

F = m.till

Degen är en skalar; För sin del är styrka och acceleration vektorer. Eftersom kraften erhålls genom att multiplicera massan med accelerationen är det resultatet av produkten från en skalar av en vektor.

Kan tjäna dig: exempel på teoretiska ramverk

Denna typ av produkt resulterar alltid i en vektor. Här ett annat exempel: mängden rörelse. Vara P Vektormängden rörelse, v Hastighetsvektorn och som alltid, m är massan:

P = m.v

Skalprodukt eller punktprodukt mellan vektorer

Vi har placerat mekaniskt arbete i listan över storlekar som inte är vektorer. Arbetet i fysik är emellertid resultatet av en operation mellan vektorer som kallas en skalprodukt, intern produkt eller punktprodukt.

Vara vektorerna v och eller, Poängen eller klättringsprodukten definieras mellan dem:

v∙eller = |v| ∙ |eller |.cos θ

Att vara θ vinkeln mellan dem. Från den visade ekvationen dras det omedelbart att resultatet av punktprodukten är en skalar och att om båda vektorerna är vinkelräta är deras skalära produkt 0.

Tillbaka till mekaniskt arbete W, Detta är den skalära produkten mellan styrka vektor F och vektorförskjutningen ℓ.

W = F∙ℓ                  

När vektorer är tillgängliga i termer av sina komponenter är punktprodukten också mycket enkel att beräkna. Ja v = x, v_och, v_z > och eller = x, eller_och, eller_z >, Poängprodukten mellan de två är:

v∙eller = v_x eller_x + v_och eller_och + v_z eller_z

Poängprodukten mellan vektorer är därför kommutativ:

v∙eller = eller∙v

Korsprodukt eller vektorprodukt mellan vektorer

Ja v och du är våra två exempelvektorer, vektorprodukten definieras som:

v x eller = W

Det följer omedelbart att tvärprodukten resulterar i en vektor, vars modul definieras som:

|v x u | = | V | . | u |. synd θ

Var θ Det är vinkeln mellan vektorerna.

Korsprodukten är därför inte kommutativ v x u ≠ u x v. Faktiskt v x U = - (u x V).

Om de två exempelvektorerna uttrycks i termer av enhetsvektorerna underlättas beräkningen av vektorprodukten:

v = v_x Yo + v_och J + v_z k

eller = u_x Yo + eller_och J + eller_z k

Korsprodukter mellan enhetsvektorer

Korsprodukten mellan identiska enhetsvektorer är noll, eftersom vinkeln mellan dem är 0º. Men bland olika enhetsvektorer är vinkeln mellan dem 90º och SIN 90º = 1.

Följande schema hjälper till att hitta dessa produkter. I pilens riktning är det positivt och i motsatt riktning:

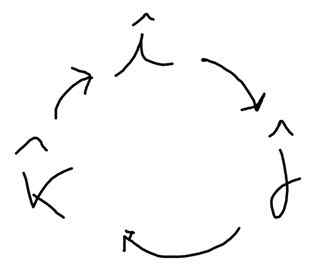
Yo x J = k, j x k = Yo; k x Yo = J; J x i = -k; k x J = -Yo; Yo x k = -J

Tillämpa distribuerande egendom, som förblir giltig för produkter bland vektorer plus egenskaperna hos enhetsvektorer, du har:

v x eller = (v_x Yo + v_och J + v_z k) X (u_x Yo + eller_och J + eller_z k) =  

= (v_ocheller_z - v_zeller_och )Yo + (v_zeller_x - v_xeller_z )J + (v_xeller_och - v_ocheller_x )k

Löst övningar

- Övning 1

Med tanke på vektorerna:

v = -5 Yo + 4J + 1 k

eller = 2 Yo -3 J + 7k

Vad ska vara vektorn W så att summan v + eller + W resultat 6 Yo +8 J -10k?

Lösning

-5 Yo + 4J + 1 k

2 Yo -3 J + 7k

 W_x Yo + W_och J + W_z k  +

--

6Yo + 8 J -10 k

Därför måste det uppfyllas att:

-5 +2 + w_x = 6 → W_x = 9

4-3 + w_och = 8 → W_och = 7

1 + 7 + w_z = -10 → W_z = -18

Svaret är: W = 9 Yo +7 J - 18k

- Övning 2

Vad är vinkeln mellan vektorerna v och eller av övning 1?

Lösning

Vi kommer att använda skalprodukten. Vi har:

cos θ = v∙eller / |v| ∙ |eller|

v∙eller= -10 -12+7 = -15

|v| = √ (-5)² +4² +1²= √42 = 6.48

|eller| = √2² +(-3)² +7²= √62 = 7.87

Ersätta dessa värden:

cos θ = -15 / 6.48 x 7.87 = -0.2941 → θ = 107.Första

Referenser

1. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volym 1. Kinematik. Redigerad av Douglas Figueroa (USB).
2. Giancoli, D.  2006. Fysik: Principer med applikationer. Sjätte. Ed Prentice Hall.
3. Rex, a. 2011. Fysikens grunder. Pearson.
4. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14th. Ed. Volym 1.
5. Serway, R., Jewett, J. 2008. Fysik för vetenskap och teknik. Volym 1. 7th. Ed. Cengage Learning.