Genomsnittliga hastighetsformler, hur det beräknas och löses träning

De medelhastighet För en mobilpartikel definieras den som orsaken mellan variationen i den position hon upplever och tidsintervallet som används i förändringen. Den enklaste situationen är en där partikeln rör sig längs en rak linje representerad av X -axeln.

Anta att det mobila objektet upptar X -positionerna₁ och x₂ I tider t₁ och t₂ respektive. Definitionen av medelhastighet v_m Det representeras matematiskt på följande sätt:

Enheterna av v_m I internationellt system är de meter/andra (m/s). Andra vanliga användningsenheter som visas i mobila texter och enheter är: km/h, cm/s, miles/h, fötter/s och mer, förutsatt att de är längden/tidsformuläret.

Den grekiska bokstaven "Δ" läser "delta" och används för att sammanfatta skillnaden mellan två mängder.

[TOC]

Egenskaper för medelhastighetsvektorn V_m

Medelhastigheten är en viktig egenskap hos rörelse. Källa: Pixabay

Medelhastigheten är en vektor, eftersom den är relaterad till förändringen av position, som i sin tur är känd som Vektorförskjutning.

Denna kvalitet representeras i fetstil eller av en pil över bokstaven som anger storleken. I en dimension är emellertid den enda möjliga riktningen för x -axeln och kan därför fördelas med vektorotationen.

Eftersom vektorerna har storlek, riktning och mening, indikerar en initial blick på ekvationen att medelhastigheten kommer att ha samma riktning och känsla som förskjutningen.

Föreställ dig partikeln i exemplet som rör sig längs en rak linje. För att beskriva din rörelse är det nödvändigt att indikera en referenspunkt, som kommer att vara "ursprunget" och kommer att betecknas som eller.

Partikeln kan röra sig eller närma sig eller, antingen till vänster eller till höger. Du kan också använda mycket eller lite tid för att nå en viss position.

Det kan tjäna dig: värme: formler och enheter, egenskaper, hur det mäts, exempel

Storleken som har nämnts: position, förskjutning, tidsintervall och medelhastighet, beskriver partikelns beteende under rörelse. Det handlar om storleken Kinematisk.

För att skilja positionerna eller platserna till vänster om eller skylten (-) används och de som finns till höger om eller bär skylten (+).

Medelhastigheten har en geometrisk tolkning som kan ses i följande figur. Det är lutningen på linjen som passerar genom P- och Q -punkterna. När du skär till positionen vs position. tid på två punkter är det en linje torkning.

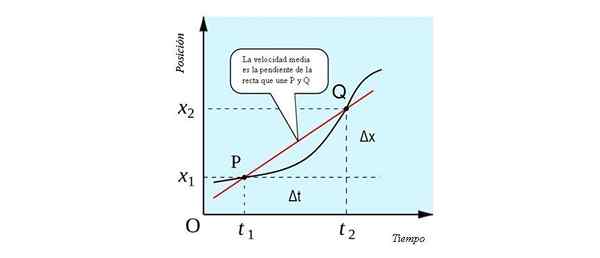Geometrisk tolkning av medelhastigheten, som en lutning av linjen som ansluter sig till P- och Q -punkterna. Källa: すじにく シチュー [CC0].

Tecken på medelhastighet

För följande analys måste det beaktas att t₂ > t₁. Det vill säga följande ögonblick är alltid större än den nuvarande. Den här vägen t₂ - t₁ Det är alltid positivt, vilket vanligtvis är vettigt dagligen.

Då bestäms tecknet på medelhastigheten av x₂ - x₁. Lägg märke till att det är viktigt.

Eller "framåt" eller "tillbaka", som läsaren föredrar.

Om medelhastigheten är positiv betyder det det i genomsnitt värdet av "x”Ökar över tiden, även om detta inte betyder att det kunde ha minskat någon gång i den tid som övervägs - ΔT -.

Men i globala termer, i slutet av tiden ΔT, Hon slutade med en större position än den hon hade i början. Detaljerna om rörelsen ignoreras i denna analys.

Du kan tjäna dig: Newtons tredje lag: applikationer, experiment och övningar

Vad händer om medelhastigheten är negativ? Det betyder att partikeln slutar med en mindre koordinat än den som den började. Groso -läge rörde sig bakåt. Låt oss titta på några numeriska exempel:

Exempel 1: Med tanke på de initiala och slutliga positionerna som anges, ange tecknet på medelhastigheten. Var rörde sig partikeln globalt?

yxa₁ = 3 m; x₂ = 8 m

Svar: x₂- x₁  = 8 m - 3 m = 5 m. Positiv medelhastighet, partikeln gick framåt.

b) x₁ = 2 m; x₂ = -3 m

Svar: x₂ - x₁ = -3 m -2 m = -5 m. Genomsnittlig negativ hastighet, partikeln rörde sig bakåt.

 c) x₁  = - 5 m; x₂ = -12 m

Svar: x₂ - x₁   = -12 m -( -5 m) = -7 m. Genomsnittlig negativ hastighet, partikeln rörde sig bakåt.

d) x₁  = - 4 m; x₂ = 10 m

Svar: x₂ - x₁  = 10 m - (-4 m) = 14 m. Positiv medelhastighet, partikeln gick framåt.

Kan medelhastigheten vara 0? Ja. Så länge utgångspunkten och ankomstpunkten är desamma. Betyder det att partikeln nödvändigtvis var i vila hela tiden?

Nej, det betyder bara att resan var tur och retur. Kanske reste han snabbt eller kanske mycket långsamt. För tillfället är det inte känt.

Medelhastigheten: en skalarnas storlek

Detta leder till att vi definierar en ny term: The Medelhastighet. I fysiken är det viktigt att skilja mellan vektorstorlekarna och storleken som inte är: skalarna.

För partikeln som gjorde tur och retur är medelhastigheten 0, men det kunde ha varit mycket snabbt eller kanske inte. För att veta det definieras medelhastigheten som:

Enheterna i medelhastigheten är desamma som med medelhastigheten. Den grundläggande skillnaden mellan båda storlekarna är att medelhastigheten innehåller intressant information om riktningen och riktningen för partikeln.

Det kan tjäna dig: fermioniskt kondensat: egenskaper, applikationer och exempel

Å andra sidan ger medelhastigheten endast numerisk information. Med henne är det känt hur snabbt eller långsamt partikeln rörde sig, men inte om han gjorde det framåt eller bakåt. Det är därför det är en skalär storlek. Hur man skiljer dem för att beteckna dem? Ett sätt är att lämna djärva för vektorer eller placera en pil på dem.

Och det är viktigt att notera att medelhastigheten inte behöver vara lika med medelhastigheten. För rundturen är medelhastigheten noll, men medelhastigheten gör det inte. Båda har samma numeriska värde när de alltid reser i samma riktning.

Träning löst

Du åker hem från skolan tyst på 95 km/h per 130 km. Börja regna och minska hastigheten till 65 km/h. Han kommer äntligen hem efter att ha kört i 3 timmar och 20 minuter.

a) Hur långt är ditt skolhem?

b) Vad var medelhastigheten?

Svar:

a) Vissa tidigare beräkningar är nödvändiga:

Resan är uppdelad i två delar, det totala avståndet är:

D = d1+ d₂, Med D1 = 130 km

Den totala tiden är 3 timmar och 20 minuter = 3 + 1/3 timmar = 10/3 timmar = 3.33 timmar (det är nödvändigt att placera samma enheter för tid, i detta fall är det lämpligt).

T2 = 3.33 - 1.37 timmar = 1.96 timmar

Beräkning av D_2:

d₂ = 65 km/h x 1.96 H = 125. 4 km.

Skolan är d1+ d₂ = 255.4 km från huset.

b) Nu kan du hitta medelhastigheten:

Referenser

1. Giancoli, D. Fysik. Principer med applikationer. Sjätte upplagan. Prentice hall. 21-22.
2. Resnick, r. (1999). Fysisk. Volym 1. Tredje upplagan på spanska. Mexiko. Kontinentala redaktionella företag s.TILL. av C.V. 20-21.
3. Serway, R., Jewett, J. (2008). Fysik för vetenskap och teknik. Volym 1. 7ma. Utgåva. Mexiko. Cengage Learning Editors. 21-23.