Mekanisk fördelformel, ekvationer, beräkning och exempel

De Mekanisk fördel Det är den dimensionella faktorn som kvantifierar förmågan hos en mekanism att förstärka - i vissa fall minskar - kraften som utövas genom den. Konceptet tillämpas på vilken mekanism som helst: från sax till en sportbils motor.

Tanken är att en maskin transformerar kraften som användaren tillämpar på den i en mycket större kraft än som representerar fördel, eller minskar den för att utföra en delikat uppgift.

Figur 1. Den hydrauliska hissen är en maskin med mekanisk fördel större än 1. Källa: Pixabay.

Tänk på att när man agerar en mekanism investeras en del av den applicerade kraften oundvikligen i att motverka friktion. Det är därför den mekaniska fördelen klassificeras som verklig mekanisk fördel och idealisk mekanisk fördel.

[TOC]

Definition och formler

Den verkliga mekaniska fördelen med en maskin definieras som orsaken mellan storleken på kraften som utövas av maskinen på lasten (utgångskraft) och kraften som krävs för att använda maskinen (ingångskraft):

Verklig mekanisk fördel VMR = utgångskraft/ingångskraft

Medan den ideala mekaniska fördelen beror på avståndet som går genom ingångskraften och den som går genom utgångskraften:

Idealisk mekanisk fördel vmi = ingångsavstånd/utgångsavstånd

Att vara kvoter mellan mängder med samma dimensioner, båda fördelarna är dimensionlösa (utan enheter) och också positiva.

I många fall, såsom lastbilen och hydraulisk press, är den mekaniska fördelen större än 1, och i andra är den mekaniska fördelen mindre än 1, till exempel i fiskekör och pincett.

Idealisk VMI -mekanisk fördel

VMI är relaterat till det mekaniska arbete som utförs vid ingången och vid utgången av en maskin. Arbetet vid ingången, som vi kommer att kalla w_Yo, Det är uppdelat i två komponenter:

Kan tjäna dig: Doppler -effekt: Beskrivning, formler, fall, exempel

W_Yo = Arbete för att övervinna friktion + utgångsarbete

En idealisk maskin behöver inte göra arbete för att övervinna friktion, därför skulle ingångsarbetet vara detsamma som utgången, betecknad som W_antingen:

Arbeta vid ingången = arbeta vid utgången → W_Yo = W_antingen.

Eftersom i detta fall arbetet är styrka efter avstånd har du: W_Yo = F_Yo . s_Yo

Där f_Yo och s_Yo Den ursprungliga kraften och avståndet är respektive. Utgångsarbetet uttrycks analogt:

W_antingen= F_antingen . s_antingen

I detta fall f_antingen och s_antingen är styrkan och avståndet som maskinerna levererar respektive. Nu matchas båda verken:

F_Yo . s_Yo = F_antingen . s_antingen

Och resultatet kan skrivas om i form av kvoter för krafter och avstånd:

(s_Yo /s_antingen) = (F_antingen /F_Yo)

Exakt är avståndskvoten den ideala mekaniska fördelen, enligt definitionen som anges i början:

Vmi = s_Yo /s_antingen

Effektivitet eller maskinprestanda

Det är rimligt att tänka på effektiviteten i omvandlingen mellan båda verken: ingången och utgången. Betecknar hur och För effektivitet definieras detta som:

E = utgångsarbete /ingångsarbete = W_antingen /W_Yo = F_antingen . s_antingen / F_Yo . s_Yo

Effektivitet kallas också mekanisk prestanda. I praktiken överskrider utgångsarbetet aldrig ingången på grund av friktionsförluster, därför kvoten som ges av och Det är inte längre lika med 1, men mindre.

En alternativ definition involverar kraft, vilket är det arbete som gjorts per tidsenhet:

E = utgångseffekt /ingångseffekt = P_antingen /P_Yo

Verklig mekanisk fördel VMR

Den verkliga mekaniska fördelen definieras helt enkelt som förhållandet mellan utgångskraften f_antingen och ingången f_Yo:

Vmr = f_antingen/F_Yo

Förhållandet mellan VMI, VMR och effektivitet

Effektivitet och Det kan skrivas om i termer av VMI och VMR:

Kan tjäna dig: termisk dilatation

e = f_antingen . s_antingen / F_Yo . s_Yo  = (F_antingen /F_Yo).(s_antingen/s_Yo) = VMR /VMI

Därför är effektiviteten kvoten mellan verklig mekanisk fördel och idealisk mekanisk fördel, som är den första lägre än den andra.

VMR -beräkning Knowing Effektivitet

I praktiken beräknas VMR genom att bestämma effektiviteten och känna till VMI:
VMR = E. Vmi

Hur beräknas mekanisk fördel?

Beräkningen av mekanisk fördel beror på maskinens typ. I vissa fall är det bekvämt att transportera den genom överföringen av krafterna, men i andra typer av maskiner, till exempel remskivor är det vridmomentet eller vridmomentet τ vad som överförs överförs.

I detta fall beräknas VMI genom att matcha ögonblicken:

Utgång torsionsmoment = inmatning torsionsmoment

Momentets storlek är τ = f.r.synd θ. Om kraften och positionsvektorn är vinkelrätt, finns det en vinkel på 90º och SEN θ = SEN 90º = 1, erhåller:

F_antingen . r_antingen = F_Yo . r_Yo

I mekanismer som den hydrauliska pressen, som består av två kameror som är sammankopplade med ett tvärgående rör och fullt av en vätska, kan tryck överföras av kolvar som rör sig fritt i varje kammare. I så fall beräknas VMI av:

Utgångstryck = tryck i ingången

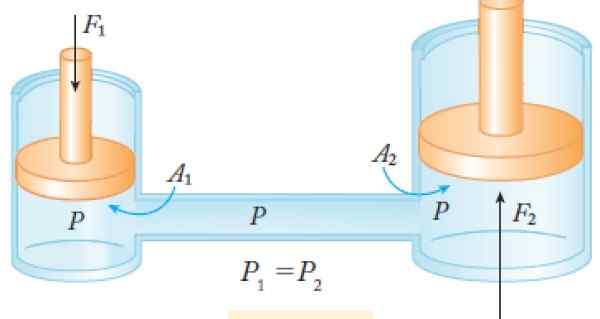figur 2. Hydraulisk pressprogram. Källa: Cuéllar, J. 2015. Fysik II. McGraw Hill.

Exempel

- Exempel 1

Spaken består av en tunn stång som stöds av ett stöd som heter Fulcro, som kan placeras på flera sätt. När man applicerar en viss kraft, kallad "maktkraft", löper den ut med en mycket större, vilket är börda antingen uthållighet.

Figur 3. Förstklassspak. Källa: Wikimedia Commons. CR [CC BY-S (http: // Creativecommons.Org/licenser/BY-SA/3.0/]]

Det finns flera sätt att hitta stöd, kraftkraften och belastningen för att uppnå en mekanisk fördel. Figur 3 visar den första klassspaken, liknande en vippare, med huvudkretsen som ligger mellan kraftkraften och belastningen.

Kan tjäna dig: Oblique Parabolic Shot: Egenskaper, formler, ekvationer, exempel

Till exempel kan två personer med olika vikt vara i balans i vippan eller upp och ner Om de sitter på adekvata avstånd från Fulcro.

För att beräkna VMI i den första gradsspaken, eftersom det inte finns någon översättning eller friktion, men rotation matchas ögonblicken, och vet att båda krafterna är vinkelräta mot baren. Här f_Yo är kraftkraften och f_antingen Det är belastningen eller motståndet:

F_antingen . r_antingen = F_Yo . r_Yo

F_antingen /F_Yo  = r_Yo / r_antingen

Per definition vmi = f_antingen /F_Yo , så:

Vmi = r_Yo / r_antingen

I frånvaro av friktion: VMI = VMR. Observera att VMI kan vara större än eller mindre än 1.

- Exempel 2

Den ideala mekaniska fördelen med den hydrauliska pressen beräknas genom trycket, som enligt Pascal -principen överförs helt till alla punkter på vätskan som är begränsade i behållaren.

Ingångskraften f₁ I figur 2 appliceras den i den lilla kolven i området på₁ till vänster och utgångskraften f₂ Det erhålls i den stora kolven i området a₂ till höger. Så:

Ingångstryck = utgångstryck

Trycket definieras som kraft per enhetsenhet, därför:

(F₁ Till₁) = (F₂ Till₂) → A₂ Till₁  = F₂ / F₁ 

Eftersom VMI = F₂ / F₁, Du har den mekaniska fördelen genom kvoten mellan områdena:

Vmi = a₂ Till₁

Tycka om₂ > A₁, VMI är större än 1 och pressens effekt är att multiplicera kraften som appliceras i den lilla kolven f₁.

Referenser

1. Cuéllar, j. 2009. Fysik II. Första. Utgåva. McGraw Hill.
2. Kane, J. 2007. Fysisk. 2: a. Utgåva. Redaktör.
3. Tippens, s. 2011. Fysik: koncept och applikationer. Sjunde upplagan. McGraw Hill
4. Wikipedia. Spak. Återhämtad från: är.Wikipedia.org.
5. Wikipedia. Mekanisk fördel. Återhämtad från: är.Wikipedia.org.