Vågsamplitudegenskaper, formler och träning

De Vågamplitud Det är den maximala förskjutningen som upplever en punkt i en våg med avseende på jämviktspositionen. Vågorna manifesteras överallt och många sätt i världen runt oss: i havet, i ljudet och i repet av ett instrument som producerar det, i ljuset, på jordens yta och mycket mer.

Ett sätt att producera vågor och studera dess beteende är att observera vibrationen i ett rep som har ett fast slut. Genom att producera en störning i andra änden, överförs varje partikel i repet och med den störningen av störningen i form av en följd av pulser hela tiden.

Vågor manifesteras på många sätt i naturen. Källa: Pixabay.

När energin sprider sig antar repet som är tänkt att vara perfekt elastiskt, den typiska sinusformade formen med åsar och dalar som visas i figuren som visas nedan i följande avsnitt.

[TOC]

Egenskaper och betydelse av vågamplitud

Amplituden A är avståndet mellan vapen och referensaxel eller nivå 0. Om det föredras, mellan en dal och referensaxeln. Om störningen i repet är mild är amplituden A liten. Om störningen är intensiv kommer amplituden att bli större.

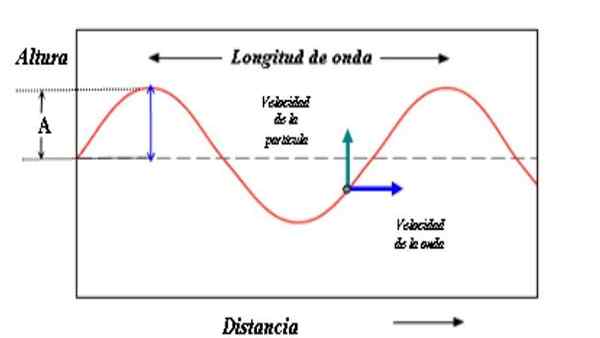En modell för att beskriva vågen består av en sinusformad kurva. Vågamplitud är avståndet mellan en vapen eller dal och referensaxeln. Källa: Paco [CC BY-SA 3.0 (http: // Creativecommons.Org/licenser/BY-SA/3.0/]]

Värdet på amplituden är också ett mått på energin som bär vågen. Det är intuitivt att stor amplitud är associerad med större energier.

I själva verket är energin proportionell mot kvadratet för amplituden, som uttryckt matematiskt är:

Jag ∝A²

Kan tjäna dig: ömsesidig induktans: formel/koefficient, applikationer, övningar

Där jag är vågens intensitet, i sin tur relaterad till energi.

Den typ av våg som produceras i exemplet rep, tillhör kategorin mekaniska vågor. En viktig egenskap är att varje partikel på repet alltid förblir mycket nära dess jämviktsposition.

Partiklarna rör sig inte eller rör sig genom repet. De sträcker sig upp och ner. Detta indikeras i toppschemat med den gröna pilen, men vågen tillsammans med dess energi, reser från vänster till höger (blå pil).

Vågor som sprids i vattnet ger nödvändiga bevis för att övertyga sig om detta. Att observera rörelsen av ett ark som har fallit i ett damm kan man se att hon helt enkelt svänger åtföljande av vattnet. Det går inte så långt, åtminstone klart, att det finns andra krafter som ger andra rörelser.

Vågmodellen som visas i figuren består av ett repetitivt mönster där avståndet mellan två åsar är våglängd λ. Om du vill, skiljer våglängden också två identiska punkter från vågen, även om de inte är på vapen.

Den matematiska beskrivningen av en våg

Naturligtvis kan vågen beskrivas med en matematisk funktion. Periodiska funktioner som sinus och kosinus är idealet för uppgiften, oavsett om du vill representera vågen både i rymden och i tid.

Om vi ​​kallar den vertikala axeln i figuren och den horisontella axeln vi kallar det "T", uttrycks vågens beteende över tid av:

y = a cos (ωt + Δ)

För denna ideala rörelse svänger varje reppartikel med enkel harmonisk rörelse, som härstammar tack vare en kraft som är direkt proportionell mot den förskjutning som görs av partikeln.

Kan tjäna dig: Dirac Jordan Atomic Model: Egenskaper och postulat

I den föreslagna ekvationen är a, ω och Δ parametrar som beskriver rörelsen, som är till amplitud tidigare definierat som den maximala förskjutningen som upplevs av partikeln med avseende på referensaxeln.

Kosinus argument kallas Rörelsefas Och Δ är faskonstant, Vad är fasen när t = 0. Både kosinusfunktionen och sinusfunktionen är lämpliga för att beskriva en våg, eftersom de bara skiljer sig från varandra π/2.

Det är vanligtvis möjligt att välja t = 0 med Δ = 0 för att förenkla uttrycket, erhålla:

y = a cos (ωt)

När rörelsen är repetitiv i både rum och tid finns det en karakteristisk tid som är period t, definieras som den tid det tar för partikeln att utföra en fullständig svängning.

Vågbeskrivning i tid: Karakteristiska parametrar

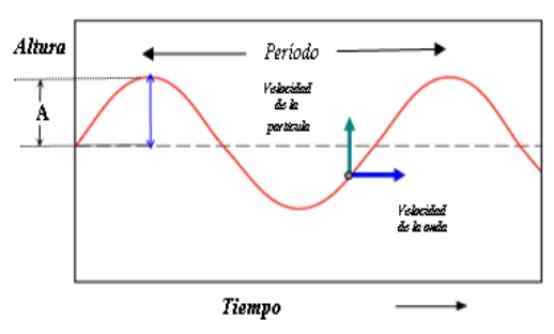Denna figur visar vågbeskrivningen i tid. Avståndet mellan åsar (eller dalar) motsvarar nu vågperioden. Källa: Paco [CC BY-SA 3.0 (http: // Creativecommons.Org/licenser/BY-SA/3.0/]]

Nu upprepar både bröstet och kosinuset dess värde när fasen ökar i värdet 2π, så att:

ωt = 2π → ω = 2π /t

Ω kallas rörelsefrekvens Och det har dimensioner av tidens omvända, att vara dess enheter i det internationella systemet radián / andra eller andra^-1.

Äntligen kan du definiera Rörelsefrekvens F, som periodens omvända eller ömsesidiga. Representerar i antalet åsar per tidsenhet, i vilket fall:

F = 1/t

Ω = 2πf

Både F och ω har samma dimensioner och enheter. Förutom den andra^-1, som kallas Hertz eller Hertzio, det är vanligt att höra om Varv per sekund antingen varv per minut.

Våghastighet v, som måste betonas att det inte är detsamma som den som upplevs av partiklarna, det kan enkelt beräknas om våglängden λ och frekvens f är kända:

Det kan tjäna dig: lysande kroppar: egenskaper och hur de genererar sitt eget ljus

V = λf

Om den svängning som upplever av partiklarna är av den enkla harmoniska typen, beror vinkelfrekvensen och frekvensen endast av arten av de oscillerande partiklarna och systemets egenskaper. Vågens amplitud påverkar inte dessa parametrar.

Till exempel, när du spelar en musikalisk anteckning på en gitarr, kommer anteckningen alltid att ha samma ton även om den berörs med större eller mindre intensitet, på detta sätt kommer en do alltid att låta som en do, även om den hörs starkare eller mjukare i en komposition, antingen på ett piano eller på en gitarr.

I naturen dämpas vågor som transporteras i en materiell miljö i alla riktningar eftersom energin försvinner. Av denna anledning minskar amplituden med det omvända avståndet r till källan, att vara möjlig att bekräfta det:

A∝1/r

Träning löst

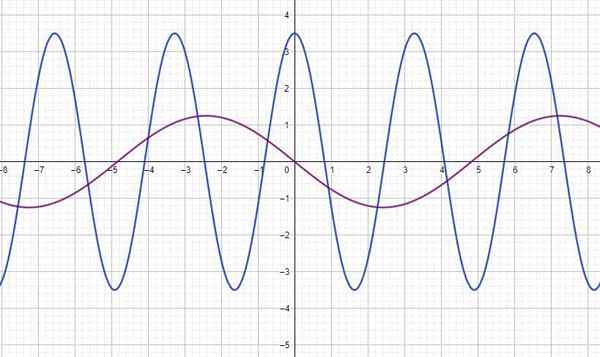
Figuren visar funktionen y (t) för två vågor, var och är i meter och t inom sekunder. För var och en hittar:

a) Amplitud

b) period

c) frekvens

d) Ekvationen för varje våg när det gäller bröst eller kosenos.

Svar

a) Det mäts direkt från grafen med hjälp av rutnätet: blå våg: a = 3.5m; Fuchsia Wave: A = 1.25 m

b) Den läser också grafen och bestämmer separationen mellan två toppar eller dalar, på varandra följande: blå våg: t = 3.3 sekunder; Fuchsia wave t = 9.7 sekunder

c) Det beräknas att komma ihåg att frekvensen är periodens ömsesidiga: blå våg: f = 0.302 Hz; Fuchsia Wave: F = 0.103 Hz.

d) blå våg: y (t) = 3.5 cos (ωt) = 3.5 cos (2πf.t) = 3.5 cos (1.9t) m; Fuchsia våg: y (t) = 1.25 synd (0.65t) = 1.25 cos (0.65T+1.57)

Observera att fuchsia -vågen är föråldrad π/2 med avseende på blått, som är möjlig att representera den med en sinusfunktion. Eller fördrivna kosinus π/2.