Hur man får procenten? Exempel och övningar

Burk få en procentandel Med flera metoder. Du kan snabbt beräkna 10% av valfritt antal när du flyttar din decimal en position till vänster. Till exempel är 10% av 100 10; 10% av 1000 är 100.

Om du vill beräkna mer komplexa procentsatser som 36% av 25 eller 250% av 20, behövs andra metoder. För fall där 10% -systemet inte är tillämpligt kan följande metoder beaktas.

Figur 1. Rabatter med olika procentsatser. Hur mycket räddar vi varandra?. Källa: Pixabay.

Termprocenten betyder en viss del av hundra och hänvisar till den aritmetiska operationen som utförs för att hitta nämnda del. Till exempel 20% ("tjugo procent") läses i pesos, det betyder att 20 pesos är diskonterade för varje 100 pesos.

Procentandelen tjänar till att beräkna vilken del av det totala som representerar ett belopp. I detta fall tas summan till omfattningen av 100 och procentsatsen informerar hur mycket, baserat på dessa 100, är ​​den del som ska beräknas.

Låt oss se hur det görs med dessa exempel. För det första gör vi det i form av en bråk:

• 20% = 20/100
• 5% = 5/100
• 0,7% = 0,7 / 100
• 100% = 100/100

Observera att 100% är lika med 1. Men procentsatserna kan också skrivas decimal:

• 20% = 0,20
• 5% = 0,05
• 0,7% = 0,007
• 100% = 1,0

När procentandelen av ett visst antal uttrycks, helt enkelt Komma rör sig Av de nummer två till vänster. I procenten, proportionalitetsregel:

20% är 20 av 100 därför:

20% av 100 är 20, 20% av 200 är 40, 20% av 300 är 60, 20% av 50 är 10.

Allmän regel för 20 % av alla belopp

20% av x är x *(20/100) = x *0,2 = 0,2 *x

Denna regel kan enkelt utvidgas för att hitta någon annan procentandel som önskas. Låt oss se hur i följande avsnitt.

Träning löstes med formel för att beräkna N% 

En formel för att sammanfatta så snart som möjligt och snabbt beräkna alla procentandelar n är:

n % =(A * n)/100

Till exempel vill du beräkna 25% av 400

Sedan n = 25 och a = 400, vilket resulterar i (400*25)/100 = 100

Exempel

Vilken procentandel av 60 är 24?

Lösning

Det som begärs motsvarar att fråga vad som är N% av 60 som ger 24?

Vi föreslår den allmänna formeln:

60 * N / 100 = 24

Vi rensar n Med denna procedur:

-De 100 som delar upp i medlem iZiédo Av jämlikhet, gå till medlemmen höger multiplikation. 

-Och de 60 som multipliceras i medlemmen vänster Gå till medlemmen höger delande.

N = 24 *100/60 = 2400/60 = 240/6 = 6 *40/6 = 40

Det dras slutsatsen att 40% av 60 är 24.

Löst procentuella beräkningar 

Nedan följer enkla övningar för att börja öva på nämnda.

Det kan tjäna dig: de 15 mest populära legenderna och myterna

Övning 1

Hitta 50% av 90.

Lösning

Här x = 90, n = 50 % och byt ut:

90 * 50% = 90 * (50/100) = 4500 /100 = 45 

Detta är ganska enkelt, eftersom 50 % av alla belopp är hälften av det beloppet och hälften av 90 är 45.

Övning 2

Hitta 30% av 90.

Lösning

90 * 30% = 90 * (30/100) = 2700/100 = 27

Procentuell ökning

Det är ofta i vardagen att lyssna på ökningen av något, till exempel en ökning av produktionen, en löneförhöjning eller ökningen av en produkt. Det uttrycks nästan alltid i procentform.

Till exempel kostade en viss produkt 300 € men fick en ökning med 30%. Vi frågar oss själva: vad är det nya produktpriset?

Den första är att beräkna den del som motsvarar ökningen. Eftersom ökningen är 30 delar av 100, så ökningen av ökningen, baserat på det ursprungliga priset på 300, är ​​tre gånger de 30 delarna, det vill säga 3*30 = 90.

Produkten ökade € 90, så det nya slutpriset kommer att vara vad som kostar ökningen innan:

Nytt pris = gammalt pris + € 90 = 390 €

Vi kan bygga en formel för beräkningen av den procentuella ökningen. Vi använder brev för att symbolisera priser, så här:

-F är det slutliga värdet

-Yo är initialvärdet och

-n är ökningen av ökningen.

Med dessa namn skulle det slutliga värdet beräknas så här:

f = i + (i* n / 100)

Men hur Yo Det upprepas i båda termerna, det kan tas som en vanlig faktorFör att få detta andra uttryck, lika giltigt:

F = i * (1 + n / 100)

Låt oss verifiera med fallet som redan har lösts, produkten som kostade 300 € och ökade 30%. Således ser vi till att formeln fungerar bra:

Slutpris = F = € 300 * (1 + 30/100) = € 300 * (1 + 0,3) = € 300 * 1,3 = € 390

Övning 3

En anställd tjänade 1500 €, men befordrades och hans lön hade en ökning med 20%. Vad är din nya lön?

Lösning

Låt oss tillämpa formeln:

F = € 1500 * (1 + 20/100) = € 1500 * (1 + 0,2) = € 1500 * 1.2 = € 1800

Den nya anställdslönen är 1800 €.

Procentuell minskning

När det gäller minskningar, formeln för beräkningen av det slutliga värdet F av ett visst initialt belopp Yo som fick en minskning av n% är:

F = i * (1 - n / 100)

Det bör noteras att det positiva tecknet (+) för formeln i föregående avsnitt ersattes av ett negativt tecken (-).

figur 2. Procentuell rabattmeddelande. Källa: Pixabay

Övning 4

En produkt märkt 800 €, men fick 15% rabatt. Vad är det nya produktpriset?

Lösning 4

Det slutliga priset enligt formeln är:

F = € 800 * (1 - 15/100) = € 800 * (1 - 0,15) = € 800 * (0,85) = € 680

Det slutliga priset med 15% rabatt är 680 €, vilket representerar en besparing på 120 €.

På varandra följande procentsatser

Det verkar när en viss mängd lider av en procentuell variation och sedan tillämpas en annan, också en procentandel. Till exempel en produkt som har haft två procentuella rabatter i rad. Ett annat exempel är en anställd som hade två löneförhöjningar i rad.

Kan tjäna dig: viktigare Yucatan ekonomiska aktiviteter

- Successiva procentuella ökningar

Lösningsbasen för dessa fall är densamma som de unika ökningarna, men den måste beaktas att den andra procentuella ökningen utförs på det slutliga värdet av den första ökningen.

Anta en produkt som steg upp 10% och sedan 5%. Det är felaktigt att säga att det fick en ökning med 15%, det var faktiskt mer än denna procentandel.

Formlerna för det slutliga värdet skulle gälla så här:

-Först beräknas det slutliga värdet på den första ökningen av N1%

f1 = i + i * n1 / 100

-Och sedan, för att hitta det slutliga värdet på den andra ökningen av N2%, tas det slutliga värdet på F1 som ett initialvärde. Därför:

F2 = F1 + F1 * N2 /100 

Övning 5

En bok kostade ursprungligen 55 €, men på grund av dess framgång och hög efterfrågan fick den två ökningar på det ursprungliga priset på det ursprungliga priset. Den första ökningen var 10% och den andra av 20%. Vad är det slutliga priset på boken?

Lösning

-Första ökningen:

F1 = € 55 * (1 + 10/100) = € 55 * 1,1 = € 60,5

-Andra ökningen

F2 = € 60,5 * (1 + 20/100) = € 60,5 * 1,2 = € 72,6

Det slutliga priset är 72,6 €.

Övning 6

Med hänvisning till den tidigare övningen. De två på varandra följande ökar: till vilken procentandel av en unik ökning jämfört med det ursprungliga bokpriset motsvarar?

Lösning

Om vi ​​kallar N% till procentandelen unik ökning, är formeln som relaterar denna unika procentuella ökning till det ursprungliga värdet och det slutliga värdet:

F2 = i *(1 + n / 100) 

Det vill säga:

72,6 € = € 55 + 55 € * (n / 100)

Rensa ökningen av ökningen n% = (n /100) har vi:

(N / 100) = (€ 72,6 - € 55) / 55 € = 17.€ 6 / € 55 = 0,32

Därför:

N = 0,32 * 100 = 32

Till priset på boken tillämpades en total procentuell ökning med 32%. Observera att denna ökning är större än summan av de två på varandra följande procentuella ökningarna.

- På varandra följande procentuella rabatter

Idén liknar den för successiva procentuella ökningar. Den andra procentuella rabatten måste alltid tillämpas på det slutliga värdet på den första rabatten, låt oss titta på ett exempel:

Övning 7

En rabatt på 10% följt av en andra rabatt på 20% på ett objekt, till vilken unik procentandel det är motsvarande?

Lösning

-Första rabatt:

F1 = i - i * n1 / 100  

-Andra rabatt

F2 = F1 - F1 * N2 / 100

Ersätta den första ekvationen i den andra kvarstår:

f2 = (i - i * n1 / 100) - (i - i * n1 / 100) * n2 / 100

Utveckla detta uttryck får vi:

F2 = i - i* n1 / 100 - i* n2 / 100 + i* (n1 / 100) (n2 / 100) 

Ritning av gemensam faktor Yo:

f2 = i * (1- n1% - n2% + n1% * n2%)

Slutligen ersätts de procentsatser som anges i frågan:

F2 = I * (1 - 10% - 20% + 10% * 20%) = I * (1 - 0,1 - 0,2 + 0,1 * 0,2)

f2 = i * (1 - 0,3 + 0,02) = i * (0,72) = i * (1 - 0.28) = i * (1 - 100/100) = i * (1 - 28%)

Med andra ord, successiva rabatter på 10% och 20% motsvarar en unik 28% rabatt.

Avancerade övningar

Låt oss prova dessa övningar bara när idéerna från de tidigare har varit tillräckligt tydliga.

Det kan tjäna dig: enkla och vackra geografiska omslag, omslag, bilder

Övning 8

Basen för en triangel mäter 10 cm och höjd 6 cm. Om baslängden minskar med 10%. I vilken procentandel ska höjden ökas så att triangelområdet inte förändras?

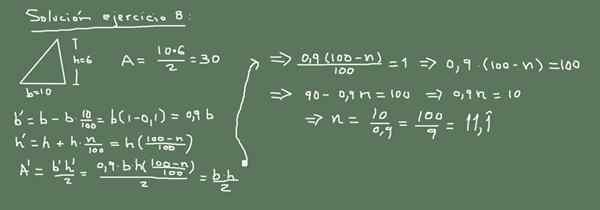Figur 3. Alternativ lösning på övning 8. Förberedd av f. Zapata.

Lösning 8

Det ursprungliga triangelområdet är:

A = (10 cm * 6 cm) / 2 = 30 cm²

Nu, om basen minskar med 10%, är dess nya värde:

Ny bas = 10 - (10/100) x 10 = 9 cm.

Det nya höjdvärdet kommer att vara x, och det ursprungliga området måste hållas oförändrat, så att:

(9cm * x) /2 = 30 cm²

Då rensas värdet på X:

X = 60 cm² / 9 cm = (20/3) cm = 6 666 cm

Vilket innebär en ökning med 0,666 jämfört med det ursprungliga värdet. Låt oss nu se vilken procentandel av detta som representerar:

6 666 = 6 + (6 * n/100) 

6 666 -6 = 6 * N/100

0.666 = 6 * N/100

N/100 = 0,111

N = 11.1

Svaret är: höjden måste ökas med 11,1% för att triangelområdet förblir detsamma.

Övning 9

Om lönen höjs med 20%, men sedan skatter 5%, vad är den verkliga ökningen som arbetaren får?

Lösning 

Först beräknar vi ökningen av N1%:

f1 = i + i * n1 / 100

Sedan tillämpar vi N2%rabatt:

F2 = F1 - F1 * N2 / 100

Den första ekvationen ersätts i den andra:

f2 = i + i * n1 / 100 - (i + i * n1 / 100) * n2 / 100

Det tidigare uttrycket utvecklas:

f2 = i + i * n1 / 100 - i * n2 / 100 - i * (n1 / 100) * (n2 / 100)

Slutligen tas det bort Yo Vanlig faktor och värdena på N1 = 20 och N2 = 5 som visas i uttalandet ersätts:

F2 = I (1 + 0,2 - 0,05 - 0,2* 0,05) = i* (1 + 7/50) = i* (1 + 14/100) = i* (1 + 14%)

Arbetaren fick en nettoökning på 14%.

Övning 10

Bestäm vad som är mest bekvämt mellan dessa två alternativ:

i) förvärva t -shirts med 32 % rabatt vardera.

Ii) Köp 3 t -skjortor till priset på 2.

Lösning 

Vi analyserar varje alternativ separat och väljer sedan det mest ekonomiska:

i) Låt X vara det nuvarande priset på en skjorta, en rabatt på 32 % representerar ett slutpris på XF:

Xf = x - (32/100) x = x - 0.32x = 0.68x

Att till exempel köpa 3 skjortor innebär att spendera 3 x 0.68 x = 2.04x

ii) Om x är priset på en skjorta, för 3 skjortor betalar du helt enkelt 2x.

Anta att en skjorta är värd 6 euro, med 32 % rabatt skulle det vara värt 4.08 euro. Köp 1 T -skjort är inte ett giltigt alternativ i erbjudandet 3 × 2. Så om du bara vill köpa en skjorta är rabatten att föredra.

Men om det du vill är att köpa för dussintals, är 3 × 2 -erbjudandet bara lite billigare. Till exempel skulle 6 t -skjortor med rabatten gå ut för 24.48 euro, medan de med 3 × 2 -erbjudandet skulle kosta 24 euro

Referenser

1. Lätt klassrum. Procenten. Hämtad från: klassrum.com
2. Baldor A. 2006. Praktisk teoretisk aritmetik. Kulturutgåvor.
3. Educa Kids. Hur man lär sig att beräkna procentsatser. Återhämtat sig från: Educapeques.com
4. Gutiérrez, g. Finansiella matematikanteckningar. Återhämtat sig från: CSH.Izt.Uam.mx
5. Smarta fästingar. Procentandel: Vad är och hur beräknas. Återhämtat sig från: smartick.är