Ojämlikhet i demonstrationstriangeln, exempel, övningar löst

Det kallas Ojämlikhet i triangeln till fastigheten som uppfyller två verkliga siffror som består av det absoluta värdet på dess summa är alltid mindre än eller lika med summan av dess absoluta värden. Den här egenskapen är också känd som Minkowski -ojämlikhet eller triangulär ojämlikhet.

Denna egenskap av siffrorna kallas triangulär ojämlikhet eftersom det i trianglarna händer att längden på ena sidan alltid är mindre än eller lika med summan av de andra två, även om denna ojämlikhet inte alltid gäller inom trianglar.

Figur 1. Det absoluta värdet på summan av två siffror är alltid mindre än eller lika med summan av dess absoluta värden. (Förberedd av R. Pérez)

Det finns flera demonstrationer av triangulär ojämlikhet i verkliga antal, men i detta fall kommer vi att välja en baserad på egenskaperna för det absoluta värdet och den fyrkantiga binomialen.

Sats: För alla par av siffror till och b Tillhör riktiga siffror måste det:

| A + B | ≤ | a | + | b |

[TOC]

Demonstration

Vi börjar med att överväga den första medlemmen i ojämlikheten, som kommer att skäras ner:

| A + B |^2 = (A + B)^2 = A^2 + 2 A B + B^2 (EC. 1)

I föregående steg har fastigheten använts att valfritt antal höga till torget är lika med det absoluta värdet på nämnda antal höga till torget, det vill säga: | x |^2 = x^2. Utvecklingen av torget binomial har också använts.

Allt nummer x Det är mindre än eller lika med dess absoluta värde. Om antalet är positivt är det värt jämlikhet, men om antalet är negativt kommer det alltid att vara mindre än ett positivt antal. I detta fall är det egna absoluta värdet, det vill säga att det kan anges det x ≤ | x |.

Kan tjäna dig: Icke -linjär programmering: Metoder och övningar

Produkten (a b) Det är ett nummer, därför tillämpas det (A B) ≤ | A B |. När den här egenskapen tillämpas på (EC. 1) Vi har:

| A + b |^2 = a^2 + 2 (a b) + b^2 ≤ a^2 + 2 | A B | + B^2 (EC. 2)

Med hänsyn till det | A B | = | A || b | La (EC. 2) Det kan skrivas enligt följande:

 | A + b |^2 ≤ a^2 + 2 | A || b | + B^2 (EC. 3)

Men som vi har sagt tidigare att kvadratet för ett nummer är lika med det absoluta värdet på antalet höga till torget, kan ekvation 3 skrivas om enligt följande:

 | A + b |^2 ≤ | a |^2 + 2 | a | | B | + | B |^2 (EC. 4)

I den andra medlemmen av ojämlikhet erkänns en anmärkningsvärd produkt, som när tillämpas leder till:

 | A + B |^2 ≤ (| A | + | B |)^2 (EC. 5)

I det tidigare uttrycket bör det noteras att värdena som ska höjas på båda medlemmarna i ojämlikhet också är positiva att det också måste uppfyllas att:

 | A + B | ≤ (| A |+ | B |) (EC. 6)

Det tidigare uttrycket är exakt vad du ville visa.

Exempel

Därefter kommer vi att kontrollera den triangulära ojämlikheten med flera exempel.

Exempel 1

Värdet tas A = 2 och värdet B = 5, det vill säga både positiva siffror och vi verifierar om ojämlikheten uppfylls eller inte.

 | 2 + 5 | ≤ | 2 |+ | 5 |

 | 7 | ≤ | 2 |+ | 5 |

7 ≤ 2+ 5

Jämställdhet verifieras, därför har triangelns ojämlikhetsteorem uppfyllts.

Exempel 2

Följande värden väljs a = 2 och b = -5, det vill säga ett positivt antal och det andra negativt, vi kontrollerar om ojämlikheten uppfylls eller inte.

Kan tjäna dig: trinomial

 | 2 - 5 | ≤ | 2 |+ | -5 |

 | -3 | ≤ | 2 |+ | -5 |

 3 ≤ 2 + 5

Ojämlikhet uppfylls, därför har den triangulära ojämlikhetssatsen verifierats.

Exempel 3

Värdet tas A = -2 och värdet B = 5, det vill säga ett negativt antal och det andra positivt, vi verifierar om ojämlikheten uppfylls eller inte.

 | -2 + 5 | ≤ | -2 |+ | 5 |

 | 3 | ≤ | -2 |+ | 5 |

 3 ≤ 2 + 5

Ojämlikhet verifieras, därför har satsen uppfyllts.

Exempel 4

Följande värden A = -2 och B = -5 väljs, det vill säga både negativa siffror och vi kontrollerar om ojämlikhet är uppfyllda eller inte.

 | -2 - 5 | ≤ | -2 |+ | -5 |

 | -7 | ≤ | -2 |+ | -5 |

 7 ≤ 2+ 5

Jämställdhet verifieras, därför har Minkowsk -ojämlikhetsteoremet uppfyllts.

Exempel 5

Värdet tas A = 0 och värdet B = 5, det vill säga ett nollnummer och det andra positivt, sedan kontrollerar vi om ojämlikheten uppfylls eller inte.

 | 0 + 5 | ≤ | 0 |+ | 5 |

 | 5 | ≤ | 0 |+ | 5 |

 5 ≤ 0+ 5

Jämställdhet uppfylls, därför har triangelens ojämlikhetsteorem verifierats.

Exempel 6

Värdet tas A = 0 och värdet B = -7, det vill säga ett nollnummer och det andra positivt, sedan kontrollerar vi om ojämlikheten uppfylls eller inte.

 | 0 - 7 | ≤ | 0 |+ | -7 |

 | -7 | ≤ | 0 |+ | -7 |

 7 ≤ 0+ 7

Jämställdhet verifieras, därför har den triangulära ojämlikhetssatsen uppfyllts.

Löst övningar

I följande övningar representerar geometriskt ojämlikheten i triangeln eller ojämlikheten i Minkowski för siffror A och B.

Kan tjäna dig: papomudas

Numret A kommer att representeras som ett segment på X -axeln, dess ursprung eller sammanfaller med nollet på X -axeln och den andra änden av segmentet (vid punkt P) kommer att vara i positiv riktning (till höger) x axel om a> 0, men till < 0 estará hacia la dirección negativa del eje X, tantas unidades como indique su valor absoluto.

På liknande sätt kommer nummer B att representeras som ett segment vars ursprung är på punkt P. Den andra änden, det vill säga poängen som kommer att vara till höger om P om B är positiv (B> 0) och punkten Q kommer att vara | B | enheter till vänster om p om b<0.

Övning 1

Representera grafiskt ojämlikheten i triangeln för A = 5 och B = 3 | A + B | ≤ | a | + | b |, varelse C = a + b. 

Lösning 1: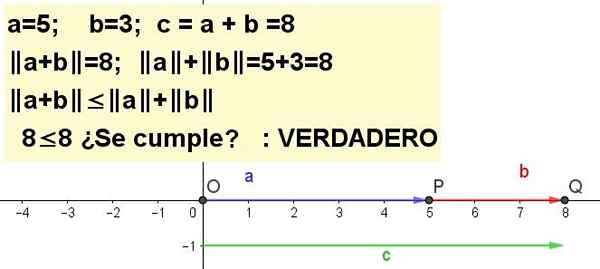

Övning 2

Gör en triangulär ojämlikhetsgraf för A = 5 och B = -3. 

| A + B | ≤ | a | + | b |, varelse C = a + b.

Lösning 2:

Övning 3

Grafera ojämlikheten i triangeln för A = -5 och B = 3.

| A + B | ≤ | a | + | b |, varelse C = a + b. 

Lösning 3: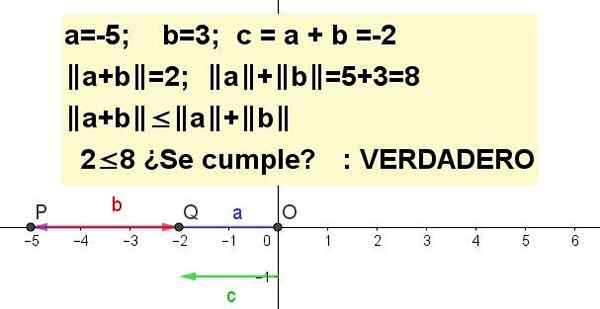

Övning 4

Graf den triangulära ojämlikheten för A = -5 och B = -3.

| A + B | ≤ | a | + | b |, varelse C = a + b.

Lösning 4: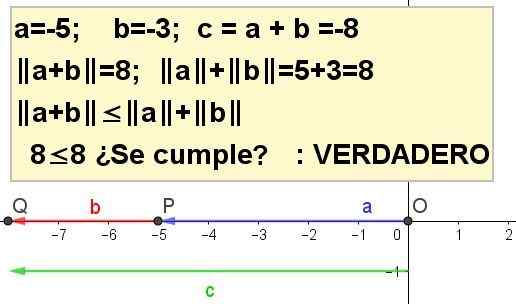

Referenser

1. OCH. Whitesitt. (1980).Booleska algebra och dess tillämpningar . Kontinentala redaktionella företag c. TILL.
2. Mícheal eller 'searcoid.(2003) Delar av abstrakt analys ... Department of Mathematics. University College Dublin, Beldfield, Dublind.
3. J. Van. (2006) Matematik och teknik inom datavetenskap. Institute for Computer Sciences and Technology. National Bureau of Standards. Washington, D. C. 20234
4. Eric Lehman. Matematik för datavetenskap.  Google Inc.
5. F Thomson Leighton (1980). Kalkyl. Institutionen för matematik och datavetenskap och AI -laboratorium, Massachussetts Institute of Technology.
6. Khan akademin. Triangel ojämlikhetsteorem. Återhämtat sig från: Khanacademy.org
7. Wikipedia. Triangulär ojämlikhet. Återhämtad från: är. Wikipedia.com