Diameter symboler och formler, hur man tar ut det, omkrets

han diameter Det är den raka linjen som passerar genom mitten av en stängd platt kurva eller en figur i två eller tre dimensioner och som också går med i motsatta punkter. Det är vanligtvis en cirkel (en platt kurva), en cirkel (en platt figur), en sfär eller en rak cirkulär cylinder (tre -dimensionella föremål).

Även om omkrets och cirkel vanligtvis tas som synonymer, finns det en skillnad mellan båda termerna. Omkretsen är den stängda kurvan som omsluter till cirkeln, som uppfyller villkoret att avståndet mellan någon av dess punkter och centrum är detsamma. Detta avstånd är ingen annan än omkretsens radie. Istället är cirkeln en platt figur begränsad av omkretsen.

Figur 1. Diametern på cykelhjulen är en viktig funktion i dess design. Källa: Pixabay.

Vid omkrets, cirkel och sfär är diametern ett rak segment som innehåller minst tre punkter: mitten plus två punkter på kanten av omkretsen eller cirkeln, eller ytan på sfären.

Och när det gäller den raka cirkulära cylindern hänvisar diametern till tvärsnittet, som tillsammans med höjden är dess två karakteristiska parametrar.

Omkretsens diameter och cirkeln, symboliserad av Ø eller helt enkelt bokstaven "D" eller "D", är relaterad till dess omkrets, kontur eller längd, som betecknas med bokstaven L:

L = π.D = π. antingen

När du har en omkrets är kvoten mellan dess längd och dess diameter det irrationella antalet π = 3.14159 ..., på detta sätt:

π = l/d

[TOC]

Hur man får diametern?

När ritningen av omkretsen eller cirkeln är tillgänglig, eller direkt det cirkulära objektet, till exempel en valuta eller en ring till exempel, är det mycket lätt att ta diametern med en regel. Du måste helt enkelt se till att kanten på regeln samtidigt har två punkter i omkretsen och mitten av samma.

Kan tjäna dig: algebraisk

En kaliber, vernier eller kungens fot är mycket lämplig för att mäta externa och inre diametrar i mynt, bågar, ringar, nötter, rör och mer.

figur 2. Vernier Digital mäter diametern på ett mynt. Källa: Pixabay.

Om du istället för objektet eller dess ritning har data som radion R, Sedan multiplicerar du med 2 du har diametern. Och om omkretsens längd eller omkrets är känd, kan diametern också vara känd, genom clearance:

D = 2.R
D = l / π

Ett annat sätt att få diametern är att känna till cirkelområdet, den sfäriska ytan, cylinderns tvärsnitt, det böjda området för detta eller volymerna på sfären eller cylindern. Allt beror på vilken geometrisk figur som är det. Till exempel är diametern involverad i följande områden och volymer:

-Cirkelområde: π.(D/2)²
-Sfärisk ytan: 4π.(D/2)²
-Sfärvolym: (4/3) π.(D/2)³
-Rak cirkulär cylindervolym: π.(D/2)².H (H är cylinderhöjden)

Figurer av konstant bred

Cirkeln är en platt figur av konstant bred, eftersom var den ser ut, bredden är diameter D. Det finns emellertid andra kanske mindre kända figurer vars bredd också är konstant.

Låt oss först se vad som förstås av en figurbredd: det är avståndet mellan två parallella linjer -Support Remes -som i sin tur är vinkelrätt mot den givna riktningen och som fängslar figuren, som visas i den vänstra bilden:

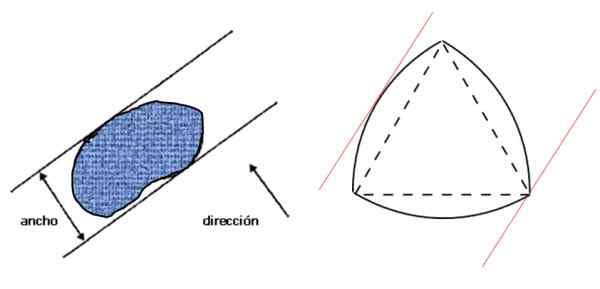Figur 3. Bredd på någon platt figur (vänster) och Reuleaux Triangle, en konstant bred figur (höger). Källa: f. Zapata.

Då till höger är Reuleaux -triangeln, som är en konstant bred figur och som uppfyller det tillstånd som anges i vänster figur. Om figurens bredd är d ges dess omkrets av Barbiers sats:

Kan tjäna dig: ungefärlig mätning av amorfa figurer: exempel och träning

L = π.D

Upploppet i staden San Francisco i Kalifornien är formade som Reuleauxs triangel, namngivna av den tyska ingenjören Franz Reuleaux (1829 - 1905). På detta sätt kan taporna inte falla ner i hålet och spendera mindre material för att tillverka dem, eftersom deras område är mindre än cirkeln:

A = (1- √3).πd² = 0.705.D²

Medan en cirkel:

A = π.(D/2)² = (π/4) D²= 0.785.D²

Men denna triangel är inte den enda konstanta breda figuren. Samtal kan byggas Reuleaux polygoner med andra polygoner som har ett udda sidorummer.

Omkretsens diameter

I nästa figur är elementen i omkretsen, definierade på följande sätt:

Rep: radsegment som förenar två punkter i omkretsen. I figuren är repet som går med i punkterna C och D, men oändliga strängar kan spåras som unika alla par omkretspunkter.

Diameter: Det är repet som passerar genom mitten och går med två punkter i omkretsen med mitten eller. Det är det längsta repet av en omkrets, av den anledningen kallas det "Major Rope".

Radio: linjesegment som ansluter sig till centrum med någon punkt i omkretsen. Dess värde, som diametern, är konstant.

Omkrets: Det är uppsättningen av alla punkter som motsvarar eller.

Rosett: Det definieras som ett omkretssegment avgränsat av två radioapparater (inte ritade i figuren).

Figur 4. Delar av omkretsen, inklusive diametern, som passerar genom mitten. Källa: Wikimedia Commons.

- Exempel 1

Rektangeln som visas mäter 10 tum hög, som vid lindring bildar en rak cirkulär cylinder vars diameter är 5 tum. Svara på följande frågor:

Det kan tjäna dig: ömsesidigt exklusiva evenemang: egenskaper och exempel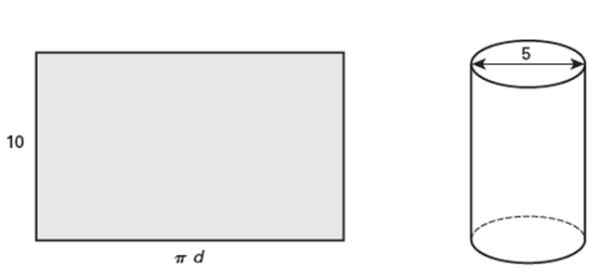Figur 5. En rullad rektangel blir en rak cirkulär cylinder. Källa: Jiménez, R. Matematik II. Geometri och trigonometri. 2: a. Utgåva. Pearson.

a) Vad är rörets kontur?
b) Hitta rektangelområdet
c) Beräkna cylinderns tvärsektionsarea.

Lösning till

Rörets kontur är l = π.D = 5π plg = 15.71 PLG.

Lösning B

Rektangelområdet är Bas x höjd, Att vara basen L redan beräknad och höjden är 10 PLG enligt uttalandet, därför:

A = 15.71 PLG x 10 PLG = 157.1 PLG².

Lösning C

Slutligen beräknas det begärda området enligt följande:

A = π.(D/2)² = (π/4) D² = (π/4) x (5 PLG)²= 19.63 PLG².

- Exempel 2

Beräkna det skuggade området i figur 5A. Torget har sida L.

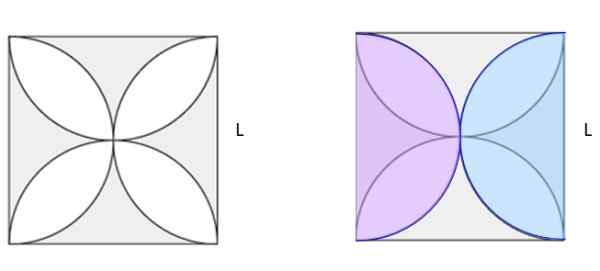Figur 6. Hitta det skuggade området i vänster figur. Jiménez, r. Matematik II. Geometri och trigonometri. 2: a. Utgåva. Pearson.

Lösning

I figur 5b har två identiska halvcirklar av storlek i rosa och blå färger ritats, överlagrats på den ursprungliga figuren. Mellan dem gör de en komplett cirkel. Om kvadratet på kvadratet beräknas och cirkelområdet subtraheras gör det det skuggade området i figur 5b. Och ser bra ut visar det sig att det är hälften av det skuggade området i 5A.

-Area Square: L²
-Semi -circle diameter: l
-Cirkelområde: π.(L/2)²= (π/4) l²
-Skillnad mellan områden = hälften av det skuggade området =

L² - (π/4) l² = [(4 - π)/4] l²= 0.2146 L²

-Skuggat område = 2 x 0.2146 L²= 0.4292L2

Hur många diametrar har en omkrets?

Oändliga diametrar kan dras i en cirkel, och någon av dem mäter samma.

Referenser

1. Antonio. Reuleaux -trianglar och andra konstant breddkurvor. Återhämtat sig från: disseminatorer.com.
2. Baldor, a. 2002. Flat och rymd- och trigonometri -geometri. Kulturhem.
3. Jiménez, r. Matematik II. Geometri och trigonometri. 2: a. Utgåva. Pearson.
4. Wikipedia. Reuleaux triangel. Återhämtat sig från: det är.Wikipedia.org.
5. Wolfram Mathworld. Diameter. Återhämtat sig från: Mathworld.Volfram.com.