Clausius-Clapeyron-ekvation Vad är det för, exempel, övningar
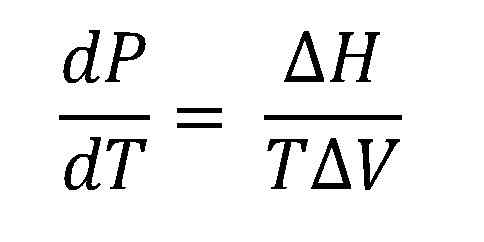
- 4369
- 363
- Erik Eriksson
De Clausius-Clapeyron-ekvation Det är en som relaterar förändringarna i ångtrycket och temperaturen, i en fas eller förändring av tillståndsövergången. Gäller sublimeringar, förångningar, sammanslagningar eller till och med förändringar i kristallina faser. Det är värt att nämna att denna ekvation gäller för ett rent ämne som är i jämvikt.
Denna ekvation härstammar från de termodynamiska lagarna och P-T-diagrammen för ett ämne, där samexistenslinjen observeras; Det som skiljer två olika faser (vätskevapor, fast-vätska, etc.). För att överföra denna linje är vinst eller förlust av värme nödvändig, såsom förångningsentalpi, ΔHVep.
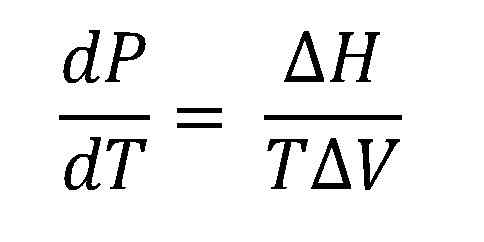 Clausius-Clapeyron-ekvation. Källa: Gabriel Bolívar.
Clausius-Clapeyron-ekvation. Källa: Gabriel Bolívar. Den högre bilden visar Clausius-Clapeyron-ekvationen innan den integreras. Normalt tillämpas det vanligtvis på vätskesystem, där ΔH användsVep och du vill beräkna vad vätskeprycket kommer att vara vid en viss temperatur. Det tjänar också till att beräkna ΔHVep av en viss vätska i ett temperaturområde.
Clausisu-clapeyron-ekvation används också ganska ofta för att studera tryckförändringar i flyktiga fasta ämnen; det vill säga sublimeringsentalpin övervägs, Δhsub.
[TOC]
Vad är Clausisu-Clapeyron-ekvationen för?
Beräkning av tryck på trycket och förångningsentalperna
Från ekvationen av Clausius-Clapeyron uppifrån görs äntligen några matematiska överväganden för att äntligen utföra en integration. För ett vätskevaporsystem antas till exempel att ΔHVep Det varierar inte med temperaturen, och att ΔV uteslutande motsvarar ångvolymen och föraktar vätskans volym (vånga-Vflytande = Vånga).
Förutsatt att ånga uppträder som en idealisk gas och integrering erhålls ekvationen av Clausius-Clapeyron-integrerad:
Kan tjäna dig: förångning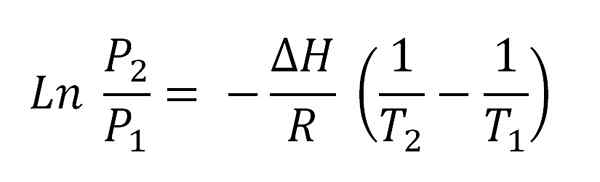 Clausius-Clapeyron-ekvation integrerad.
Clausius-Clapeyron-ekvation integrerad. Denna ekvation motsvarar den för en linje som är grafisk som:
Ln p vs 1/t
Och vars negativa lutning är (ΔH/r). För att uppfylla denna ekvation måste därför ΔH vara konstant i temperaturintervallet (t2-T1) där ångtryck mäts i jämvikt med vätskan.
På detta sätt, om det antas att ΔH varierar lite inom små temperaturintervall, är det möjligt att använda ekvationen för denna linje för att förutsäga förändringar i en vätskans ångtryck; Och ännu mer kan du bestämma dess ΔH för förångning.
Ju större temperaturintervaller beaktas, desto största avvikelse i denna ekvation av experimentella data, och desto mindre kommer den att uppfyllas.
Bestämning av fasförändringar
Således blir Clausius-Clapeyrons ekvation utvecklingen av en tangentlinje till samexistenslinjen mellan två fysiska faser, som observeras i alla P-T-diagram för ett ämne.
Om en fasändring inträffar kommer det att förändras i sluttningen och ΔH kommer inte att vara densamma. Därför, när starka avvikelser bevisas och ekvationen misslyckas, är det ett tecken på att ämnet i temperaturintervallet upplever en annan fasändring. Det vill säga det upphör att vara ett vätskevaporsystem, eftersom det överförs till samexistenslinjen som motsvarar den fasta vätskan eller solid -vaporbalanseringen.
Använd exempel
- Clausius-Clapeyron-ekvationen har använts i meteorologi för att studera molnens beteende, även de som finns på andra planeter eller månar med atmosfärer.
Kan tjäna dig: glukonsyra: struktur, egenskaper, syntes, användning- Det har använts för att bestämma fusionsentalpin för flera metaller såsom natrium och gallium och för att extrapolera deras ångtryck vid mycket höga temperaturer.
- Det har också använts för att bestämma entalpin av förångning av ämnen som gasformigt klor, koltetraklorid, flytande vatten, is och jod.
- Det har också tjänat till att studera fasförändringar i kristallina strukturer. I detta sista exempel ser Clausius-Clapeyrons integrerade ekvation anmärkningsvärt annorlunda ut, eftersom samma överväganden som tas för vätskevaporsystemet inte kan göras för ΔV. Volymvariationerna från en fas till den andra är små.
Löst övningar
- Övning 1
Isångtrycket är 4.58 Torr vid 0 ° C och 1.95 Torr A -10 ° C. Vad är din sublimeringsentalpi i det temperaturområdet?
Observera att vi har två tryck och två temperaturer:
P1 = 4.58 Torr
P2 = 1.95 Torr
T1 = 0 ° C + 273 = 273 K
T2 = -10 ° C + 273 = 263 K
Vi konverterar temperaturenheterna från ° C till K, eftersom den konstant R av gaser har k i dess enheter:
R = 8.314 j/k
Således använder vi den integrerade Clausius-Clapeyron-ekvationen och tydlig ΔHsub, Vilket skulle kvarstå som:
ΔHsub = -Rln (p2/P1) / (1 / t2 - 1 /t1)
För mer komfort kommer att fortsätta att ersätta endast med siffrorna, men att veta att den slutliga enheten kommer att vara Joule:
ΔHsub = -(8.314) ln (1.95/4.58)/(1/263 - 1/273)
= 50.97 J
Eller 51.07 J överväger några decimaler. Detta värde kommer att presentera svängningar beroende på intervall t2-T1 och av vissa ångtryck.
- Övning 2
Kokpunkten för etanol vid ett tryck av 760 torr (1 atm) är 78.3 ° C, och dess förångningsentalpi är 39.3 kJ. Vad är ditt ångtryck vid en temperatur av 46 ° C?
Det kan tjäna dig: tantalus: struktur, egenskaper, användningar, erhållningVi identifierar uppgifterna:
P1 = 760 Torr
P2 = ?
T1 = 78.3 ° C + 273 = 351.3 K
T2 = 46 ° C + 273 = 319 K
ΔHVep = 39.3 kJ eller 39300 j
Så vi måste rensa P2 av den integrerade Clausius-Clapeyron-ekvationen. Återigen kommer enheterna att utelämnas för komfort och beräkningarna kommer att utvecklas steg för steg:
Ln (p2/P1) = -(ΔHVep/R) (1/t2 - 1/t1)
Ln (p2/760) = -(39300/8.314) (1/319 - 1/351.3)
Ln (p2/760) = -1.36
Tillämpa den exponentiella funktionen på båda sidor av ekvationen för att kunna rensa p2 vi kommer att ha:
E (ln p2/760) = E(-1.36)
P2/760 = 0.256
P2 = 0.256 (760)
= 195 Torr
Vid en lägre temperatur (46 ° C), lägre ångtryck (195 Torr). Faktum är att ha etanolen ett tryck på 760 torr till 78.3 ° C, vi pratar om dess normala kokpunkt. Detta är det beteende som förväntas för alla vätskor
I allmänhet består Clausius-Clapeyron-övningar av denna typ av att rensa P2, T2 eller ΔH för förångning eller sublimering. Beräkningarna ändras avsevärt när ΔV också bör övervägas, särskilt när det gäller solid-vätskesystem eller balanser.
Referenser
- Whitten, Davis, Peck & Stanley. (2008). Kemi. (8: e upplagan.). Cengage Learning.
- Wikipedia. (2020). Clausius-Clapeyron-relation. Hämtad från: i.Wikipedia.org
- San José State University. (s.F.). Clausius-Clapeyron-ekvationen:
STIS -härledning och tillämpning i meteorologi. Återhämtat sig från: SJSU.Edu - Bodnergrupp. (s.F.). Clausius-Clapeyron-ekvationen. Hämtad från: Chemed.Kem.Purdu.Edu
- Chieh c. & Censulo a. (18 maj 2020). Clausius-Clapeyron-ekvation. Kemi librettexts. Återhämtad från: kem.Librettexts.org
- Walter J. Moore. (1962). Fysisk kemi. (Fjärde upplagan). Longmans.

