Kontinuitetsekvation

Vi förklarar vad som är kontinuitetsekvationen, dess formel, applikationer, exempel och föreslår övningar att lösa

Vad är kontinuitetsekvationen?

De Kontinuitetsekvation, För inkomprimerbar vätska fastställer den att den totala massan av en vätska som cirkulerar genom ett rör, utan förlust eller vinst, förblir konstant. Med andra ord bevaras degen utan förändringar när vätskan rör sig.

En inkomprimerbar vätska är den vars densitet förblir ungefär konstant under flödande. Till exempel är vatten en vätska som anses vara okomprimerbar under standardtryck och temperaturförhållanden.

Det finns ett matematiskt sätt att uttrycka bevarande av massan, i kontinuitetsekvationen, som ges av:

TILL₁∙ V₁ = A₂∙ V₂

Där v₁ och v₂ De representerar vätskans hastighet i två sektioner i ett rör, medan₁ redan₂ De är respektive tvärsektionsområden.

Produkten från tvärsektionsområdet med hastighet kallas flöde Och kontinuitetsekvationen innebär att flödet i hela röret är konstant. Flödet är också känt som volymflödeshastighet, Det förstås genom att noggrant observera det tidigare uttrycket, vars dimensioner är volym per tidsenhet.

Formel

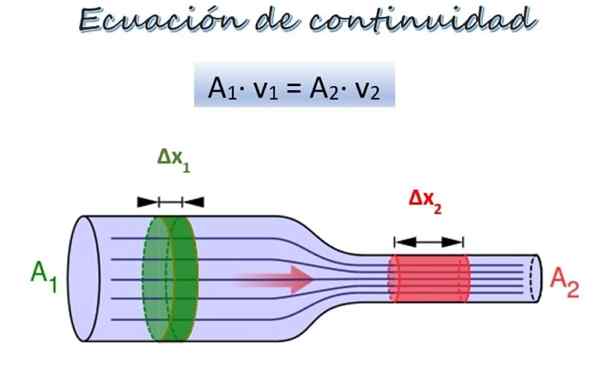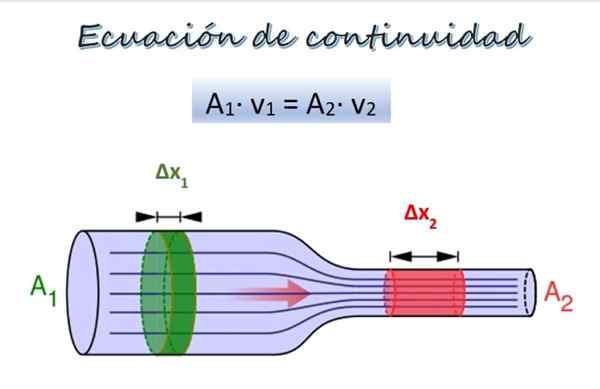
Kontinuitetsekvationen för flödet av en vätska längs ett rör med olika diametrar. Källa: Wikimedia Commons/F. Zapata.

I den övre bilden finns ett rör med två delar av olika diameter och i samma höjd, även om de kan vara i olika höjder utan att representera ett problem.

I avsnitt 1, bredare, är tvärsektionsområdet att₁ och vätskan rör sig med hastighet V₁, Medan i avsnitt 2, smalare, är tvärsektionsområdet att₂ och vätskans hastighet är v₂.

En degdel Δm₁ (grönt) rör sig efter avsnitt 1 i en tid ΔT. Under denna period₂ (röd) resa genom avsnitt 2. Eftersom vätskan är inkomprimerbar är dess densitet densamma i alla dess punkter, så från definitionen av densitet:

Det kan tjäna dig: Gase Constant: Vad är, beräkning och exempel

Här är ρ densitet, M är massa och V -volymen. Enligt detta är massan Δm₁ är lika med:

Δm₁ = ρ ∙ v₁

Där volym v₁ Det är produkten mellan tvärsnittet och avståndet Δx₁:

Δm₁ = ρ ∙ (a₁ ∙ Δx₁)

Men eftersom:

Sedan degdelen Δm₁ Du kan skriva, när det gäller hastighet och tid ΔT som:

Δm₁ = ρ ∙ a₁ ∙ Δx₁ = ρ ∙ a₁ ∙ (v₁ ∙ Δt)

Analog delen Δm är skriven₂ som flyter samtidigt efter avsnitt 2:

Δm₂ = ρ ∙ a₂ ∙ Δx₂ = ρ ∙ a₂ ∙ (v₂ ∙ Δt)

Genom att bevara massan:

Δm₁ = Δm₂

OCH:

ρ ∙ a₁ ∙ V₁ ∙ Δt = ρ ∙ a₂ ∙ V₂ ∙ ΔT

När ΔT och ρ avbryts, resultat:

TILL₁ ∙ V₁ = A₂ ∙ V₂

Flödet q

Produkten från tvärsnittet A med vätskans hastighet kallas flöde och betecknar som q. Det motsvarar volymen vätska per tidsenhet genom röret eller volymflödeshastigheten:

 V volym och Δt tidsintervallet. Flödeshastigheten i det internationella enhetssystemet är m³/s, även om kubikfot, gallon/min, gallon/s liter/s och gallon/s är ofta. Några av de mest använda omvandlingsfaktorerna är följande:

• 1 m³/S = 264.172 gal/s
• 1 l/s = 0.001 m³/s
• 1 ft³/S = 0.0283168 m³/s
• 1 l/s = 0,264172 gal/s
• 1 m³/S = 15850,3 gal/min

Observera att genom att minska rörets tvärsnitt ökar hastigheten på vätskan och vice versa, om tvärsnittet ökar, minskar hastigheten så att flödet är konstant.

Applikationer och exempel

Kontinuitetsekvationen används i analysen av vätskeflödet, i kombination med Bernoulli -ekvationen, där variationerna i vätskans hastighet i de olika sektionerna beaktas, liksom tryckförändringarna och effekten av höjd.

Kan tjäna dig: likström

Exempel 1

I familjens trädgårdsslang, när vattnet normalt lämnar strålen har ett visst intervall, men om det sätter fingret vid slangens utgång, vilket minskar utgångshålet, är jetens räckvidd större.

Här uppfylls kontinuitetsekvationen, eftersom genom att minska området för utgångsmunet ökar jetens hastighet så att hastighetsområdet med hastighet är konstant.

Exempel 2

Vattenstrålen minskar när den faller, eftersom hastigheten ökar. På detta sätt förblir produkthastigheten per område konstant

Ett annat exempel där kontinuitetsekvationen markeras är vattenstrålen som minskar när den faller på grund av ökningen av vattenhastigheten under hösten.

På detta sätt är flödet konstant, medan strålen fortsätter att flyta i en laminär regim, det vill säga att vattnet faller försiktigt utan turbulens eller virvlar.

Löst övningar

Övning 1

Vatten cirkulerar genom en 20 cm diameter rör. Att veta att flödet är 2000 l/s, hitta vattenhastigheten i röret.

• Lösning

Det är bekvämt att uttrycka allt i enheter i det internationella systemet. Först beräknas tvärsektionssektionen i röret, och kommer ihåg att radien är halva diametern:

A = π ∙ (d/2)²

D = 20 cm = 0.2 m

Därför är området:

A = π ∙ (d/2)² = A = π ∙ (0.2 m /2)² = 0.0314 m².

Flödet uttrycks i m³/s med hjälp av lämplig konverteringsfaktor:

Q = 2000 l/s = 2 m³/s

Från formeln q = a ∙ V hastigheten med vilken vätskan cirkulerar genom röret rensas:

Övning 2

Du har ett variabelt tvärsnittsrör genom vilket vatten flyter. Vid en viss tidpunkt är tvärsnittet 0.070 m² Och vattenhastigheten är 3.50 m/s. Beräkna:

Kan tjäna dig: Pascal Princip: Historia, Applications, Exempel

a) Hastigheten på vatten vid en annan punkt i röret vars tvärsnitt är 0.105 m².

b) Volymen av vatten som släpps ut av en öppen ände på 1 timme.

• Lösning till

Kontinuitetsekvationen används och matchar flödet av den första punkten med flödet av den andra. Flödet är:

Q = a ∙ v

För kontinuitet:

Q₁ = Q₂

TILL₁ ∙ V₁ = A₂ ∙ V₂

Nu ersätter de de uppgifter som tillhandahålls av uttalandet:

• TILL₁ = 0.070 m²
• v₁ = 3.50 m/s
• TILL₂ = 0.105 m²
• v₂ =?

Och rensar v₂:

Lösning B

Eftersom flödet också är volymen per tidsenhet måste det:

Därför är volym V:

V = q ∙ Δt = (a ∙ v) Δt

Flödet som kan beräknas med data från punkt 1 eller de i punkt 2, eftersom det är detsamma på båda punkterna:

Q = a₁ ∙ V₁ = 0.070 m² ∙ 3.50 m/s = 0.245 m³ / s

Att veta att 1 timme = 3600 s är volymen av vattenutladdning:

V = q ∙ Δt = (0.245 m³ / s) × (3600 s) = 882 m³

På 1 timme laddas 882 m³ vatten genom röret.