Allmän parabola -ekvation (exempel och övningar)

De Liknelsegenerad ekvation innehåller kvadratiska termer i x och i och, liksom linjära termer i båda variablerna plus en oberoende term. Den första symmetriaxeln är parallell med den vertikala axeln och den för den andra är den horisontella axeln.

I allmänhet den kvadratiska ekvationen som saknar den korsade termen Xy Det är skrivet som:

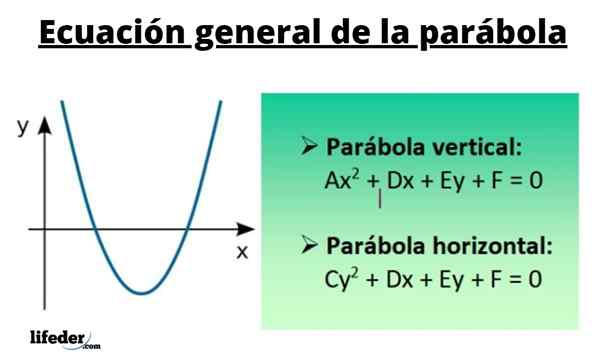
Yxa² + Cy² +Dx + ey + f = 0

Värdena på A, C, D, E och F är verkliga siffror. Att införa förhållandena vid ∙ C = 0 och A+C ≠ 0, kurvan som är resultatet av att grafera de punkter som tillfredsställer denna ekvation är en parabola.

Fall 1

För en vertikal liknelse är dess allmänna ekvation:

Yxa² + Dx + ey + f = 0

Där A och E skiljer sig från 0. Med andra ord, när en term visas med x², Liknelsen är vertikal.

Fall 2

För den horisontella liknelsen har du:

Cy² + Dx + ey + f = 0

Här skiljer sig c och d också från 0, därför motsvarar den kvadratiska termen och motsvarar och².

I alla fall är den allmänna ekvationen för liknelsen kvadratisk i en av variablerna och linjära i den andra.

Liknelselement

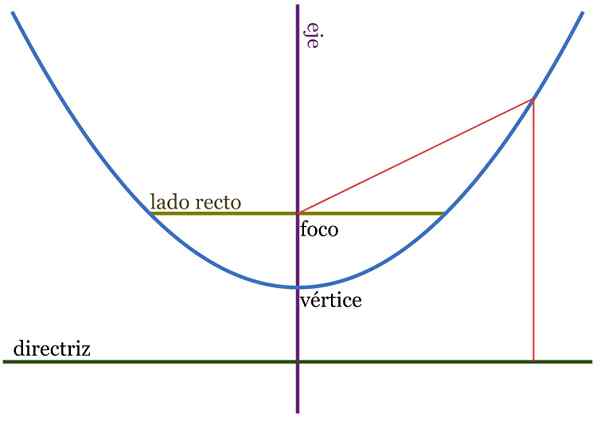figur 2. Liknelselement. Avståndet QF och QH är lika. Källa: Wikimedia Commons.

Parabolen, definierad som en geometrisk plats, består av uppsättningen punkter i ett plan som motsvarar en annan punkt som kallas fokus Och också av en linje, känd som rak riktlinje.

Från den allmänna ekvationen är det möjligt att studera liknelsen genom att specificera dess element. Inklusive fokus och riktlinjer, dessa element, som beskrivs kort är:

-Axel, som hänvisar till parabolens symmetriaxel, kan vara horisontellt (parallellt med Abscissas axel) eller vertikal (parallell med ordinatens axel).

Kan tjäna dig: Vanlig faktor för grupperingsvillkor: Exempel, övningar

-Orientering, som i sin tur motsvarar axelns orientering. Parabeln är vertikal om dess symmetriaxel är vertikal och den är horisontell när axeln också är.

-Vertex, Det är den punkt där axeln korsar liknelsen.

-Fokus, punkt belägen på axeln, inuti liknelsen och på avstånd p av toppen. Alla punkter i parabolen Equidist Fokus och riktlinjens riktning.

-Parameter, Det är avståndet p Mellan fokus och toppunkt.

-Rak riktlinje, som är vinkelrätt mot y -axeln och också ett avstånd p av liknelsens toppunkt, men korsar det inte, eftersom det är på utsidan.

-Rak sida, Det är repet som passerar genom fokus och korsar liknelsen i två punkter, vinkelrätt mot dess axel.

-Excentricitet, att i fallet med parabolen är det alltid värt 1.

-Grafisk representation.

Information för att bestämma alla dessa element finns i den allmänna ekvationen.

Den kanoniska formen

För att bestämma elementen i parabolen är det ibland bekvämt att överföra den allmänna formen till den kanoniska formen av samma, med hjälp av metoden för att slutföra rutor i den kvadratiska variabeln.

Denna kanoniska form är:

(X-h)² = 4p (y-k)

Där punkt (h, k) är vertex v för liknelsen. Den kanoniska formen till den allmänna ekvationen kan också bli, utveckla den anmärkningsvärda produkten och omarrangera termerna.

Exempel

Exempel 1

Följande är parabola -ekvationer i allmänhet:

a) 4x² + 5y - 3 = 0

b) 1 - 2y + 3x -och² = 0

I a) identifieras koefficienterna: a = 4, c = 0, d = 0, e = 5, f = -3. Det är en liknelse vars symmetrixel är vertikal.

Kan tjäna dig: syntetisk uppdelning

För sin del återstår den allmänna ekvationen:

- och² + 3x - 2y + 1 = 0

Och koefficienterna är: c = -1, d = 3, e = -2 och f = 1.

Exempel 2

Nästa liknelse är i en kanonisk form:

(Y-1)² = 6 (x-3)

För att hitta sin allmänna ekvation utvecklas den anmärkningsvärda produkten och parentesen utförs till höger:

och² -2y + 1 = 6x -18

Nu passerar alla termer till vänster och de grupperas bekvämt:

och² -2y + 1- 6x +18 = 0 → och² - 6x -2y + 19 = 0

Som den kvadratiska termen är och² Det är en horisontell liknelse. Koefficienterna är:

C = 1; D = -6; E = -2, f = 19.

Löst övningar

Övning 1

Nästa liknelse ges i allmänhet:

x² -10x -12y - 11 = 0

Det uppmanas att skriva det i kanonisk form.

Lösning

Gå till den kanoniska formen uppnås genom att slutföra rutor, i detta fall i variabel x. Villkoren i X börjar inom parentes:

(x² -10x) -12y - 11 = 0

Du måste förvandla vad som är inom parentes till en perfekt fyrkantig trinomial, vilket uppnås genom att lägga till 5², som naturligtvis måste subtraheras, för annars förändras uttrycket. Det återstår så här:

(x² −10x+5²) −12y - 11−5²= 0

De tre termerna inom parentes utgör den perfekta fyrkantiga trinomialen (X-5)². Det kan kontrolleras genom att utveckla denna anmärkningsvärda produkt för att bekräfta. Nu kvarstår liknelsen:

(X-5)² -12y -36 = 0

Det följande är att faktorera termerna utanför parentesen:

(X-5)² -12 (y +3) = 0

Som äntligen förvandlas till:

(X-5)² = 12 (y +3)

Exempel 2

Hitta elementen i den tidigare liknelsen och bygg din grafik.

Lösning

Vertex

Parabolens toppunkt har koordinater V (5, -3)

Det kan tjäna dig: hepagonalt prisma

Axel

Linjen x = 5.

Parameter

När det gäller parametervärdet p som visas i kanonisk form: (X-H)² = 4p (y-k) jämför båda ekvationerna:

4p = 12

P = 12/4 = 3

Orientering

Denna liknelse är vertikal och öppnar upp. Eftersom toppunktet är beläget vid x = 5, y = -3, är symmetriens axel den vertikala linjen x = 5.

Fokus

Fokus ligger på linjen x = 5, därför har den en koordinat x = 5 också.

Koordinaten och av fokus måste vara P-enheter ovanför K, det vill säga: P + K = 3 + (-3) = 0, då är fokuset vid punkt (5.0).

Rak riktlinje

Det är vinkelrätt mot axeln, därför är den av formen y = c, nu, som ett avstånd P från toppunktet är långt ifrån, men utanför liknelsen betyder det att det är på ett avstånd P under k:

y = k -p = -3-3 = -6

Rak sida

Detta segment skär till liknelsen, passerar genom fokus och är parallell med riktlinjen, därför finns det i linjen y = 0.

Grafisk representation

Det kan enkelt erhållas från gratis grafikprogramvara online, till exempel Geogebra. I ingångslådan placeras den enligt följande:

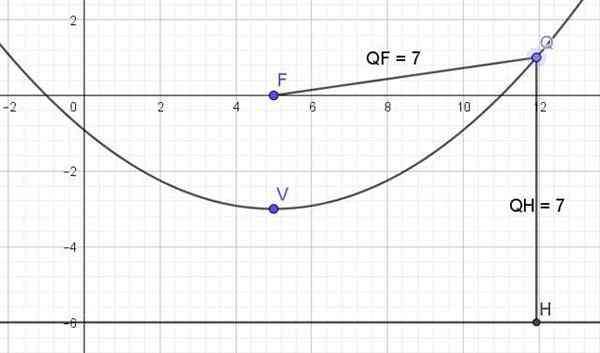Figur 3. Graf över liknelsen x² -10x -12y - 11 = 0. Källa: f. Zapata.

Referenser

1. Baldor. 1977. Elementär algebra. Venezuelanska kulturella utgåvor.
2. Hoffman, J. Urval av matematikfrågor. Volym 2.
3. Jiménez, r. 2008. Algebra. Prentice hall.
4. Stewart, J. 2006. Preccculment: Matematik för beräkning. Femte. Utgåva. Cengage Learning.
5. Zill, D. 1984. Algebra och trigonometri. McGraw Hill.