Andra graders ekvationer formel, hur man löser dem, exempel, övningar
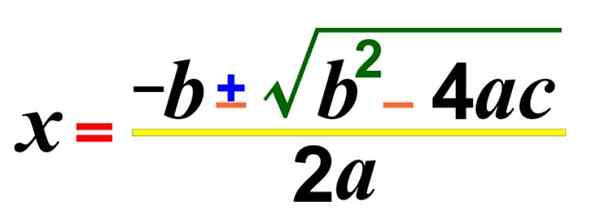
- 2469
- 559
- Per Karlsson
De Andra graden eller kvadratiska ekvationer Och en okänd har formen yxa2 + bx + c = 0. Där a ≠ 0, sedan den var 0, skulle ekvationen omvandlas till en linjär ekvation, och koefficienter a, b och c är verkliga siffror.
Det okända som ska bestämmas är värdet på x. Till exempel 3x -ekvationen2 - 5x + 2 = 0 är en komplett andra gradsekvation.
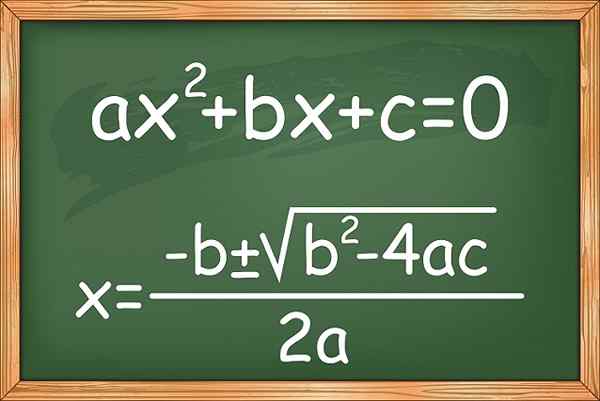 Figur 1. Formeln för att lösa andra graden eller kvadratiska ekvationer av en okänd
Figur 1. Formeln för att lösa andra graden eller kvadratiska ekvationer av en okänd Det finns också varianter som är kända som ofullständiga andra grader ekvationer, som saknar någon av termerna, förutom det yxa2. Här är några exempel:
x2 - 25 = 0
3x2 - 5x = 0
Al Juarismi, den berömda arabiska matematikern av antiken, som beskrivs i sina verk olika typer av första och andra gradsekvationer, men endast med positiva koefficienter. Men det var den franska matematiska Resolut:
Detta är en allmän formel som gör det möjligt att lösa en kvadratisk ekvation, hitta rötter eller nollor av samma, även om lösningarna inte är riktiga. Det finns också andra sätt att lösa dem.
[TOC]
Hur man löser ekvationer i andra klass?
Andra gradersekvationer kan lösas med formeln ovan, och det finns också andra algebraiska procedurer som kan fungera i vissa ekvationer.
Vi kommer att lösa den föreslagna ekvationen i början med formeln, en giltig metod för varje andra gradsekvation med en okänd:
3x2 - 5x + 2 = 0
För att använda formeln noterar vi korrekt att:
- till Det är termen med x -koefficienten med x2
- b Det är koefficienten för den linjära termen
- c är den oberoende termen.
Låt oss identifiera dem från samma ekvation:
A = 3
B = -5
C = 2
Observera att tecknet som åtföljer koefficienten måste beaktas. Nu ersätter vi dessa värden i formeln:
I telleren är symbolen för "mer - mindre" ±, vilket indikerar att mängden med rot kan tas som positiv och också som negativ. En andra gradsekvation har högst två riktiga lösningar, och denna symbol tar hänsyn till den.
Låt oss ringa x1 och x2 Till dessa två lösningar, då:
x1 = (5+1) / 6 = 1
x2 = (5-1)/6 = 4/6 = 2/3
Upplösning genom faktorisering
Några andra gradsekvationer består av trinomialer som är lätt faktor. Om så är fallet är den här metoden mycket snabbare. Tänk på ekvationen:
x2 + 7x - 18 = 0
Faktorisering har denna form:
Kan tjäna dig: kongruens: kongruenta siffror, kriterier, exempel, övningar(x +) ⋅ (x -)
De tomma utrymmena är fyllda med två siffror som, när de multipliceras 18, och när de subtraheras är 7 7 7. Tecknen inom parentes väljs med detta kriterium:
-I den första parentesen placeras tecknet mellan den första och den andra terminen.
-Och i den andra parentesen går produkten av de tecken som ses.
När det gäller siffrorna är de lätt i det här fallet: de är 9 och 2. Den äldsta är alltid placerat i den första av parentesen, så här:
x2 + 7x - 18 = (x + 9). (x - 2)
Läsaren kan kontrollera genom distribution av egendom, som när man utvecklar produkten från den högra sidan av jämlikhet erhålls vänsterns trinomial. Nu skrivs ekvationen:
(x + 9) ⋅ (x - 2) = 0
För att jämlikhet ska uppfyllas räcker det för att en av de två faktorerna är noll. Så i den första måste det göras1 = -9 eller det kan vara så att den andra faktorn avbryts, i så fall x2 = 2. Det här är ekvationslösningarna.
Grafisk metod
Rötterna eller lösningarna i den andra gradsekvationen motsvarar skärningspunkten i liknelsen y = = yxa2 + bx + c Med den horisontella axeln eller x -axeln. Så att genom att grafera motsvarande liknelse hittar vi lösningen på den andra gradsekvationen som gör y = 0.
Nedskärningarna av liknelserna med den horisontella axeln representerar ekvationens lösningar yxa2 + bx + c = 0. En liknelse som bara skär den horisontella axeln vid en enda punkt har en enda rot och detta kommer alltid att vara toppen av parabolen.
Och slutligen, om en liknelse inte skärs till den horisontella axeln, motsvarande ekvation yxa2 + bx + c = 0 Det saknar verkliga lösningar.
Att bygga en handgraf kan vara mödosamt, men med användning av program som graf online är det väldigt enkelt.
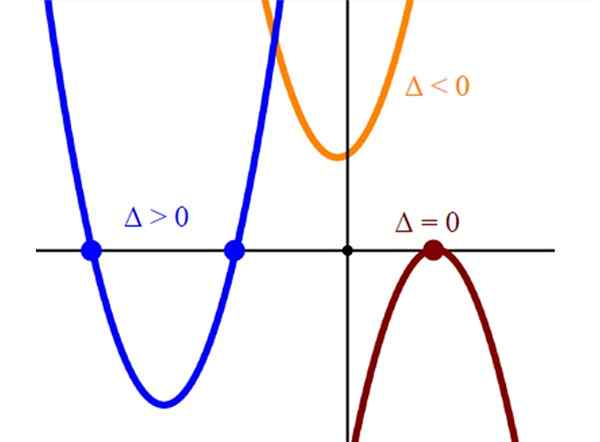 figur 2. Grafisk representation av tre typer av liknelser, med två, en och ingen korsning med den horisontella axeln. Källa: Wikimedia Commons.
figur 2. Grafisk representation av tre typer av liknelser, med två, en och ingen korsning med den horisontella axeln. Källa: Wikimedia Commons. Upplösning med vetenskaplig kalkylator
Många modeller av vetenskapliga kalkylatorer har möjlighet att lösa andra gradsekvationer (och även andra typer av ekvationer). För att veta det måste du granska menyn.
När det kvadratiska ekvationsalternativet för en okänd har valts, begär menyn att ange värdena på koefficienterna A, B och C och returnera de verkliga lösningarna om de finns. Och det finns också modeller av vetenskapliga kalkylatorer som arbetar med komplexa nummer och erbjuder dessa lösningar.
Kan tjäna dig: multiplar av 2: vad är och förklaringDiskriminerande från en andra gradsekvation
För att veta om ekvationen har verkliga lösningar eller inte, och hur många är, utan att behöva lösa först, definieras diskriminanten som mängden under kvadratroten:
Δ = b2 - 4ac
Enligt det diskriminerande tecknet är det känt hur många lösningar ekvationen har enligt detta kriterium:
-Två riktiga lösningar: Δ> 0
-En verklig lösning (eller två identiska lösningar): Δ = 0
-Ingen verklig lösning: Δ < 0
Hur många lösningar har till exempel den andra gradsekvationen -7x2 +12x + 64 = 0? Vi identifierar koefficienterna:
A = -7
B = 12
C = 64
Δ = b2 - 4ac = 122 - 4x (-7) x 64 = 144 + 1792 = 1936> 0
Ekvationen har två lösningar. Låt oss nu se den här:
x2 - 6x + 9 = 0
A = 1
B = -6
C = 9
Δ = (-6)2 - 4 x 1 x 9 = 36 - 36 = 0
Detta är en ekvation med en unik lösning eller två lika lösningar.
Exempel på enkla andra graders ekvationer
I början sa vi att andra gradsekvationerna kunde vara fullständiga om trinomialen är, och ofullständig om den linjära termen eller den oberoende termen saknades. Låt oss nu se några speciella typer:
X Formekvation2 + mx + n = 0
I detta fall är A = 1 och formeln reduceras till:
För denna typ av ekvation, och alltid beroende på de återstående koefficienterna, kan faktoriseringsmetoden fungera bra, som vi såg i föregående avsnitt.
Ofullständig ekvation av axelformen2 + C = 0
Lösningen, om den finns, är formen:
Det finns verklig lösning när en o c har ett negativt tecken, men om de två termerna har samma tecken kommer lösningen att vara imaginär.
Ofullständig ekvation av axelformen2 + Bx = 0
Denna ekvation löses snabbt genom att använda faktorisering, eftersom X är en vanlig faktor i båda termerna. En av lösningarna är alltid x = 0, den andra är så här:
yxa2 + Bx = 0
x (ax + b) = 0
AX + B = 0 → X = -B/A
Låt oss titta på ett exempel då. Lösa:
x2 - 5x = 0
x (x - 5) = 0
Därför x1 = 0 och x2 = 5
Ekvationer med nämnaren
Det finns flera rationella ekvationer, där det okända kan vara närvarande både i telleren och i nämnaren, eller till och med endast i det senare, och det genom algebraiska manipulationer reduceras till kvadratiska ekvationer.
Sättet att lösa dem är att multiplicera båda sidor av jämlikhet med den minsta vanliga multipel eller m.c.m av nämnaren och ordnar sedan villkoren. Till exempel:
Kan tjäna dig: hur många diametrar har en omkrets?Högre ordningens ekvationer som omvandlas till kvadratiska
Det finns högre ordningens ekvationer som genom en variabel förändring kan lösas som om de var kvadratiska, till exempel denna ekvation Bicadrada:
x4 - 10x2 + 9 = 0
Låt x2 = U, sedan omvandlas ekvationen till:
eller2 - 10U + 9 = 0
Denna ekvation löses snabbt genom faktorisering och hittar två siffror som multiplicerades i 9 och lade till 10. Dessa siffror är 9 och 1:
(U - 9).(U - 1) = 0
Därför är lösningarna på denna ekvation u1 = 9 och u2 = 1. Nu returnerar vi förändringen:
x2 = 9 → x1 = 3 och x2 = -3
x2 = 1 → x1 = 1 och x2 = -1
Den ursprungliga ekvationen är av ordning 4, därför har den minst 4 rötter. Exemplet är -3, -1, 1 och 3.
Enkla lösta övningar
- Övning 1
Lös följande kvadratiska ekvation med det okända i nämnaren:
Den minsta gemensamma multipeln är x (x+2) och måste multiplicera till alla termer:
Det motsvarande uttrycket kvarstår:
5x (x+2) - x = x (x+2)
Vi utvecklar:
5x2 + 10x - x = x2 + 2x
Alla termer transponeras till vänster om jämlikhet och till höger är vänster 0:
5x2 + 10x - x - x2 - 2x = 0
4x2 - 7x = 0
Vi faktor, eftersom det är en ofullständig ekvation:
x (4x - 7) = 0
En av lösningarna är x = 0, den andra är:
4x = 7
x = 7/4
- Övning 2
Hitta lösningen på andra gradsekvationerna:
a) -7x2 +12x + 64 = 0
b) x2 - 6x + 9 = 0
Lösning till
Från denna ekvation känner vi Δ -determinanten, eftersom den beräknades som ett exempel tidigare, så vi kommer att dra nytta av den och uttrycka lösningsmedelsformeln enligt följande:
x1 = (-12+44)/ - 14 = - (32/14) = - (16/7)
x2 = (-12 -44) / -14 = 4
Lösning B
Den fyrkantiga trinomialen x2 - 6x + 9 är faktoriserbar, eftersom det är en perfekt fyrkantig trinomial:
x2 - 6x + 9 = (x-3)2 = 0
Lösningen på denna ekvation är x = 3.
- Övning 3
Vad är ekvationen vars lösningar är 3 och 4?
Lösning
Det faktoriserade uttrycket är:
(x - 3) ⋅ (x - 4) = 0
Tillämpa distributionsfastigheter:
x2 - 4x -3x + 12 = 0
De två centrala termerna är liknande och kan minskas, är: lämnar:
x2 - 7x + 12 = 0
Referenser
- Baldor. 1977. Elementär algebra. Venezuelanska kulturella utgåvor.
- Hoffman, J. Urval av matematikfrågor. Volym 2.
- Jiménez, r. 2008. Algebra. Prentice hall.
- Stewart, J. 2006. Preccculment: Matematik för beräkning. Femte. Utgåva. Cengage Learning.
- Zapata, f. 4 sätt att lösa en andra gradsekvation. Återhämtat sig från: FrancesPhysics.Bloggfläck.com.
- Zill, D. 1984. Algebra och trigonometri. McGraw Hill.
- « Tilläggspolymerer struktur, egenskaper, funktion, användning
- Intrinsiska motivationsegenskaper och exempel »



\pm&space;\sqrt(-5)^2-4\times&space;3\times&space;22\times&space;3=)

^2-4c2)


x-\fracx(x+2)x+2=x(x+2))
=\frac-12\pm&space;44-14)