Hålkant

Vad är en ENDECAGON?

han hålkant, även kallad undecágono, Det är en platt geometrisk figur med 11 sidor som tillhör familjen Polygons.

Dessa utses enligt mängden sidor de har och i fallet med Endecagon härstammar deras namn från de grekiska orden "Hendeka" och "Gona": elva respektive vertex, enligt det faktum att Endecagon den har 11 vertikaler eller tips.

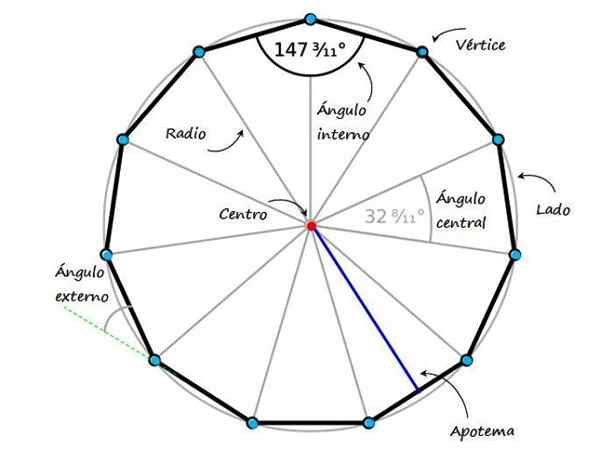
Figur 1. En vanlig endekagon och dess element. Källa: f. Modifierad wikimedia commons sko.

Regelbundna polygoner delar en serie distinkta egenskaper, särskilt. Figur 1 visar en regelbunden endecagon och dess mest betydande egenskaper:

• Sidor, Totalt 11.
• Häckar, Det finns också 11 punkter som går med i två sidor i rad (i föregående siffra är de blå punkterna och i figur 3 namnges de också med stora bokstäver).
• Centrum, likvärdig punkt för både vertikalerna och sidorna.
• Diagonaler, Linjer som går med i ett toppunkt med ett annat icke -konsekutivt toppunkt, totalt 44.
• Inre vinklar, De som bildas mellan två angränsande sidor på den inre sidan av Endecagon. Om Endecagon är regelbunden mäter alla interna vinklar 147 ^3/11 º.
• Yttre vinklar, De bildas mellan ena sidan och förlängningen av en av de på varandra följande sidorna.
• Radio, Avstånd från centrum till ett toppunkt.
• Centralvinkel, Det i fallet med regelbundna Endecagon mäter 32 ^11/11 º, vars sidor är två angränsande segment och vinkeln sammanfaller med mitten.
• Apotem, vinkelrätt segment som förenar mitten av en sida med mitten av figuren.

Det kan tjäna dig: Hipparco of Nicea: Biografi och bidrag till vetenskapen

Hur man gör en vanlig Endecagon?

För att rita en regelbunden endecagon, vars sidor mäter samma sak, behöver du regel och kompass. Ett sätt att göra layouten följer dessa steg:

1.- Rita en omkrets och två diametrar av den, en vertikal och en annan horisontell. Punkterna i omkretsen som bestäms av dessa diametrar är namngivna och B (horisontell diameter) och C och D (vertikal diameter).

2.- Öppna kompassen med måtten på cirkelradie, stödja spetsen vid punkt D på CD -diametern och dra en första båge som korsar omkretsen vid punkt E.

3.- Med samma mått stöder kompassens spets vid punkt A och rita en andra båge som korsar omkretsen vid punkt F och samtidigt passerar genom mitten av samma.

4.- Öppna takten med spetsen som stöds av E och till punkt F, och ritar en tredje båge som skär den vertikala diametern vid punkt G.

5.- Öppna nu kompassen mellan punkterna f och g. Detta kommer att vara måttet på Endecagon -sidan. Spetsen på kompassen stöds i F och drar en fjärde båge som skär till omkretsen vid punkt H, FH -sidan tillhör redan Endecagon och dras genom att gå med i punkterna med hjälp av regeln.

6.- Spetsen på kompassen vilar successivt vid punkt H och utarbetas försiktigt och förenar de punkter som bestäms av segment, tills de elva sidorna av polygonen.

Exempel på endecágonos

Det finns flera typer av ENDECARGONS, beroende på måtten på deras sidor och deras inre vinklar, under några exempel:

Regelbundna och oregelbundna endekonister

-Regelbunden, Om alla sidor och inre vinklar mäter samma.

Kan tjäna dig: euler nummer eller nummer e: hur mycket ok, egenskaper, applikationer

-Oregelbunden, När deras sidor har olika mått.

Följande figur visar en regelbunden enkagon i den interna konturen av en amerikansk dollar med figuren Susan B. Anthony (1820-1906), en aktivist av kvinnors rättigheter född i Massachusetts, USA. Endecagon har också använts som en del av utformningen av andra mynt över hela världen.

figur 2. En regelbunden endecagon som utgör en del av Dollar Susan B -designen. Anthony, myntade mellan 1979 och 1981 och lanserades senare igen 1999. Källa: Wikimedia Commons.

Konvexa och konkava ENDECARGONS

Endecargars skiljer sig åt beroende på deras inre vinklar, till exempel kan de vara:

-Konvex, Om de inre vinklarna är mindre än 180º.

-Konkav, När det finns inre vinklar större än 180º.

Endecagon som dekorerar dollarn Susan b. Anthony är konvex, eftersom måttet på någon av dess inre vinklar är mindre än 180º. Dess värde beräknas genom en formel som beror på antalet sidor på figuren (se följande avsnitt).

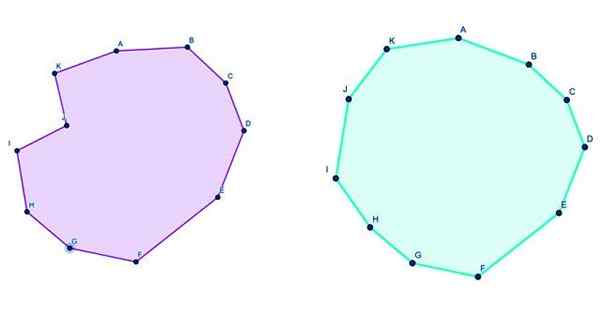Figur 3. Till vänster en konvex endekagon och till höger en konkav Endecagon. Källa: f. Zapata genom geogebra.

Formler för Endecagon

Formel för inre vinklar

För att bestämma måtten I i grader, av de inre vinklarna på någon vanlig polygon av n sidor, följande formel används:

 Ersätta antalet sidor på endecagon n = 11 i formeln erhålls:

 Och eftersom de inre vinklarna i den vanliga Endecagon är mindre än 180 ° är denna siffra en konvex polygon.

Summan av de inre vinklarna för en vanlig polygon hittas av denna formel, giltig för hela och mer än 2:

Kan tjäna dig: Vinklar i omkretsen: typer, egenskaper, lösta övningar

S = (n - 2) x 180º

Ersätta n = 11 resultat:

S = (11 - 2) x 180º = 1620º

Yttre vinklar

För att känna till måtten på inre vinklar tillämpas det att summan av en inre och en yttre vinkel är lika med 180º:

180 º - 147 ^3/11º = 32 ^11/11º.

Omkrets

Omkretsen är summan av sidorna på Endecagon, vare sig det är regelbundet eller inte. I fallet med regelbunden endecagon, om ℓ Det är längden på en sida, omkretsen multipliceras med n, Mängden sidor.

Därför är omkretsen P för den vanliga Endecagon:

P = 11 ℓ

Område

Genom att känna till sidan kan området beräknas med formeln:

Vilket är ungefär:

A = 9.3656 ∙ ℓ²

Ett annat sätt att hitta området, förutsatt att Endecagon är regelbundet, är att dela upp det i bastrianglar som är lika med sidan ℓ och höjden lika med längden på apotem l l_TILL.

Området för varje triangel beräknas av:

Area = bas x höjd /2

Det beroende på apotem är också skriven som:

Area = ℓ. L_TILL /2

Och den totala arean för Endecagon multiplicerar triangelområdet med 11:

A = 11ℓ. L_TILL /2

När det gäller omkretsen är det vanliga Endecagon -området:

A = p. L_TILL /2

Diagonaler

Antalet diagonaler beräknas genom att göra n = 11 i följande formel:

 D = [11 x (11-3)]/2 = 44 diagonaler.

Träning löst

Beräkna omkrets och område för en regelbunden endekagon på 20 cm sida.

Lösning

Omkretsen är:

P = 11 ℓ =11 × 20 cm = 220 cm.

Och dess område är:

A = 9.3656 ∙ ℓ²= 9.3656 × (20 cm)²= 3746.2 cm²

Referenser

1. Alexander, D. 2013. Geometri. Femte. Utgåva. Cengage Learning.
2. Tecknare. Endecágono inskriven i en omkrets (11 sidor polygon). Återhämtat sig från: YouTube.com.
3. Problem och ekvationer. Område och omkretsberäknare av den vanliga Endecagon. Hämtad från: Problem Syuses.com.
4. Sangaku matematik. Element i en polygon och dess klassificering. Återhämtat sig från: Sangakoo.com.
5. Automatisk problemlösning av geometri. Endecagon. Återhämtat sig från: scuolaetrica.Artikel.
6. Wolfram Mathworld. Hålkant. Återhämtat sig från: Mathworld.Volfram.com.