Absolutvärde

Vad är det absoluta värdet?

han absolutvärde av ett verkligt nummer definieras som avståndet mellan det numret och 0 i den verkliga linjen. För att vara ett avstånd är dess värde alltid positivt eller noll och lika med siffran i antalet.

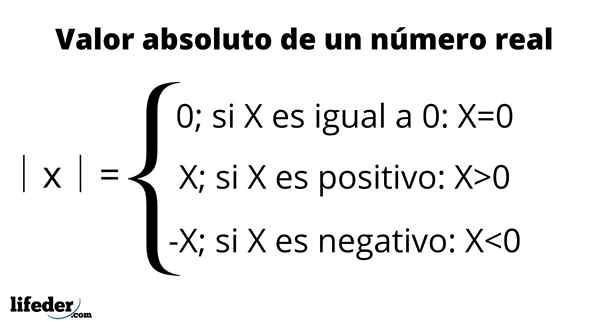
Det absoluta värdet representeras genom att placera numret mellan två vertikala staplar, en symbol som läses: "absolut värde på”, Som sammanfattas i följande tabell:

Till exempel skrivs det absoluta värdet på -3 som │ -3│ och är lika med 3. Detta innebär att mellan -3 och 0 finns det tre enheter, som representerar siffrorna på den verkliga linjen. Å andra sidan är det absoluta värdet på +3 eller helt enkelt 3, också lika med 3, eftersom det är tre enheter genom att mäta dess avstånd till 0.

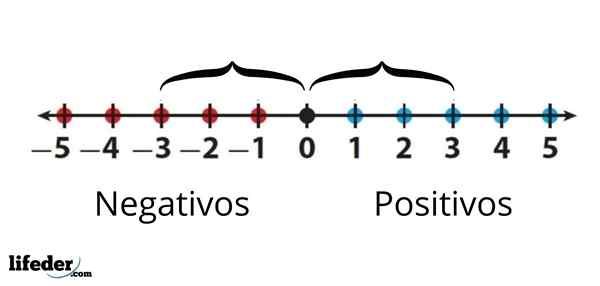Det absoluta värdet på -3 är lika med det absoluta värdet på +3, eftersom avståndet mellan antingen till 0 är detsamma är detsamma

Sammanfattningsvis är det absoluta värdet på ett antal samma siffra för antalet men alltid med ett positivt tecken.

Egenskaper med absolut värde

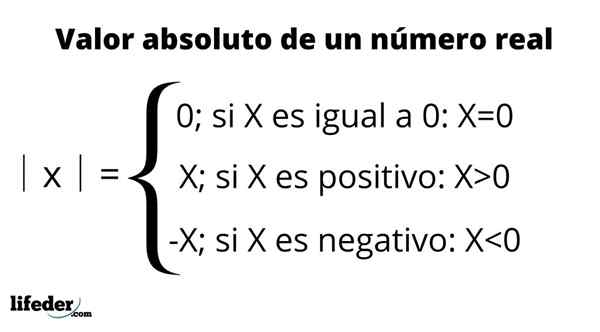Definition av absolut värde

Huvudegenskaperna för absolut värde:

• 1) Det absoluta värdet på ett antal är alltid positivt eller 0, därför:

│x│≥ 0

• 2) Det absoluta värdet på noll är också noll, det vill säga │0│ = 0, därför kan det bekräftas att:

│x│ = 0, ja y bara om x = 0

• 3) För varje nummer X som tillhör uppsättningen av verkliga siffror är det absoluta värdet på x lika med det absoluta värdet på - x:

│x│ = │ - x│

• 4) Om det absoluta värdet på ett x -nummer är a, betyder det att det finns två alternativ för det numret: i) x = +a eller ii) x = -a.

Det kan tjäna dig: Mary Travels 2/4 av CyclePist, Melissa Travels 4/8 och Anahi Travels 3/6

Till exempel, om det absoluta värdet på ett nummer är 5 är de två möjligheterna att antalet är +5 eller -5.

Operationer med absolut värde

Följande egenskaper är mycket användbara för att göra operationer med absoluta värden:

• 5) För "X" och "Y" som är två verkliga siffror är följande ojämlikhet alltid uppfyllda, kallas triangulär ojämlikhet av absolut värde:

│x│+│y│≥ │x+y│

Till exempel vara:

x = -6

y = 9

Den vänstra sidan av ojämlikhet är:

│-6│ + │9│ = 6 + 9 = 16

Och höger sida är:

│-6+9│ = │3│ = 3

Uppenbarligen är 16 större än eller lika med 3, och detta är alltid fallet när siffrorna x och har olika tecken. Om de har lika tecken erhålls jämlikhet. Se detta andra exempel med två andra olika värden:

x = -5

y = -3

│-5│+│-3│≥ │-5-3│

5+3≥│-8│

Verkligen:

8 = 8

• 6) Produkten av respektive absoluta värden på två verkliga nummer "X" och "Y" är lika med det absoluta värdet på produkten av siffrorna:

│x│ ∙ │y│ = │x ∙ y│

Återigen är värdena:

x = -6

y = 9

Så:

│-6│ ∙ │9│ = 6 ∙ 9 = 54

Vilket är lika med:

│ (-6) ∙ 9│ = │-54│ = 54

• 7) Kvoten på det absoluta värdet på två verkliga siffror "X" och "Y", med den olika nämnaren av 0, är ​​det absoluta värdet på kvoten mellan dessa siffror:

Så länge och ≠ 0.

Exempel:

Exempel på absolut värde

Enkla exempel

Att beräkna det absoluta värdet för alla verkliga nummer är mycket enkelt, till exempel är det absoluta värdet för följande siffror:

a) │-14│ = 14

b) │-(-5) │ = │5│ = 5

c) │π│ = π

Beräkningar med det absoluta värdet på ett verkligt antal

Utför följande operationer som involverar det absoluta värdet:

A) 2⋅│8│ + 5⋅│ -16│ -⋅│4│ = (2⋅8) + (5⋅16) - 4 = 16 + 80 - 4 = 92

b) │5- (8⋅3) │- 6 + │81 ÷ (-3) │ 

Kan tjäna dig: hälften av 15

Detta är en kombinerad operation, så det är att föredra att lösa den med steg. Det första absoluta värdet är:

│5- (8⋅3) │ = │5-24│ = │-19│ = 19

Det andra absoluta värdet som visas beräknas enligt följande:

│81 ÷ (-3) │ = │-27│ = 27

Sedan samlas de erhållna resultaten och den slutliga beräkningen genomförs:

│5- (8⋅3) │- 6 + │81 ÷ (-3) │ = 19- 6 + 27 = 40

Avståndet mellan två punkter på den verkliga linjen

Det absoluta värdet visas i många applikationer, till exempel att hitta avståndet mellan två siffror som tillhör den verkliga linjen. Om A är ett riktigt nummer finns det på den verkliga linjen vid den punkt vars abscissa är "A", detsamma händer med ett riktigt nummer B.

Låt "A" och "B" två siffror på den verkliga linjen, avståndet som skiljer dem är:

d_Ab = │b - a│

Som också kan beräknas av:

d_Ab = │A - B│

Till exempel är avståndet mellan A = 5 och B = 12:

D = │5−12│ = │12−5│ = 7

På detta sätt är det absoluta värdet på subtraktionen mellan två verkliga siffror helt enkelt avståndet som skiljer dem på den verkliga linjen.

Absolut värdefunktion

Den absoluta värdet är en applikation som går på uppsättningen av verkliga siffror ℛ fram till ℛ⁺, vilket motsvarar varje verkligt nummer dess absoluta värde. Det definieras av:

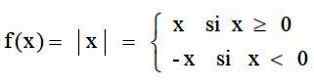
Och dess graf har den typiska V -formen:

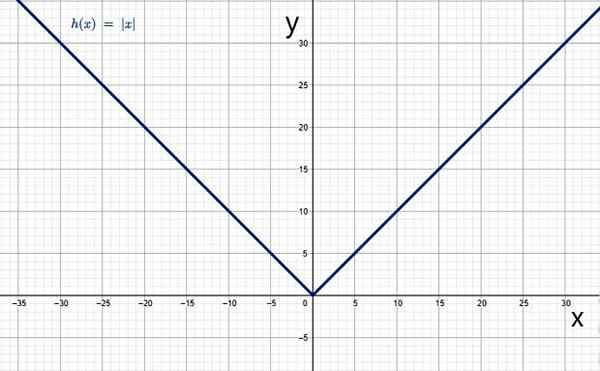Det absoluta värdet som en funktion. Källa: f. Zapata genom geogebra.

Egenskaper för den absoluta värdefunktionen

-Din domän är uppsättningen av alla riktiga siffror.

-Det är kontinuerligt.

-Det är till och med, eftersom det uppfylls att f (x) = f (-x), därför är den vertikala axeln en symmetrixaxel.

-Räckvidden för den absoluta värdet är uppsättningen av positiva riktiga inklusive 0, eftersom funktionen alltid representerar ett avstånd, och detta är alltid positivt eller null.

Kan tjäna dig: vad är riktlinjen? (Geometri)

-Det är en funktion efter sektioner eller efter delar.

-Minskar i intervallet (-∞, 0) och växer in (0,+∞).

Det absoluta värdet kan också vara en kvadratisk eller annan funktion, till exempel kan det definieras:

• f (x) = │x²-5x+3│
• g (x) = │sen x│

Det absoluta värdet är ansvarigt för att bli positiva bilderna av argumentet som har ett negativt tecken.

Löst övningar

Övning 1

Utvärdera följande algebraiska uttryck med absolut värde:

a) │2x -5│ + │ --x + 1│ vid x = 3

b) │ (x - 5) ÷ (x+4) │ vid x = −1

Lösning till

│2⋅3−5│ + │ - 3 + 1│ = │6−5│ + │ - 2│ = │1│ + 2 = 3

Lösning B

│ (−1−5) ÷ (−1+4) │ = │ (−6) ÷ (3) │ = │ - 2│ = 2

Övning 2

Vad är uppsättningen värden som representerar följande ojämlikhet?

│x│≤ 3

Lösning

Ojämlikhet representerar alla verkliga siffror vars absoluta värde är mindre än eller lika med 3, därför är det uppsättningen av alla siffror mellan -3 och +3, inklusive dessa.

I intervallnotationen kvarstår det:

[-3,3]

Övning 3

Lös följande ekvation med absolut värde:

│2x-1│ = 5

Lösning 

Som tidigare anges, för att lösa en ekvation med absolut värde är det nödvändigt att överväga de två alternativen. Jag menar ja:

│f (x) │ = c

Så:

1) f (x) = c

2) f (x) = -c

Därför har denna ekvation, vars argument är linjärt, två lösningar:

Första lösning

2x - 1 = 5

2x = 6 ⇒ x₁ = 3

Andra lösning

2x - 1 = -5

2x = -4 ⇒ x₂ = -2

Vid utvärdering av x₁ = 3 eller x₂ = -2 I den ursprungliga ekvationen måste en jämlikhet erhållas, på detta sätt verifieras det att de erhållna värdena är lösning av den föreslagna ekvationen. Verkligen:

│ (2⋅3) -1│ = │6-1│ = 5

Och när man försöker med det andra alternativet erhålls också en jämlikhet:

│2⋅ (-2) -1│ = │-4-1│ = 5

Referenser

1. Baldor, a. 2005. Algebra. Kulturhem.
2. Larson, r. 2012. Förkalkning. 8th. Utgåva. Cengage Learning.
3. Hoffman, J. Urval av matematikfrågor. Volym 2.
4. Stewart, J. 2007. Preccculment: Matematik för beräkning. Femte. Utgåva. Cengage Learning.
5. Zill, D. 1984. Algebra och trigonometri. McGraw Hill.