Mekaniska energiformler, koncept, typer, exempel, övningar

De mekanisk energi av ett objekt eller ett system definieras som summan av dess potentiella energi och dess kinetiska energi. Som namnet antyder förvärvar systemet mekanisk energi tack vare verkan av mekaniska krafter som vikt och elastisk kraft.

Enligt mängden mekanisk energi som kroppen har kommer den också att ha förmågan att utföra ett mekaniskt arbete.

Figur 1. Roller Mountain Car Movement kan beskrivas genom bevarande av mekanisk energi. Källa: Pixabay.

Energin - den typ som är - är en skalformig, och saknar därför riktning och mening. Vara OCH_m En objekts mekaniska energi, ELLER dess potentiella energi och K Dess kinetiska energi, formeln för att beräkna den är:

OCH_m = K + u

Enheten i det internationella energisystemet av något slag är Joule, som förkortas som J. 1 J motsvarar 1 n.m (Newton per meter).

När det gäller kinetisk energi beräknas den enligt följande:

K = ½ m.v²

Var m Det är objektets massa och v Dess hastighet. Kinetisk energi är alltid en positiv mängd, eftersom massan och kvadratet är. När det gäller potentiell energi, om det handlar om gravitationspotential energi, har du:

U = m.g.h

Här m Det är fortfarande degen, g Det är tyngdkraftens acceleration h Det är höjden med avseende på referensnivån eller om det föredras, marken.

Nu, om kroppen i fråga har elastisk potentiell energi -kan det vara en vår -det beror på att den är komprimerad eller kanske långsträckt. I så fall är den tillhörande potentiella energin:

U = ½ kx²

Med k som vårkonstanten, vilket indikerar hur lätt eller svårt det är att deformera det och x Längden på nämnda deformation.

[TOC]

Begrepp och egenskaper hos mekanisk energi

Fördjupning av definitionen som givits tidigare beror mekanisk energi sedan på energin förknippad med kroppsrörelse: kinetisk energi, plus bidraget från potentiell energi, som som vi sa kan vara gravitation, på grund av både vikt och vikt och position som upptar kroppen med respekt för jorden eller referensnivån.

Låt oss illustrera detta med ett enkelt exempel: Anta att du har en kruka på golvet och i vila. Eftersom det fortfarande är, har den ingen kinetisk energi, och den är också på marken, en plats där den inte kan falla; Därför saknar den gravitationspotential energi och dess mekaniska energi är 0.

Anta nu att någon placerar potten precis vid kanten av ett tak eller ett fönster, vid 3.0 meter högt. För detta var personen tvungen att göra ett jobb mot allvar. Potten har nu gravitationspotential energi, den kan falla från den höjden och dess mekaniska energi är inte längre ogiltig.

figur 2. En kruka ovanpå ett fönster har gravitationspotential energi. Källa: Pixabay.

Under dessa omständigheter har potten OCH_m = U Och denna mängd beror på pottenhöjden och vikten, som anges tidigare.

Låt oss säga att potten faller eftersom den var i en osäker position. När hastigheten ökar och med den är dess kinetiska energi, medan gravitationspotentialen energi minskar, eftersom den tappar höjden. Den mekaniska energin när som helst av hösten är:

Kan tjäna dig: vad är de härledda storleken?

OCH_m = U + k = ½ m.v² + m.g.h  

Konservativa och icke-konservativa krafter

När potten är i en viss höjd har den gravitationspotential energi eftersom vem klättrade på den, gjorde ett jobb mot tyngdkraften. Storleken på detta arbete är värt densamma som den som gör tyngdkraften när potten faller av Från samma höjd, men det har motsatt tecken, eftersom det gjordes mot det.

Det arbete som krafter som tyngdkraft och elasticitet beror endast på den första positionen och den slutliga positionen som förvärvats av objektet. Oavsett banan följde för att gå från en till en annan, bara värdena i sig är viktiga. De krafter som uppför sig på detta sätt kallas Konservativa krafter.

Och eftersom de är konservativa tillåter de att det arbete som utförs av dem som kan lagras som potentiell energi i konfigurationen av objektet eller systemet. Det är därför potten på kanten av fönstret eller taket, hade möjlighet att falla och med den att utveckla rörelse.

Å andra sidan finns det krafter vars verk beror på vägen följt av objektet som de agerar. Friktionen tillhör denna typ av krafter. Skor Sules kommer att spenderas mer när du åker från en plats till en annan på en väg med många varv än när du går till ytterligare en direkt.

Friktionskrafter gör ett jobb som minskar kroppens kinetiska energi, eftersom den bromsar dem. Och det är därför den mekaniska energin i de system där friktion fungerar tenderar att minska.

En del av det arbete som gjorts med kraft förloras av värme eller ljud, till exempel.

Typer av mekanisk energi

Mekanisk energi är, som sagt, summan av kinetisk energi och potentiell energi. Nu kan potentiell energi komma från olika konservativa krafter: vikt, elastisk styrka och elektrostatisk kraft.

- Rörelseenergi

Kinetisk energi är en skalmängd som alltid blir rörelsen. Varje partikel eller rörande föremål har kinetisk energi. Ett objekt som rör sig i en rak linje har kinetisk energi av översättning. Detsamma händer om det roterar, i det här fallet talas det om roterande kinetisk energi.

Till exempel har en bil som rör sig längs en väg kinetisk energi. Också en fotbollsboll när du rör sig längs banan eller personen som går snabbt för att nå kontoret.

- Potentiell energi

Det är alltid möjligt att associera en skalfunktion som kallas potentiell energi till en konservativ kraft. Följande skiljer sig:

Potentiell gravitationsenergi

Den som alla föremål har i kraft av sin höjd med avseende på marken eller referensnivån som har valts som sådan. Som ett exempel har någon som är i vila på terrassen i en byggnad på 10 våningar potentiell energi 0 med avseende på terrassens mark, men inte med avseende på gatan som ligger 10 våningar nedanför.

Elastisk potentiell energi

Det lagras vanligtvis i föremål som ligor och fjädrar, associerade med deformation de upplever när de sträcker eller komprimerar dem.

Elektrostatisk potentiell energi

Det lagras i ett system med elbelastningar i jämvikt på grund av den elektrostatiska interaktionen mellan dem. Anta att det finns två elektriska laddningar av samma separata skylt på ett litet avstånd; Eftersom elektriska laddningar av samma skylt avvisas, förväntas det att en extern agent har gjort arbete för att föra dem närmare.

Kan tjäna dig: växlande aktuella kretsar: typer, applikationer, exempel

När det är placerat lyckas systemet lagra det arbete som agenten gjorde för att konfigurera dem, i form av elektrostatisk potentiell energi.

Bevarande av mekanisk energi

Återvända till den fallande potten förvandlas den gravitationella potentiella energin som den hade när den var på taket till kinetisk rörelse av rörelse. Detta ökar på bekostnad av den första, men summan av båda förblir konstant, eftersom potten är aktiverad av tyngdkraften, vilket är en konservativ kraft.

Det finns ett utbyte mellan en typ av energi och en annan, men det ursprungliga beloppet är detsamma. Därför är det giltigt att bekräfta att:

Initial mekanisk energi = slutlig mekanisk energi

OCH_{Initial m} = E_{M final}

Alternativt:

K_första + ELLER_första = K _slutlig + ELLER_slutlig

Med andra ord förändras inte mekanisk energi och ∆E_m = 0. "∆" -symbolen betyder variation eller skillnad mellan ett slutligt belopp och en initial.

För att korrekt tillämpa principen om bevarande av mekanisk energi på problemlösning är det nödvändigt att:

-Det gäller endast när krafterna som verkar på systemet är konservativa (svårighetsgrad, elastisk och elektrostatisk). Isåfall: ∆E_m = 0.

-Studiesystemet måste isoleras. Det finns ingen energiöverföring på något sätt.

-Om i ett problem Fiving dyker upp, då ∆E_m ≠ 0. Trots detta kan problemet lösas genom att hitta det arbete som utförts av konservativa krafter, eftersom det är orsaken till minskningen av mekanisk energi.

Avdrag för mekanisk energibesparing

Anta att en konservativ kraft verkar på systemet som gör ett jobb W. Detta arbete orsakar en förändring i kinetisk energi:

W = ∆k (Cinetic Work-Energy Theorem)

Det är viktigt att notera att arbets-energi-teoremkinetiken är tillämplig även i fallet med icke-konservativa krafter.

Å andra sidan är arbetet också ansvarigt för förändringen i potentiell energi, och vid en konservativ kraft definieras förändringen i potentiell energi som det negativa av det arbetet:

W = -∆u

Matcha dessa ekvationer, eftersom båda hänvisar till det arbete som gjorts på objektet:

∆k = -∆u 

K_F - K_antingen = -(u_F - ELLER_antingen)

Abonnemang symboliserar "final" och "initial". Gruppering:

K_F + ELLER_F = K_antingen + ELLER_antingen                                                    

Exempel på mekanisk energi

Många objekt har komplexa rörelser, där det är komplicerat att hitta uttryck för position, hastighet och acceleration som en funktion av tiden. I sådana fall är tillämpning av den mekaniska energibesparingsprincipen ett mer effektivt förfarande än att försöka tillämpa Newtons lagar direkt.

Låt oss titta på några exempel där mekanisk energi bevaras:

-En skidåkare som glider nedförsbacke över snöiga kullar, under förutsättning att frånvaron av friktion antas. I detta fall är vikten orsakande kraften i rörelsen i hela banan.

-Ryska bergsvagnar, Det är ett av de mest typiska exemplen. Här är också vikten den kraft som definierar rörelse och mekanisk energi bevaras om det inte finns någon friktion.

Kan tjäna dig: joniseringsenergi

-Den enkla pendeln Den består av en massa som är föremål för ett oextlöst rep -det förändrar inte längden -som kort skiljer sig från den vertikala och får svänga oscillera. Vi vet att det så småningom kommer att stoppa på grund av friktion, men när friktionen inte beaktas bevaras mekanisk energi också.

-Ett block som påverkar en vår Fixat i ena änden på väggen, alla läggs på ett mycket smidigt bord. Blocket komprimerar våren, reser ett visst avstånd och skjuts sedan i motsatt riktning, eftersom våren sträcker sig. Här förvärvar blocket sin potentiella energi tack vare det arbete som gör våren på det.

-Vår och boll: När en fjäder komprimeras av en boll, denna studsande. Detta beror på att när våren släpps blir potentiell energi kinetisk energi i bollen.

-Trampolinhopp: Det fungerar liknar en vår, elastiskt främjar den person som hoppar på honom. Detta använder sig av sin vikt när man hoppar, med vilken den deformeras trampolinen, men den här, när den återgår till sin ursprungliga position, ger impulsen till jumperen.

Figur 3. Springboard fungerar som en vår och främjar de människor som hoppar på den. Källa: Pixabay.

Löst övningar

- Övning 1

Ett föremål av massa M = 1 kg tappas av en ramp från en höjd av 1 m. Om rampen är extremt smidig, beräkna kroppshastigheten precis när våren kolliderar.

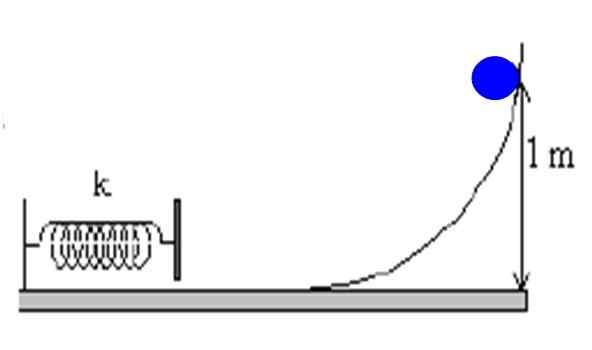Figur 4. Ett föremål sjunker på en ramp utan friktion och komprimerar en fjäder som är fäst vid väggen. Källa: f. Zapata.

Lösning

Uttalandet rapporterar att rampen är smidig, vilket innebär att den enda kraften som verkar på kroppen är dess vikt, en konservativ kraft. Således indikeras det att tillämpa bevarande av mekanisk energi mellan alla punkter i banan.

Tänk på punkterna i figur 5: A, B och C.

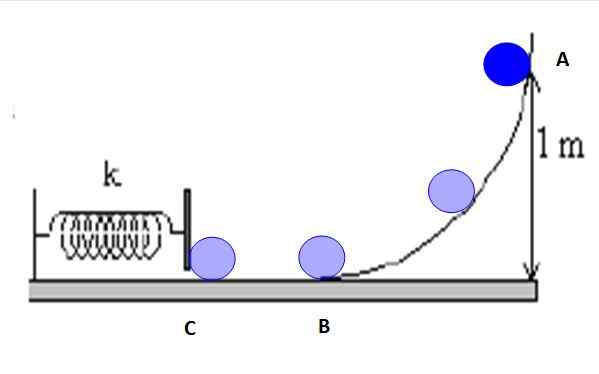Figur 5. Vägen som följer objektet är friktion och mekanisk energi bevaras mellan alla punkter. Källa: f. Zapata.

Det är möjligt att fastställa bevarande av energi mellan A och B, B och C eller A och C, eller någon av de mellanliggande punkterna på rampen. Till exempel mellan A och C har du:

Mekanisk energi vid a = mekanisk energi i c

OCH_ma = E_Mc

K_TILL + ELLER_TILL = K_C + ELLER_C

½ m.v_TILL² + m.g.h_TILL = ½ m v_C² + m.g.h_C

Som släpps från punkt A, hastigheten V_TILL = 0, å andra sidan h_C = 0. Dessutom avbryts massan, eftersom den är en vanlig faktor. Så:

g.h_TILL = ½ v_C²

v_C²= 2 g.h_TILL

- Övning 2

Hitta den maximala komprimeringen som fjädern i övningen löst 1 kommer att uppleva, om den elastiska konstanten av samma är 200 n/m.

Lösning

Fjäderns elastiska konstant indikerar att kraften som ska appliceras för att deformera en längdenhet. Eftersom vårens konstant är värd k = 200 n/m, indikerar detta att 200 n krävs för att komprimera eller sträcka den 1 m.

Vara x Avståndet som objektet komprimerar våren innan du stannar vid punkt D:

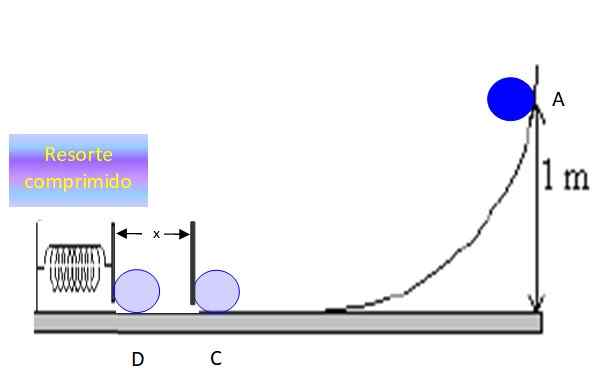Figur 6. Objektet komprimerar våren ett x -avstånd och stannar en stund. Källa: f. Zapata.

Bevarande av energi mellan punkterna C och D, konstaterar att:

K_C + ELLER_C = K_D + ELLER_D

Vid punkt C har den inte gravitationspotential energi, eftersom dess höjd är 0, men den har kinetisk energi. I d har han slutat helt, därför där k_D = 0, men istället har du till förfogande den potentiella energin från den komprimerade våren u_D.

Bevarande av mekanisk energi kvarstår:

K_C = U_D

½ mV_C² = ½ kx²

 

Referenser

1. Bauer, w. 2011. Fysik för teknik och vetenskap. Volym 1. MC Graw Hill.
2. Figueroa, D. 2005. Serie: Physics for Science and Engineering. Volym 1. Kinematik. Redigerad av Douglas Figueroa (USB).
3. Riddare, r.  2017. Fysik för forskare och teknik: En strategistrategi. Pearson.
4. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14th. Ed. Volym 1.
5. Wikipedia. Mekanisk energi.Återhämtad från: är.Wikipedia.org.