Rotationsbalansformler och ekvationer, exempel, övningar

Det hävdas att en utökad kropp är i rotationsbalans När summan av momenten som verkar på den är noll. Detta betyder inte att objektet nödvändigtvis är i vila, utan snarare att det inte finns någon nettotrend att ändra dess rörelseläge till en annan.

Ett objekt som rör sig med konstant hastighet gör det längs en rak linje och vi kan betrakta det i rotationsbalans. Nu kretsar föremål eftersom det finns krafter som verkar på dem på ett sådant sätt att det är en rotation. Förmågan hos en kraft att producera rotation, kallad vridmoment eller Torca, Det beror inte bara på styrkans intensitet, utan också där den appliceras.

Figur 1. Figurens upphängningsbrygg var utformad för att vara i rotationsbalans. Källa: Wikimedia Commons.

Vi känner igen detta omedelbart när en stängd dörr kommer att öppna: styrkan appliceras aldrig nära gångjärnen, men långt ifrån dem, så handtaget placeras så långt som möjligt, bredvid dörren till dörren.

Gångjärnen passerar dörrens rotationsaxel. Insisterar på att trycka det mycket nära gångjärnen måste du göra en stor ansträngning för att dörren till och med ska röra sig lite.

I litteraturen är vridmomentet med olika namn: Moment of Torsion, Torsion, Moment of a Force and Torca. Alla är synonymer.

Så vi måste känna till momenten som verkar på ett objekt för att fastställa rotationsbalansens tillstånd.

[TOC]

Rotationsbalansförhållanden

Rotationsbalansens tillstånd är:

Summan av alla stunder eller vridmoment som verkar på en kropp, beräknad med avseende på alla axlar, måste vara ogiltiga.

Objektet i fråga måste utvidgas, eftersom partiklar per definition bara har översättningsbalans.

Du kan tjäna dig: Newtons andra lag: applikationer, experiment och övningar

Det kan finnas tillämpade krafter på kroppen och det finns fortfarande en rotationsbalans, medan krafterna inte vänder den.

Det kan också finnas rörelse, till och med accelererad, men alltid längs en rak linje, eftersom inte alla krafter orsakar utseendet på vridmoment. Dessa visas när krafterna inte agerar hela tiden samma handlingslinje.

Vridmoment eller kraft av kraft

Vridmomentet betecknas med de grekiska texterna τ, i fetstil Eftersom det är en vektor och vi skiljer den från dess storlek eller modul, vilket är en skalar. Det beror på den applicerade kraften F, av vektorn r som är riktad från rotationsaxeln eller till appliceringspunkten och slutligen av vinkeln mellan dessa två vektorer.

Det korrekta förhållandet mellan dessa storlekar upprättas genom vektorprodukten:

τ = r x F

Och vridmomentmodulen, betecknad utan djärv är:

τ = r⋅f⋅sen θ

Där θ är vinkeln mellan r och F. Vridmomentenheter är helt enkelt N⋅m i det internationella systemet.

I figuren finns en engelsk nyckel som den är avsedd. För detta prövas två krafter F_TILL och F_B.

F_TILL är närmare O och har en vektor r_TILL eller kortare spakarm, producerar därför inte så mycket vridmoment och kraft F_B, Som har samma storlek, men det har en vektor r_B större.

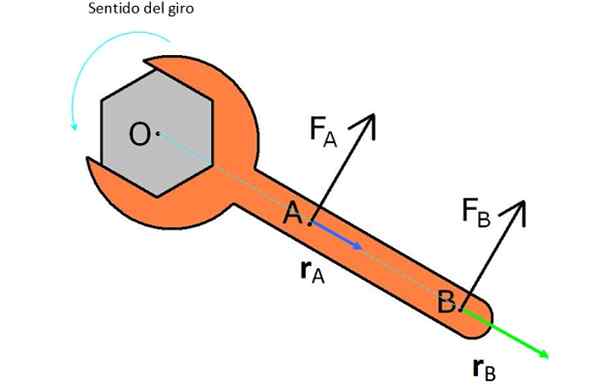figur 2. Krafter och armar tillämpas på en engelsk nyckel för att vända den i strid med klocknålarna. Källa: Wikimedia Commons.

Observera att om du vill rotera muttern i ett schema måste du tillämpa krafterna i motsatt riktning på hur de visas i figuren.

Riktning och känsla av vridmoment

Eftersom vridmomentet är resultatet av tvärprodukten mellan styrka och positionsvektorer, och dessa är i den engelska nyckelns plan, måste vridmomentet vara en vektor vinkelrätt mot det planet, det vill säga riktat mot läsaren eller inuti sidan.

Kan tjäna dig: atmosfärstryck: normalt värde, hur det mäts, exempel

Enligt konventionen är vridmomentet positivt om det ger vänd i motsatt riktning på klocknålarna och negativt om det gör det i klockans riktning.

Riktningen och riktningen för det resulterande vridmomentet bestäms lätt av regeln för höger hand som visas nedan:

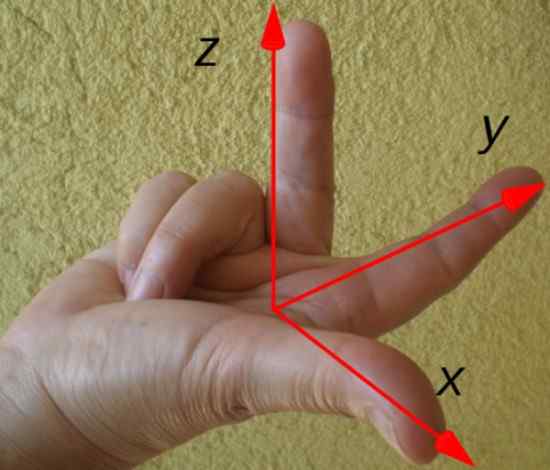Figur 3. Högerhandregel för att bestämma riktningen och riktningen för TROCA. Källa: Wikimedia Commons.

Pekfingret pekar enligt positionsvektorn r, Långfingret enligt kraft F Och tummen signalerar vridmomentets riktning och riktning τ. I det här exemplet riktas vridmomentet längs X -axeln, enligt ritningen av koordinataxlarna.

Formler och ekvationer

Om vridmomenten verkar på en kropp τ₁, τ_2, τ_{3 ..} τ_Yo, Nätet eller resulterande vridmoment τ_n Det är vektor summan av dem alla:

τ_n = τ₁+ τ₂ +  τ₃ +_.. τ_Yo

Med sammanfattning av sammanfattningen kvarstår det:

τ_n = ∑ τ_Yo

Jämviktstillståndet uttrycks matematiskt på följande sätt:

τ_n = 0

Nåväl:

∑ τ_Yo = 0

Där vridmomentet τ, När det gäller en viss O -axel beräknas den av:

τ = r x F

Och vars storlek är:

τ = r⋅f⋅sen θ

Exempel

-Hos människor och djur är vikt en kraft som kan orsaka vridmoment och svänga och falla.

Människor behåller vanligtvis en sådan position att när de går, håller dem i rotationsbalans, såvida inte sportaktivitet utövas, till exempel gymnastik, skridskoåkning eller sport i allmänhet.

-Två barn som lyckades hålla sig horisontella i vagnare antingen upp och ner De är i rotationsbalans.

-När balansen i balansen är balanserad är systemet i rotationsjämvikt.

-Meddelanden och trafikljus som hänger på gator och vägar är också i rotationsbalans. Om kablarna som håller dem är trasiga går denna saldo förlorad och meddelandet hänger eller faller.

Det kan tjäna dig: genomsnittlig acceleration: hur det beräknas och löses

-Hängande broar som Golden Gate i San Francisco och bron i figur 1.

Träning löst

Baren som stöds av ett stöd som visas i figuren är mycket lätt. Den kraft som utövas av stöd är F Och i slutet tillämpar kraften TILL.

Det uppmanas att beräkna storleken på dessa krafter med tanke på att systemet är i balans mellan översättning och rotation.

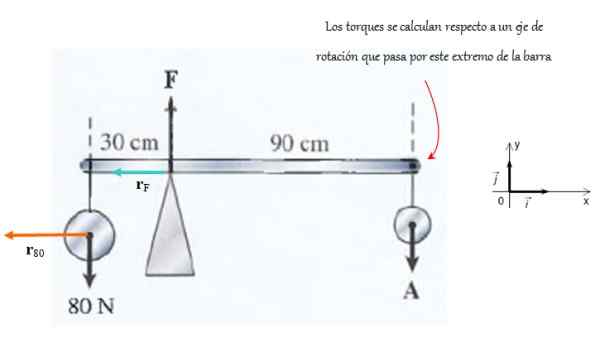Figur 4. På denna bar styrkor agerar på ett sådant sätt att den förblir i rotationsjämvikt. Källa: f. Zapata.

Lösning

Eftersom systemet inte rör sig avbryts summan av krafter. Alla är vertikala och du kan arbeta med storleken. Den positiva känslan är upp och den negativa ner, därför:

F - 80 - A = 0

Nu appliceras rotationsjämviktstillståndet, för vilket du måste välja en godtycklig rotationsaxel. I det här fallet väljs det i slutet till höger, så att vektorn r_TILL Vara noll, på detta sätt som vridmomentet utövas av TILL, men bara de av F och vänsterens styrka.

Det vridmoment som produceras av F Det är enligt regeln för höger hand och koordinatsystemet som visas:

τ_F = r_F x F = 0.9 f (-k) N.m

Det är riktat på skärmen och har ett negativt tecken. Medan vridmomentet som produceras av kraften på 80 N är:

τ = 80 x 1.tjugo (k) N⋅m = 96 (k) N⋅m

Detta vridmoment riktas ut ur skärmen och tilldelas ett positivt tecken. Eftersom det finns rotationsbalans:

96 - 0.9⋅f = 0

Storleken på F är:

F = (96/0.9) n = 106.7 n

Och eftersom systemet är i översättningsbalansen avbryts summan av krafterna. Detta gör att vi kan rensa storleken på TILL:

F - A - 80 N = 0

Därför:

A = 106.7 - 80 n = 26.7 n.

Referenser

1. Rex, a. 2011. Fysikens grunder. Pearson.
2. Serway, R., Jewett, J. (2008). Fysik för vetenskap och teknik. Volym 1. 7th. Ed. Cengage Learning.
3. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14th. Ed. Volym 1. Pearson.
4. Tipler, s. (2006) Fysik för vetenskap och teknik. 5: e upplagan. Volym 1. Redaktör.
5. Tippens, s. 2011. Fysik: koncept och applikationer. Sjunde upplagan. McGraw Hill.