Fraktioner typer, exempel, övningar löst

De bråk antingen bråknummer Det är de siffror som representeras som indikerar kvoten mellan två heltal till och b, så länge som b skiljer sig från 0. Till exempel är 1/3 en bråkdel som läser som "en tredjedel".

Till numret till Det är känt som täljare av bråk och b som nämnare Av samma. Nämnaren anger i hur många delar hela måste delas upp. För sin del indikerar telleren hur många delar av den hela.

Figur 1. Hur många portioner har den här chokladkakaen? Källa: Piqsels.

Det hela är allt som vill dela eller bråk, till exempel en pizza eller chokladstången som visas i figur 1. Baren är gjord på ett sådant sätt att det är mycket lätt att dela upp den i 5 lika delar, där varje del är lika med 1/5 av hela baren.

I fraktion eller fraktionering nummer 1/5 är telleren värd 1 och nämnaren är värd 5. Fraktionen läser "en femte".

Anta att vi äter 3 chokladbitar. Vi skulle säga att vi har ätit 3/5 delar av baren och 2/5 delar är kvar att dela med en vän. Vi kan också säga att vi åt "tre femtedel av choklad" och ge "två femtedelar" till vänen.

Den grafiska representationen av dessa fraktionella nummer är som följer:

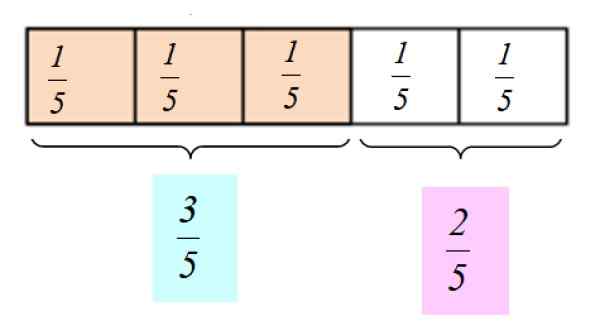figur 2.- Grafisk representation av fraktionerna 3/5 och 2/5. Källa: f. Zapata.

[TOC]

Typer av bråk

Egna bråk

En bråkdel är sin egen när telleren är mindre än nämnaren och därmed är dess värde mindre än 1. Fraktionerna i föregående avsnitt, i exemplet med choklad, är deras egna fraktioner.

Andra exempel på sina egna fraktioner är: ½; 8/10; 3/4 och mer.

Figur 3.- Både 1/4 och 1/2 är deras egna fraktioner. Källa: Wikimedia Commons.

Felaktiga fraktioner

Tecknaren av felaktiga fraktioner är större än telleren. Till exempel tillhör 4/3 8/5, 21/10 till denna kategori.

Uppenbara bråk

Dessa fraktioner representerar ett helt nummer. Bland dem är 4/2, 10/5 och 27/3, eftersom om vi ser bra ut ger resultatet av att dela teller mellan nämnaren av dessa fraktioner ett heltalsnummer.

Således: 4/2 = 2, 10/5 = 2 och 27/3 = 9.

Motsvarande bråk

Två fraktioner N/M och P/Q är likvärdiga vid delning av teller mellan nämnaren. Samma mängd erhålls. På detta sätt representerar motsvarande fraktioner samma del av helheten.

Som ett exempel har vi fraktioner: 15/2 och 30/4. Genom att dela 15 med 2 får du 7.5, men det är också detsamma om 30 är uppdelat med 4.

Kan tjäna dig: injektiv funktion: vad den består av, vad är det för och exempel

För att veta om två fraktioner N/M och P/Q är likvärdiga, verifieras efterlevnaden av följande jämlikhet:

N*q = m.p

Oreducerbara bråk

När telleren och nämnaren är uppdelad både av samma siffra och så länge resultatet är hel, erhålls en bråkdel som motsvarar originalet, men med mindre antal.

Denna process fortsätter medan telleren och nämnaren har samma exakta divisor. När det inte är möjligt att fortsätta dela är att Oåterkallelig fraktion av den ursprungliga fraktionen.

Fördelen som måste arbeta med den oåterkalleliga fraktionen är att en motsvarande fraktion erhålls men med mindre antal. Det är därför du måste se till att minska dem när det är möjligt när du arbetar med fraktioner när det är möjligt, för att underlätta beräkningar.

Anta att fraktion 12/20, som är teller och nämnarpar, kan båda delas med 2:

12/20 = 6/10

Och en gång till:

6/10 = 3/5

3/5 -fraktionen motsvarar 12/20, men enklare.

Siffror

En felaktig fraktion medger också representation som ett blandat nummer, kallad så eftersom det har en hel del och en annan fraktionerad del, den fraktionella delen är en egen bråkdel.

Låt oss titta på ett snabbt exempel med fraktion 15/2 som vi vet motsvarar 7.5.

Vi kan uttrycka till 15/2 som ett blandat nummer som detta:

15/2 = 7 + 0.5

Men 0.5 = ½. Därför 15/2 = 7½ som läser "Seven and a Medium".

Exempel på bråk

Fraktionella nummer är nödvändiga eftersom både naturliga och heltal är otillräckliga när vi vill dela saker som chokladkaketen.

Och det är därför det finns en oändlig variation av mätmönster och objekt vars specifikationer inkluderar fraktionella nummer, för att inte tala om mängden vardagliga situationer där dessa är nödvändiga.

Matköp

I länder där decimalmetriska systemet används är användningen av kilo vanligt att hänvisa till vikten av många livsmedel. Vi vill inte alltid köpa hela belopp, men lite mer eller lite mindre.

Det är därför vi frågar:

• ½ kg fisk
• ¾ kg tomater
• ¼ kilo lök
• 1 ½ kg persikor (1 och ett halvt kilo).

Och när du använder Anglo -Saxon -mätmönstren händer detsamma: vi behöver 2 och ett halvt kilo eller 1/4 av en sak av något.

Kan tjäna dig: Utvärdering av funktioner

Alla dessa siffror är fraktionerade och som vi har sett motsvarar de två olika typer av fraktioner: äger och felaktiga.

Köksrecept

Kökrecept använder ofta bråknummer för att ange antalet vissa ingredienser. Till exempel:

• ½ kopp mjöl
• ¾ kg socker för att förbereda en kaka.

Längder och diametrar

Möbeldimensioner, textilstycken och alla typer av inhemska redskap mäts i tunnelbana eller tumfraktioner, oavsett om det decimala metriska systemet för mått eller anglo -saxon används.

Även i länder där decimalmetriska systemet råder, kommer kommersiellt koppar, stål och andra VVS -material vanligtvis att ha diametrar som anges i tum. På samma sätt andra hårdvaruverk som skruvar och muttrar.

Som en tum motsvarar 2.54 cm, vanligtvis dessa bitar, som har mindre diametrar, uttrycks i tumfraktioner.

Mycket vanliga åtgärder för inhemska rör är:

• ½ tum
• ¼ tum
• 3/8 och 5/8 tum.

Tidsluckor

Dagligen används fraktionella siffror för att uttrycka tidsintervaller som ¼, ½ och ¾ timme, eller till och med lite större: 1 timme och ¼ och så vidare.

Figur 4. De är halvt elva på den här handklockan. Källa: Pixabay.

Övningar med bråk

- Övning 1

Idag har Juanito tagit en tårta till sin födelsedag till skolan och vill distribuera den bland alla sina vänner, men läraren vill ge en bit som är tre gånger större med avseende på barnens.

Med hänsyn till att det finns 24 barn + läraren, till vilken han vill ge motsvarande tre stycken, hur många bitar ska kakan klippa?

Lösning

Om Juanito bara ville distribuera kakan bland sina vänner, skulle var och en motsvara 1/24.

Men eftersom läraren vill ge en del och att stycket är tre gånger större, skulle jag behöva distribuera kakan bland 24 elever + 3 stycken för läraren. Det vill säga varje barn motsvarar 1/27 stycken och läraren 3/27 stycken.

Dessutom, om vi minskar fraktionen 3/27 får vi läraren att ta 1/9 del av kakan.

- Övning 2

Ett företag med en chef och tre anställda har 6000 euro i inkomst varje månad. Hur mycket pengar motsvarar varje person om chefen vill hålla hälften av det han vann?

Kan tjäna dig: Rhomboid: Egenskaper, hur man tar ut omkretsen och området

Lösning

Om chefen vill vinna hälften måste han stanna hos 6000/2, vilket gör 3000 €. Av de andra återstående € 3000 är vad de tre anställda ska distribueras. Således vinner varje anställd 3000/3, vilket resulterar i € 1000.

- Övning 3

Hitta den irreducerbara fraktionen av:

a) 12/18 och b) 4/11

Lösning till

I det första fallet märkte vi att både telleren och nämnaren är jämn och delbar mellan 2. De är också delbara mellan 3, eftersom 12 och 18 är multiplar av den figuren.

Så vi kan förenkla fraktionen genom att dela både telleren och nämnaren antingen mellan 2 eller 3, ordningen är likgiltig.

Börjar med att dela med 2:

12/18 = 6/9

Nu märker vi att både telleren och nämnaren för denna motsvarande fraktion är multiplar av 3, så att dela båda mellan denna figur:

6/9 = 2/3

Och eftersom 2 och 3 är primtal har de inte längre någon annan gemensam delare utom 1. Vi har nått den irreducerbara fraktionen.

Den maximala vanliga MCD -divisorn av telleren och nämnaren kunde också ha beräknats. För 12 och 18:

MCD (12,18) = 6.

Och sedan delas teller och nämnaren med detta nummer, vilket motsvarar det i steg.

Lösning B

Här observerar vi att 11 är ett primtal och dess delare är 1 och 11. För sin del medger 4 som delare till 4, 2 och 1. Förutom 1 har dessa siffror inte en gemensam divisor och därför är fraktionen 4/11 oåterkallelig.

- Övning 4

Ange vilken som är den största fraktionen för varje par:

a) ¾ och 5/4

b) 3/7 och 4/9

Lösning till

När två positiva fraktioner har samma nämnare är den största en som har den största telleren. Därför är 5/4 större, sedan 5> 3.

Lösning B

Om fraktioner N/M och P/Q har en annan nämnar och båda är positiva, är jämförelsekriterierna som följer:

Utan.q> m. P, då n/m> p/q

Ett annat alternativ är att hitta decimaluttrycket för varje fraktion och jämföra.

Enligt det första kriteriet: n = 3, m = 7, p = 4, q = 9. Därför: n.Q = 3*4 = 12 och m.P = 7*4 = 28.

Som 12< 28, ocurre que 3/7 < 4/9.

Eller så uttrycker vi varje bråk som decimal och får detta:

3/7 = 0.428571428 .. .

4/9 = 0.444444444 .. .

De hängande punkterna indikerar att mängden decimaler är oändlig. Men detta räcker för att verifiera att 4/9> 3/7 faktiskt.

Referenser

1. Baldor, a. 1986. Aritmetisk. Codex -utgåvor och distributioner.
2. Carena, m. 2019. Matematikmanual. National University of the Coast.
3. Figuera, J. 2000. Matematik 8. Co-bo-utgåvor.
4. Jiménez, r. 2008. Algebra. Prentice hall.
5. Matematiksidan. Vad är en bråkdel? Återhämtat sig från: themathpage.com.