Växande funktion hur man identifierar det, exempel, övningar

Du har en växande funktion När värdet på y ökar om X också ökar, i motsats till de minskande funktionerna, där värdet på och minskar när X ökar.

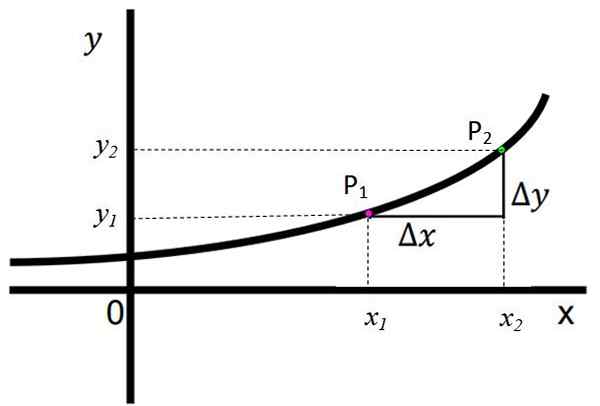
Följande figur visar en växande funktion, och det observeras tydligt att när man flyttar från vänster till höger på x -axeln ökar värdet på respektive koordinat och motsvarande f (x) gradvis. Det sägs att om för allt x₂ > x₁, Då finns det och₂ > och₁.

Figur 1. En växande funktion. Källa: f. Zapata.

Poängen s₁ Och s₂ De visas, de har respektive koordinater (x₁, och₁) och (x₂,och₂). De definieras:

Δy = y₂ -och₁

Δx = x₂ -x₁

I den här funktionen har både ΔY och ΔX ett positivt tecken, vilket betyder det och₂ > och₁ och x₂ > x₁, respektive. Detta är ett tydligt tecken på att funktionen effektivt växer.

Ett bra exempel på alltid växande funktion (ökande monoton) är den neperiska logaritmen för ett riktigt nummer. Ju högre antal, desto större är logaritm.

[TOC]

Hur man identifierar en växande funktion?

I en enkel och kontinuerlig funktion som visas i figur 1 är det lätt att bestämma om funktionen ökar eller minskar, förutsatt att grafen är tillgänglig.

Men mer komplexa funktioner kan växa i vissa intervaller och minska i andra. Det är därför vi pratar om Tillväxtintervall och minska av en funktion.

I nätverket finns det gratis onlinegrafik, till exempel Geogebra, som tillåter grafering av alla typer av funktioner. Med grafen är det lätt att bestämma om funktionen alltid ökar, till exempel f (x) = log x eller om den har intervaller där den växer och andra där den minskar och vad som är.

Det första derivatet

Med tanke på ett visst numeriskt intervall I, om kvoten mellan mängder ΔY och ΔX är positiv, ökar funktionen. Och tvärtom, om det är negativt, minskar funktionen.

Det kan tjäna dig: frekvens sannolikhet: koncept, hur det beräknas och exempel

Du måste:

Δy / Δx> 0 → växande funktion

Det faktum att Δy / Δx> 0 och funktionen ökar i ett visst intervall antyder att den första härrörande från funktionen, eller snarare dess tecken, kan användas som ett kriterium för att avgöra om funktionen i själva verket växer i en viss intervall eller till och med vid en viss punkt i din domän.

Det första derivatet definieras faktiskt som lutningen för kurvan varje punkt:

Vilket innebär att Δx kan göras så liten som du vill. Om f '(x)> 0 för ett visst värde på x, till exempel x = a, är lutningen på kurvan vid den punkten f' (a) positiv och funktionen kommer att öka där.

Följande sats erbjuder ett kriterium för att veta när en funktion växer i intervallet (a, b):

Sats

Låt f (x) vara en härledbar funktion i (a, b). Om f '(x)> 0, för något värde på x som tillhör nämnda intervall, sägs det att f (x) växer i (a, b).

Satsen tillämpas för att ta reda på i vilka intervaller funktionen växer, efter dessa steg:

Steg 1

Hitta de punkter som f '(x) = 0, liksom de där f' (x) inte finns. Dessa kallas kritiska punkter, Detta är punkter där f '(x) kan ändra tecken och därför har f (x) möjlighet att gå från att växa till minskande eller vice versa.

Steg 2

Hitta tecknet på f '(x) för godtyckligt värde i vart och ett av de intervaller som bestäms av de punkter som finns i steg 1.

Steg 3

Använd teoremet för att veta om funktionen växer eller inte i varje intervall.

Exempel på växande funktioner

Det finns funktioner som har vissa tillväxtintervall och andra av minskning, men de som visas nedan växer alltid.

Vikt baserat på ålder

Personens vikt sedan den föddes, tills det är ungefär att avsluta tonåren, är nästan alltid en växande funktion av åldern. Spädbarn och barn växer och utvecklas under åren, och sedan, när de når vuxen ålder, förväntas resten av livet upprätthålla en stabil vikt, även om upp- och nedgångarna är mycket frekventa.

Kan tjäna dig: vertikal linje

Logaritmfunktionen

Funktionerna för verklig variabel logaritm neperian f (x) = ln x och decimal logaritm f (x) = log x växer alltid.

Kvadratrotfunktionen för ett verkligt nummer

En annan funktion som alltid växer är kvadratrotfunktionen för ett positivt verkligt nummer:

y = √x

Den relaterade funktionen och linjära funktionen

Den relaterade funktionen:

f (x) = mx + b

Det växer när linjen är positiv lutning. På liknande sätt identitet och linjära funktioner:

f (x) = x och f (x) = yxa, med a> 0

De växer inom hela sin domän.

Den exponentiella funktionen

En exponentiell funktion som f (x) = e^x  Och i allmänhet formulärets funktion:

f (x) = a^x, Med en> 1

De växer inom hela sin domän.

Den potentiella imple -indexfunktionen

De udda exponentens potentiella funktioner, som dessa:

• f (x) = x³
• g (x) = x⁵

De växer alltid.

Övningar

Övning 1

Bestäm i vilka intervaller funktionen som representeras i följande graf ökar:

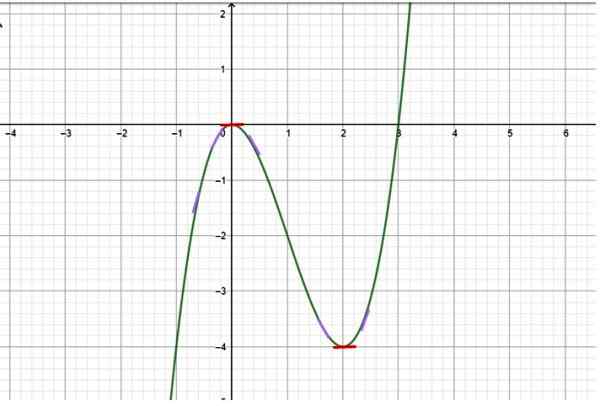figur 2. Funktion med tillväxt och minskning av intervaller. Källa: f. Zapata.

Lösning

Eftersom grafen är tillgänglig bestäms det från sin noggranna observation att funktionen har följande beteende:

-Från x → -∞ till x = 0 ökar funktionen, eftersom värdena på y blir mindre och mindre negativa. Små lutningssegment har ritats i lila för att indikera lutningen på tangentlinjen till kurvan vid olika punkter (lutningen av tangenten till kurvan är just det första derivatet).

Dessa segment har en positiv lutning, så teoremet säkerställer att funktionen växer i detta intervall.

-Men vid x = 0 avbryts kurvens lutning, vilket indikeras med ett litet horisontellt rött segment. Det här är en kritisk punkt av funktionen.

Kan tjäna dig: vad är matematik och vad är de för? 7 viktiga applikationer

Därifrån börjar funktionen att minska och bli mer negativa värdena på och. Denna situation fortsätter tills x = 2, vilket är en annan kritisk punkt.

Sedan minskar funktionen i intervallet från x = 0 till x = 2.

-Från x = 2 blir funktionen mindre och mindre negativ, tills vid x = 3 korsar x -axeln och fortsätter att bli mer positiv varje gång. Därför är detta ett tillväxtintervall.

Slutsats: Tillväxtintervallen är (-∞, 0) och (2, ∞+), medan minskningsintervallet är (0,2).

Övning 2

Bestäm tillväxtintervallen för följande funktion genom kriterierna för det första derivatet:

f (x) = x² - 2x

Lösning

Efter de steg som anges ovan beräknas det första derivatet och är lika med 0 för att hitta de kritiska punkterna:

f '(x) = 2x -2

2x - 2 = 0

x = 1

Detta värde bestämmer förekomsten av intervaller (-∞, 1) och (1, ∞+). Två godtyckliga värden väljs som tillhör var och en:

-För x = 0, som tillhör (-∞, 1), måste du f '(0) = 2.0 - 2 = -2. Eftersom resultatet är negativt minskar funktionen i detta intervall.

-För x = 3, tillhörande (1, ∞+), är det första derivatet värt f '(3) = 2.3 - 2 = 4. Eftersom resultatet är positivt dras slutsatsen att funktionen växer i detta intervall.

Läsaren kan grafera den ursprungliga funktionen f (x) = x² - 2x på en online -grafik för att bekräfta detta resultat.

Referenser

1. Ayres, f. 2000. Beräkning. 5ed. MC Graw Hill.
2. Leithold, L. 1992. Beräkning med analytisk geometri. Harla, s.TILL.
3. Purcell, E. J., Varberg, D., & Rigdon, s. OCH. (2007). Beräkning. Mexiko: Pearson Education.
4. Matemobil. Funktioner, växande, minskande och konstant. Återhämtad från: Matemovil.com
5. Requena, b. Växande funktioner. Återhämtat sig från: universalformulor.com.
6. Stewart, J. 2006. Preccculment: Matematik för beräkning. Femte. Utgåva. Cengage Learning.