Överjektiv funktion, egenskaper, exempel

En överjektivfunktion Det är varje förhållande där varje element som tillhör kodominium är en bild av minst ett domänelement. Även känd som funktion handla om, De är en del av klassificeringen av funktioner angående hur deras element är relaterade.

Till exempel en funktion F: a → B definieras av F (x) = 2x

Som läses "F det går från TILL fram tills B definieras av F (x) = 2x "

Touch Definiera start- och ankomstuppsättningarna A och B.

A: 1, 2, 3, 4, 5 Nu värden eller bilder som vart och ett av dessa element kommer att släppas vid utvärderingen F, De kommer att vara elementen i kodominium.

F (1) = 2

F (2) = 4

F (3) = 6

F (4) = 8

F (5) = 10

Således bildar uppsättningen B: 2, 4, 6, 8, 10

Det kan dras slutsatsen att:

F: 1, 2, 3, 4, 5  → 2, 4, 6, 8, 10 definieras av F (x) = 2x är en överjektiv funktion

Varje element i kodominiet måste vara minst en operation av den oberoende variabeln genom funktionen i fråga. Det finns ingen bildbegränsande, ett element av kodominium kan vara en bild av mer än ett element i domänen och fortsätta att hantera en överjektivfunktion.

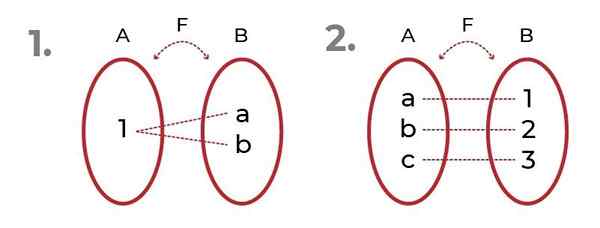
Bilden visar två exempel med onjektivfunktioner.

Källa: Författare

I det första observeras att bilderna kan hänvisas till samma element utan att kompromissa med Överexakivitet av funktionen.

I den andra ser vi en rättvis fördelning mellan domän och bilder. Detta ger upphov till Bijektivfunktion, där kriterierna för Injektionsfunktion och överjektiv funktion.

En annan metod att identifiera onjektivfunktioner, är att verifiera om kodominiet är lika med funktionens rang. Detta innebär att om ankomstuppsättningen är lika med bilderna som tillhandahålls av funktionen vid utvärdering av den oberoende variabeln, Funktionen är överjektiv.

[TOC]

Egenskaper

Att överväga Överdragen Följande måste uppfyllas till en funktion:

Vara F: D_F → C_F

∀ B ℮ C_F  OCH till ℮  D_F   / F (a) = b

Detta är det algebraiska sättet att fastställa det För alla "B" som tillhör c_F Det finns en "A" som tillhör D_F  så att F -funktionen utvärderas i "A" är lika med "B". 

Det kan tjäna dig: radikala egenskaper

Överjektivitet är en egenhet i funktioner, där kodominium och rang är liknande. Således utgör elementen som utvärderas i funktionen ankomstuppsättningen.

Funktionskonditionering

Ibland en funktion som inte är det Överdragen, kan genomgå viss konditionering. Dessa nya förhållanden kan förvandla det till en överjektivfunktion.

Alla typer av modifieringar av funktionen och kodominiet för funktionen är giltiga, där målet är att uppfylla overjektivitetsegenskaperna i motsvarande relation.

Exempel: Löst övningar

Att uppfylla villkoren för Överexakivitet Olika konditioneringstekniker bör tillämpas, detta för att säkerställa att varje element i kodominiet ligger inom uppsättningen av funktionen.

Övning 1

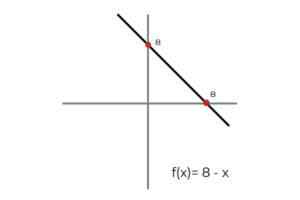
• Vara funktionen F: r → R definieras av linjen F (x) = 8 - x

A: [alla riktiga siffror]

Källa: Författare

I det här fallet beskriver funktionen en kontinuerlig linje, som täcker alla verkliga siffror både inom deras domän och räckvidd. Eftersom funktionens rang R_F Det är lika med kodominium R Det kan dras slutsatsen att:

F: r → R definieras av linjen F (x) = 8 - x är en överjektivfunktion.

Detta gäller alla linjära funktioner (funktioner vars större grad av variabeln är en).

Övning 2

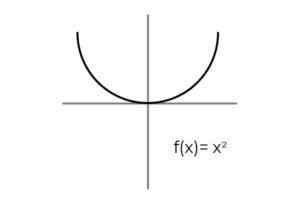
• Studera funktionen F: r → R definieras av F (x) = x² : Definiera om det är en överjektivfunktion. Om det inte är det, visa nödvändig konditionering för att göra det överjektivt.

Källa: Författare

Det första att tänka på är kodominiet för F, som består av verkliga siffror R. Det finns inget sätt för funktionen att kasta negativt värde, vilket utesluter negativa riktiga bland möjliga bilder.

Konditionering av intervallkodominiet [0 , ∞ ]. Det undviks att lämna delar av co -alomio utan att relatera igenom F.

Bilderna upprepas för par av element i den oberoende variabeln, till exempel x = 1 och x = - 1.  Men detta påverkar bara Injicering  av funktionen, som inte är ett problem för denna studie.

Kan tjäna dig: successiva derivat

På detta sätt kan det dras slutsatsen att:

F: r  →[0, ∞ ) definieras av F (x) = x²    Det är en överjektiv funktion

Övning 3

• Definiera villkoren för kodominiet de skulle överdragen till funktioner

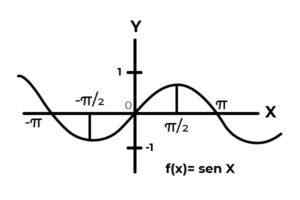
F: r  → R definieras av F (x) = sin (x)

F: r  → R definieras av F (x) = cos (x)

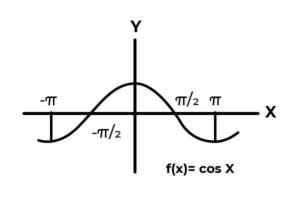Källa: Författare Källa: Författare.

Beteendet hos trigonometriska funktioner liknar vågorna, som är mycket vanligt att hitta repetitioner av den beroende variabeln mellan bilderna. I de flesta fall är funktionen också begränsad till en eller flera sektorer i den verkliga linjen.

Detta är fallet med sinus- och kosinusfunktioner. Där deras värden varierar i intervallet [-1, 1]. Nämnda intervall måste konditionera kodominiet för att uppnå kuvertet för funktionen.

F: r  →[-Eleven] definieras av F (x) = sin (x)  Det är en överjektiv funktion

F: r  →[-Eleven]definieras av F (x) = cos (x) Det är en överjektiv funktion

Övning 4

• Studera funktionen

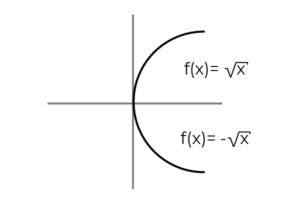
F: [0, ∞ ) → R definieras av F (x) = ± √x   beteckna om det är en överjektivfunktion

Källa: Författare

Funktionen F (x) = ± √x  Det har specialiteten som definierar 2 beroende variabler vid varje värde på "x" . Det vill säga att intervallet får två element för varje som utförs i domänen. Ett positivt och negativt värde för varje värde på "x" måste verifieras för varje värde på "x".

Vid observation av startmonteringen noteras det att domänen redan har begränsats, detta för att undvika de obestämningar som produceras vid utvärdering av ett negativt antal inom en vridmomentrot.

Vid verifiering av funktionen visar det sig att varje kodominiumvärde tillhör sortimentet.

På detta sätt kan det dras slutsatsen att:

F: [0, ∞ ) → R definieras av F (x) = ± √x  Det är en överjektiv funktion

Kan tjäna dig: samtidiga vektorer: egenskaper, exempel och övningar

Övning 4

• Studera funktionen F (x) = ln x  beteckna om det är en överjektivfunktion. Konditionera ankomsten och avgången ställer in för att anpassa funktionen till kriterierna för överjektivitet.

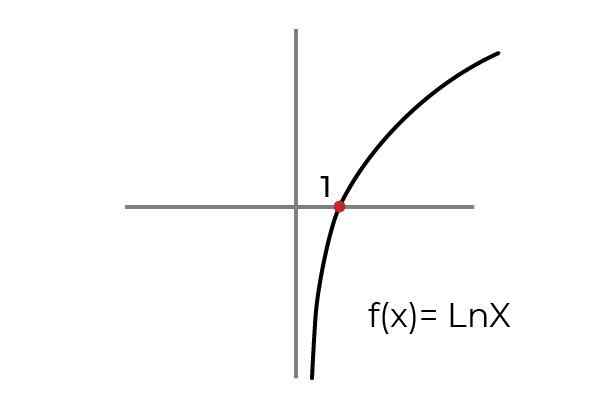Källa: Författare

Som visas i grafen funktionen F (x) = ln xdefinieras för värdena "x" större än noll. Medan värdena på "och" eller bilder kan ta något verkligt värde.

På detta sätt kan vi begränsa domänen för F (x) = till intervallet (0 , ∞ )

Medan funktionens rang kan upprätthållas som uppsättning av verkliga siffror R.

Med tanke på detta kan man dra slutsatsen att:

F: [0, ∞ ) → R definieras av F (x) = ln x  Det är en överjektiv funktion

Övning 5

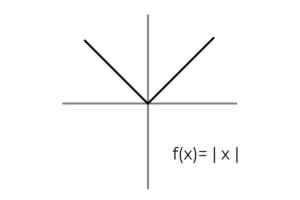
• Studera absolut värdefunktion F (x) = | x | och utse ankomst- och avgångsuppsättningarna som samlas till kriterierna för allegivitet.

Källa: Författare

Funktionens domän uppfylls för alla riktiga siffror R. På detta sätt måste den enda konditioneringen genomföras i kodominiet, med hänsyn till att den absoluta värdefunktionen endast tar positiva värden.

Funktionens kodominium upprättas utjämnar det till området på samma sätt

[0 , ∞ )

Nu kan det dras slutsatsen att:

F: [0, ∞ ) → R definieras av F (x) = | x |  Det är en överjektiv funktion

Föreslagna övningar

1. Kontrollera om följande funktioner är överjektiv:

• F: (0, ∞ ) → R definieras av F (x) = log (x + 1)
• F: r → R definieras av F (x) = x³
• F: r →[1, ∞ )  definieras av F (x) = x²  + 1
• [0, ∞ ) → R definieras av F (x) = log (2x + 3)
• F: r → R definieras av F (x) = sek x
• F: R - 0 → R definieras av F (x) = 1 / x

Referenser

1. Introduktion till logik och kritiskt tänkande. Merrilee h. Lax. University of Pittsburgh
2. Problem i matematisk analys. Piotr Bilar, Alfred Witkowski. University of Wroclaw. Pol.
3. Delar av abstrakt analys. Mícheál O'Searcoid PhD. Institutionen för matematik. University College Dublin, Beldfield, Dublind 4
4.  Introduktion till logik och metodik för de deduktiva vetenskaperna. Alfred Tarski, New York Oxford. Oxford University Press.
5.  Matematiska analysprinciper. Enrique Linés Escardó. Redaktionella återkomster. Till 1991. Barcelona, ​​Spanien.