Analytisk geometri

Vi förklarar vilken analytisk geometri, dess historia, vilka studier och tillämpningar är

Vad är analytisk geometri?

De analytisk geometri Det är grenen av matematik där geometri och algebra kombineras för att lösa olika geometriska problem genom algebraiska tekniker.

Använd koordinatsystem, till exempel det kartesiska koordinatsystemet, som är skyldig sitt namn René Descartes. På detta sätt är det möjligt att associera kurvor i planet och i rymden, med algebraiska ekvationer.

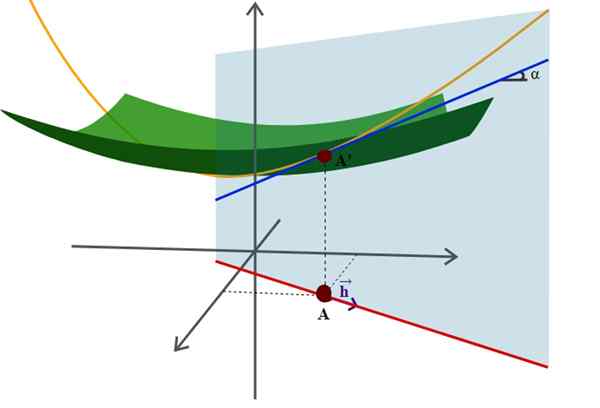
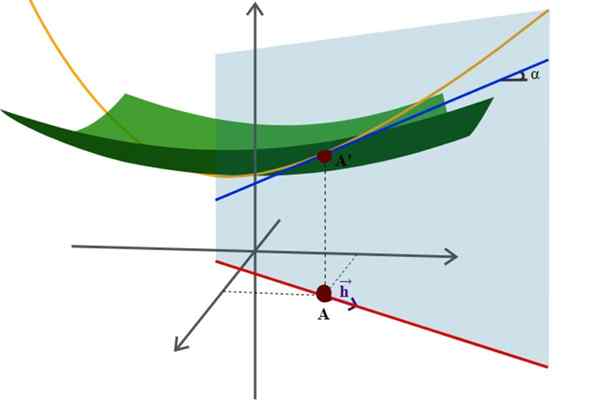Diagram över en yta i rymden och dess riktningsderivat, ett av de många mer avancerade tillämpningarna av analytisk geometri. Källa: Wikimedia Commons.

Ett exempel på detta är den välkända ekvationen för radien r -riortion centrerad på ursprunget till koordinatsystemet:

Utan tvekan är det i många fall enklare att arbeta med det algebraiska uttrycket av en kurva än med dess geometriska representation själv. Detta är fallet vid beräkning av korsningar mellan kurvor eller hitta tangent eller torkningslinjer till dem.

På samma sätt är det genom analytisk geometri möjligt att layoutfunktioner grafik. Och som är känt tillåter funktionerna modellering av vetenskap och tekniska problem. Därför finns analytisk geometri i läroplanerna för de karriärer som är förknippade med dessa kunskapsområden.

Kort historia om analytisk geometri

Analytisk geometri har sitt ursprung under första hälften av 1600-talet, av handen av två anmärkningsvärda franska matematiker: René Descartes (1596-1650) och Pierre de Fermat (1601-1665).

Rene Descartes

Det kan emellertid sägas att hans bakgrundsdatum tillbaka århundraden, till den grekiska matematikern Apollonius i Pergamo (262-190 a.C.). Han skrev en avhandling om Conics, till vilken han beviljade deras namn: omkrets, ellips, liknelse och hyperbola.

Det kan tjäna dig: sammansatt proportionalitet: Förklaring, tre sammansatta regel, övningar

Således var Apollonios arbete grunden för, mycket senare, de franska René Descartes och Pierre de Fermat lägger grunden för analytisk geometri, oberoende. Men Descartes anses vara far till denna vetenskap, eftersom han var den första som publicerade sina verk.

Descartes, Fermat och Euler

I talet från 1637 -metoden förenade Descartes två discipliner som fram till dess hade separerats: Algebra och geometri. I sitt arbete introducerar Descartes det kartesiska koordinatsystemet för att hitta punkter i planet och i rymden.

Det använder sig också av andra -graders algebraiska ekvationer med två variabler, för att beskriva de koniska sektionerna och ägnas åt att lösa geometriska problem med dem. Också för att skapa en bra del av den matematiska notationen som för närvarande används.

Pierre de Fermat är mer associerad med optik än med analytisk geometri, men deras bidrag är anmärkningsvärda.

1629 återupptog Fermat conics of Apollonius of Pergamo och skapade de tekniker som utgör den analytiska geometrien, uppfann sitt eget koordinatsystem och tydligt definiera nyckelkonceptet för Geometrisk plats, med vilken studien av analytisk geometri börjar.

Fermats verk såg emellertid inte ljuset förrän 1679, publicerad av sin son, när matematikern redan hade dött. Av denna anledning tillskrivs faderskapet i analytisk geometri till Descartes.

Därefter etablerade de franska matematikerna, den schweiziska Leonardo Euler (1707-1783) inrättade de formella baserna för analytisk geometri. Euler introducerade flera koordinatsystem i planet och rymden: rektangulära, polära och sneda koordinater, samt transformationer från ett system till ett annat.

Kan tjäna dig: Hur erhålls informationen i en undersökning?

In his works about analytical geometry, Euler also deepened the classification of various curves, according to the degree of the representative algebraic equation (third and fourth order) and studied its properties intensively, the equations of the tangents, the curvatures, The symmetries and much Mer.

Vilka studier analytisk geometri?

I stort sett fokuserar analytisk geometri på studien av geometriska element, såsom punkter, segment, linjer, kurvor, ytor och volymer. För att göra detta, som nämnts ovan, upprättar det algebraiska ekvationer som beskriver och relaterar dessa element, vilket tillåter deras hantering genom algebraiska tekniker.

Huvudmålen för analytisk geometri, på ett mycket sammanfattande sätt, är följande:

1. Upprätta det kartesiska koordinatsystemet och det polära koordinatsystemet för att hitta punkter i planet, liksom dess förlängning till punkter i rymden.
2. Rita segment, raka, kurvor och ytor på det kartesiska planet och rymden.
3. Dra ut ekvationerna som analytiskt beskriver en kurva och konstruktionen av den på planet och/eller rymden, såväl som studien av alla dess egenskaper.
4. Klassificera kurvor, ytor och volymer.
5. Erhålla grundläggande formler för att lösa problem på anmärkningsvärda punkter, raka, planer, vinklar, parallellitet, vinkelräthet, avstånd, korsningar, områden och mer.
6. Lös geometriska problem genom tillämpning av algebraiska metoder, för vilka formler som hänvisar till anmärkningsvärda punkter, ekvationer för linje, planer, vinklar, avstånd mellan punkter, mellan linjer och punkter, tangenspunkter, torra linjer, områden, områden och mycket mer.
7. Arbeta med vektorutrymmen och produkter mellan vektorer.

Avstånd mellan två poäng

Som ett exempel på de många tillämpningarna av analytisk geometri är en av de enklaste beräkningen av avståndet mellan två punkter i planet. Är två punkter P₁ Och s₂, av koordinater (x₁,och₁) och (x₂,och₂) respektive avstånd d mellan dem beräknas av:

Kan tjäna dig: trinomial

Polära koordinater

En planpunkt kan specificeras genom dess "R" -avstånd till koordinatsystemets ursprung, kallad polo, och vinkeln som bildar den linje som innehåller till punkten och polen, med den horisontella axeln eller polära axel.

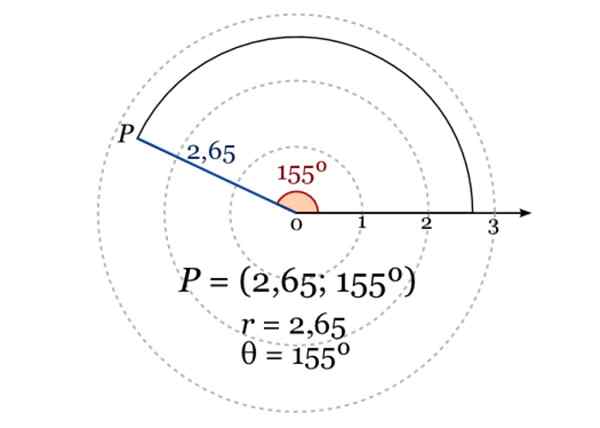Bilden visar de polära koordinaterna för en punkt P, där r = 2.65 och vinkeln i grader med avseende på den polära axeln är 155º. Källa: Wikimedia Commons.

Analytiska geometri -applikationer

Grund av infinitesimal beräkning

Analytisk geometri är avgörande för utvecklingen av infinitesimal beräkning, eftersom den underlättar den grafiska representationen av kurvor och funktioner och arbetar med dem på ett analytiskt sätt, för att skapa modeller som representerar naturfenomen.

Kartor

Det kartesiska koordinatsystemet hjälper till att göra kartor och identifiera platser genom latitud och längd, motsvarande de kartesiska koordinaterna för en punkt i planet.

Topografisk beräkningar

Olika typer av koordinatsystem används i topografi och utgör grunden för deras studie och tillämpningar. Bland dem är det polära koordinatsystemet som beskrivs ovan.

Himmelkroppsbana

De koniska sektionerna, som beskrivs genom analytisk geometri, deltar i viktiga naturfenomen, såsom himmelkroppens banor, med förbehåll för tyngdkraften. Till exempel beskriver planeterna och vissa kometer elliptiska banor runt solen, med detta beläget i en av strålkastarna.

Civil arkitektur och konstruktioner

Många kurvor är en del av de arkitektoniska konstruktionerna, till exempel kan kablarna på en hängande bro ta form av liknelser.

Globala positioneringssystem

Det globala positioneringssystemet eller GPS gör möjliga platser med precision, liksom rörliga föremål, till exempel fordon och båtar. Det hjälper också människor att bli lättare till sina destinationer och vägleda dem på de bästa rutterna.