Heptagon

Ett exempel på heptagon

Vad är en hepagon?

han heptagon Det är en polygon med sju sidor och sju inre vinklar. Som ett geometriskt ord härstammar ordet från det grekiska Hepta, vilket betyder sju, och gonos, Översatt som en vinkel. Det är därför en polygon med sju vinklar.

En polygon är en platt geometrisk figur som bildar och stänger tre eller flera segment, även kallad sidor. De vanliga punkterna som sidorna har kallas Häckar.

Regionen mellan angränsande sidor, på insidan av figuren, är Inre vinkel, vars toppunkt också är en av hepagons toppar.

Om alla sidor och inre vinklar har samma mått är det en regelbunden heptagon, annars är en oregelbunden heptagon. Oregelbundna heptoner adopterar ett stort utbud av former.

En hepagon kan också vara konvex antingen konkav, Enligt måttet på dess inre vinklar. Om de inre vinklarna mäter mindre än 180 ° är hepagon konvex, men om en eller flera av nämnda vinklar överstiger 180 °, är den konkav.

En heptagon vars sidor är alla samma mått kallas Balateral. Detta kan vara konkavt eller konvext, regelbundet eller oregelbundet.

Regelbunden och oregelbunden heptagon

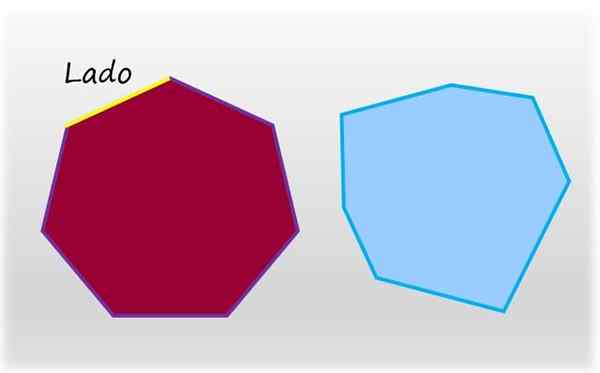Hepagon är den platta och stängda figuren på sju sidor. Till vänster, en regelbunden heptagon, vars sidor och inre vinklar har lika mått. Till höger, en oregelbunden heptagon. Källa: f. Zapata.

Den vanliga heptagon är en som har sina sju sidor och dess sju inre vinklar med lika mått, motsatsen till en oregelbunden heptagon, som har minst en sida av olika mått, eller en annan inre vinkel.

Den vanliga hepagon

Symmetri

En regelbunden heptagon är en mycket symmetrisk figur. Segment kan dras som förbinder ett toppunkt med mittpunkten på motsatt sida, som alla korsar i mitten av hepagon. Dessa är de sju symmetriaxlarna i figuren.

Kan tjäna dig: område med en vanlig och oregelbunden Pentagon: hur det tas, övningar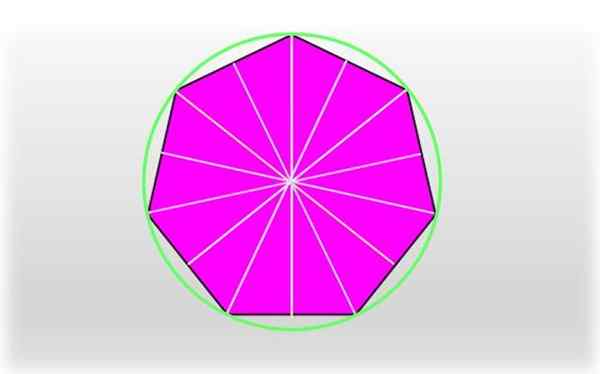 En vanlig heptagon och dess symmetriaxlar. Omkretsen som passerar genom var och en av hepagons hörn kallas omskriven omkrets.

Segmentet som ansluter sig till ett toppunkt i mitten av hepagon kallas Cirkunradio, Det motsvarar radien för den unika omkretsen som passerar genom var och en av vertikalerna, som visas i figuren.

Vinklar

I hepagon sticker följande vinklar:

• Inre vinkel ϕ, vars toppunkt sammanfaller med en av topparna i hepagon, som är sidorna på vinkeln, två av de intilliggande sidorna av hepagon. För en regelbunden heptagon är måttet på var och en av de sju inre vinklarna ungefär 128.57 °.
• Yttre vinkel, den som bildas mellan en av sidorna och förlängningen av en av de angränsande sidorna, som är det vanliga toppunktet mellan dessa två sidor. På samma sätt bildas sju yttre vinklar och deras värde beräknas genom att subtrahera 180 ° från den inre vinkeln, som för den regelbundna hepagon, resulterar i 51.43 °.
• Centralvinkel θ, Den har sitt toppunkt i mitten av den vanliga heptgon. Det beräknas genom att dela 360 ° med 7, vilket resulterar i ungefär 51.43 °.

Summan av den inre vinkeln och den centrala vinkeln är lika med 180 °, det vill säga:

ϕ + θ = π

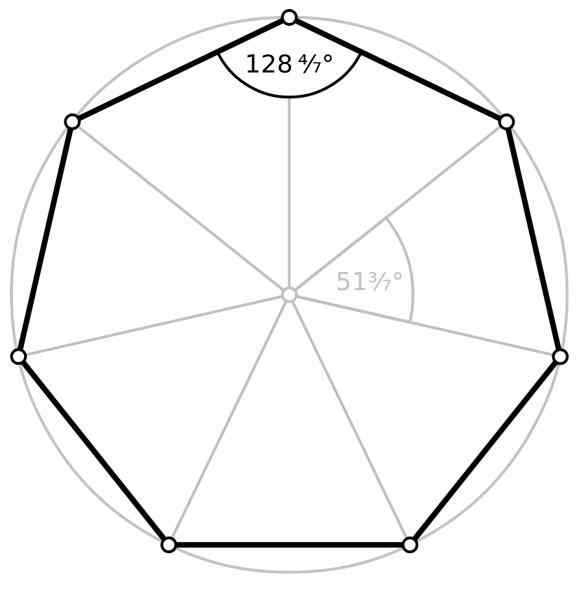Inre vinkel och central vinkel på den vanliga hepagon. Källa: Wikimedia Commons

Område

För den vanliga hepagon finns formler, medan du för den oregelbundna hepagon måste ta till andra metoder, till exempel att dela upp den i andra enklare polygoner, till exempel trianglar.

Det kan tjäna dig: regel t: egenskaper, så att det är exempel

Regelbundet heptagonområde

1. Om omkretsen p och apotemet till_p:

Vare sig det till hepagon -området. Det finns en formel för att beräkna området, giltigt för regelbunden polygon:

2. Om L och apotem är kända till_p:

Eftersom omkretsen är summan av sidorna, och sidan mäter l i den vanliga hepagon, erhålls den:

P = 7⋅l

Ersätter i den tidigare formeln:

3. Om sidan är känd        

Följande är en ungefärlig, giltig formel när måttet på hepagon är känd:

A = 3.634 ∙ l²

Oregelbundet heptagonområde

Det oregelbundna heptagonområdet kan beräknas av triangulering, som består av att dela hepagon i fem trianglar (se följande figur). Området för var och en beräknas och resultaten läggs till, vilket får det kompletta området för hepagon.

Den andra metoden kallas Gauss determinant, Och det är nödvändigt att placera hepagon i ett rektangulärt koordinatsystem för att veta koordinaterna för varje toppunkt. Området beräknas av en formel som involverar värdena på dessa koordinater.

Diagonaler

De diagonaler Det är segment som förbinder ett toppunkt till en annan som inte är i följd (om segmentet ansluter två på varandra följande vertikaler är sida). En heptagon har totalt 14 diagonaler.

Antalet diagonaler D för en vilken polygon som helst, beräknas genom formeln:

D = n · (n - 3) / 2

Ersätta n = 7, återstår:

D = 7 · (7 - 3) / 2 = 7 · (4/2) = 14

Summan av inre vinklar

För alla heptagon, oavsett om det är regelbundet, är summan av dess inre vinklar lika med 900 ° eller 5π radianer.

Det kan tjäna dig: trigonometriska skäl: exempel, övningar och applikationer

Den här egenskapen är mycket lätt att demonstrera, för detta är hepagon uppdelad i enskilda trianglar som inte överlappar varandra och drar rätlinjiga segment som förenar vertikalerna, utan att korsa varandra.

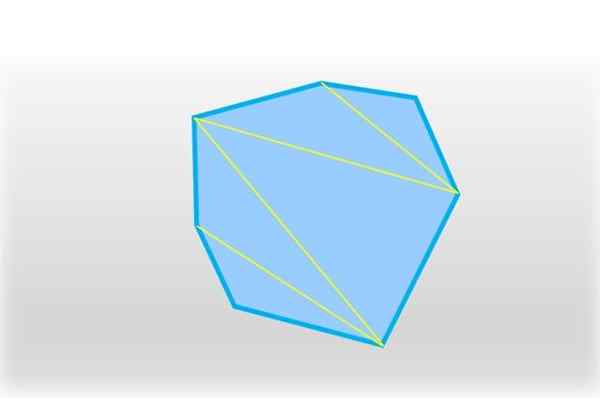En hepagon kan delas upp i fem trianglar, som går med ett segment två icke -konsekutiva hörn. Källa: f. Zapata.

Fem trianglar erhålls och i var och en är summan av dess inre vinklar 180 °, vilket multipliceras med 5 är lika med 900 °:

5 x 180 ° = 900 °

Formler

Omkrets

För en regelbunden heptagon från L beräknas omkrets P enligt följande:

P = 7⋅l

Om omkretsen är oregelbunden läggs längderna på var och en av de sju sidorna.

Inre vinkelmått

I en regelbunden heptagon mäter den inre vinkeln θ:

θ = [180 (n-2)]/n

Där n = 7.

Apotem

Vara l på sidan av den vanliga hepagon. Apotemet är det segment som går från mitten av hepagon, vinkelrätt till motsatt sida.

Låt a_p Apotemens längd. Att känna till radien för den omskrivna omkretsen, som betecknas som r_c Och l -sidan av hepagon, du har:

Genom att känna till den inre vinkeln θ är ovanstående ekvivalent med:

Område

Om det är en vanlig heptagon från L ges området A av:

A = 3.634 ∙ l²

När hepagon är oregelbunden behövs de rektangulära koordinaterna för varje toppunkt, ges av (x_n , och_n), Där n = 1, 2, 3 ... 7.

Sedan tillämpas följande formel för att hitta område A:

Diagonaler

Numret D av diagonaler ges av:

D = n · (n - 3) / 2

Där n = 7 för hepagon.

Hur man gör en heptagon

Följande animation visar hur man ritar ungefär en regelbunden hepagon, med regel och kompass.

Konstruktion av den vanliga hepagon. Källa: Wikimedia Commons

Referenser

1. Alexander, D. 2013. Geometri. Femte. Utgåva. Cengage Learning.
2. Lemonis, m. Regelbunden Hepalle -kalkylator. Återhämtat sig från: calcresource.com.
3. Matematik öppen referens. Polygonområde. Återhämtat sig från: MathPenref.com.
4. Universumsformler. Heptagon. Återhämtat sig från: universalformulor.com.
5. Wikipedia. Heptagon. Återhämtad från: är.Wikipedia.com.