Hypercubo -definition, dimensioner, koordinater, utspelade

En hyperkub är en dimension kub n. Det speciella fallet med dimension Hypercubo kallas Tester. En hypercubo eller n-kub består av raka segment, alla samma längd som är ortogonala i deras vertikaler.

Människor uppfattar det tre dimensionella utrymmet: brett, högt och djup, men det är inte möjligt för oss att visualisera en hyperkub av dimension större än 3. 

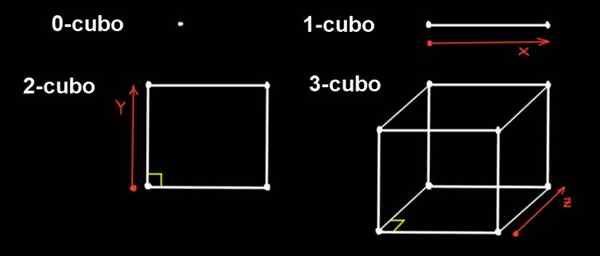
Figur 1. En 0-kub är en punkt, om den punkten sträcker sig i en riktning ett avstånd på ett 1-kubo sätt, om den 1-kubo sträcker sig ett avstånd till i ortogonal riktning finns det en 2-kub (från sidor till x a), Om 2-kuben sträcker sig ett avstånd till i ortogonal riktning finns det en 3-kubo. Källa: f. Zapata.

Vi kan göra prognoser i det tre dimensionella utrymmet för att representera det, liknande hur vi projicerar en kub på ett plan för att representera det.

I dimension 0 är den enda siffran poängen, så en 0-kub är en punkt. En 1-kub är ett rak segment, som bildas genom att flytta en punkt på avstånd till ett avstånd till.

För sin del är en 2-kub en fyrkant. Det är byggt genom att förskjuta 1-kuben (segmentet långt a) i riktningen och, som är ortogonal till X-adressen, ett avstånd till.

3-kuben är den vanliga kuben. Den är byggd av fyrkanten som förskjuter samma i den tredje riktningen (z), som är ortogonal för X- och Y -riktningarna, ett avstånd till.

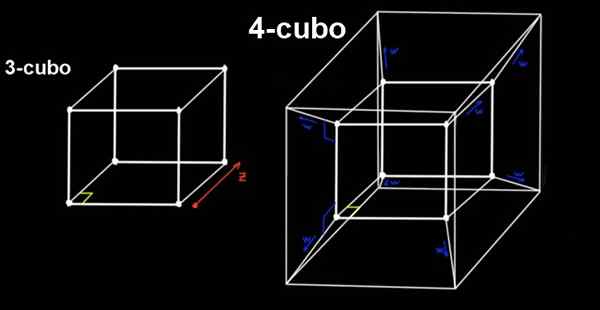figur 2. En 4-kubo (testeract) är förlängningen av en 3-kub i ortogonal riktning till de tre konventionella rumsliga adresserna. Källa: f. Zapata.

4-kuben är rättegången, som är byggd av en 3-kubo som förskjuter samma ortogonalt, ett avstånd till, mot en fjärde dimension (eller fjärde riktningen), som vi inte kan uppfatta.

En trigger har alla sina raka vinklar, den har 16 vertikaler och alla dess kanter (totalt 18) har samma längd till.

Om längden på kanterna på en n-kub eller hypercubo av dimension n är 1, är det en enhet Hypercubo, där de längsta diagonala mätningarna √n.

Kan tjäna dig: linjär programmering: vad är det för, modeller, begränsningar, applikationerFigur 3. En n-kub erhålls från en (n-1) -CUBO som utvidgar den ortogonalt i nästa dimension. Källa: Wikimedia Commons.

[TOC]

Vilka är dimensionerna??

Dimensionerna är frihetsgraderna eller de möjliga riktningarna där ett objekt kan röra sig.

I dimension 0 finns det ingen möjlighet att röra sig och det enda möjliga geometriska objektet är poängen.

En dimension i det euklidiska utrymmet representeras av en orienterad linje eller axel som definierar den dimensionen, kallad X -axeln. Separationen mellan två punkter A och B är det euklidiska avståndet:

D = √ [(x_till - x_b)²]. 

I två dimensioner representeras utrymmet av två ortogonala orienterade linjer med varandra, kallad X och Axis.

Positionen för vilken punkt som helst i detta två dimensionella utrymme ges av dess par av kartesiska koordinater (x, y) och avståndet mellan två punkter a och b alla kommer att vara:

D = √ [(x_till - x_b)² + (och_till - och_b)²]

Eftersom det är ett utrymme där euklidgeometri är uppfylld.

Det tre dimensionella utrymmet

Tre -dimensionellt utrymme är utrymmet där vi rör oss. Den har tre riktningar: bredd, hög och djup.

I ett tomt rum ger de vinkelräta hörnen med varandra dessa tre riktningar och till var och en kan vi associera en axel: x, y, z.

Detta utrymme är också Euklidian och avståndet mellan två punkter A och B beräknas enligt följande:

D = √ [(x_till - x_b)² + (och_till - och_b)² + (z_till - z_b)²]

Människor kan inte uppfatta mer än tre rumsliga dimensioner (eller Euclideas).

Men från den strikt matematiska synvinkeln är det möjligt.

I detta utrymme har en punkt koordinater: (x1, x2, x3, ..., xn) och avståndet mellan två punkter är: 

D = √ [(x_Första - x_{1 b})² + (x_{2: a} - x_2B)² +... + (x_na - x_Bent)²].

Kan tjäna dig: hypergeometrisk distribution: formler, ekvationer, modell

Den fjärde dimensionen och tiden

I teorin om relativitet behandlas faktiskt som ytterligare en dimension och en koordinat är associerad.

Men det måste klargöras att denna koordinat som är förknippad med tiden är ett imaginärt antal. Därför är separationen av två punkter eller händelser i rymdtiden inte euklidiana, utan följer Lorentz-metriken.

En fyrdimensionell hypercubo (avtryckaren) lever inte i rymdtid, tillhör en fyrdimensionell euklideal hyper-rymd. 

Figur 4. 3D -projektion av en fyra -dimensionell hypercubo i enkel rotation runt ett plan som delar framfiguren till vänster, tillbaka till höger och från topp till botten. Källa: Wikimedia Commons.

Koordinaterna för en hypercubo

Koordinaterna för vertikalerna för en N-kubo centrerad på ursprunget uppnås genom att göra alla möjliga permutationer av följande uttryck:

(A/2) (± 1, ± 1, ± 1, .. ., ± 1)

Där a är kanten på kanten.

-han volym Från en kant av kanten A är: (a/2)ⁿ (2ⁿ) = aⁿ.

-De längsta diagonal Det är avståndet mellan motsatta vertikaler.

-Följande är motsatta vertikaler på en fyrkant: (-1, -1) och (+1, +1).

-Och i en Kub: (-1, -1, -1) och (+1, +1, +1). 

-De längsta diagonal av ett N-Cubo-mått: 

D = √ [1 -(-1))² +... + (1 -(-1))²] = √ [n 2²] = 2√n

I detta fall antogs det att sidan är a = 2. För en N-Cubo-sida kommer någon att stanna kvar:

d = a√n.

-En försök har var och en av sina 16 vertikaler anslutna till fyra kanter. Följande figur visar hur vertikalerna är anslutna i en trigger.

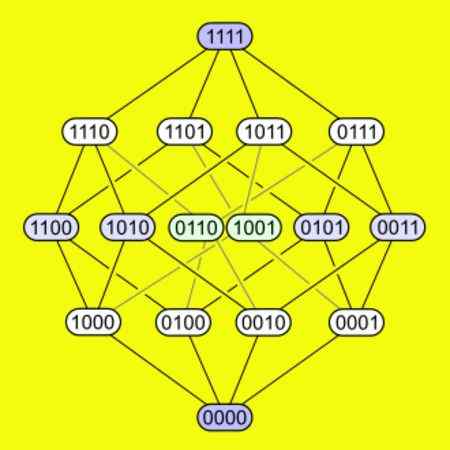Figur 5. De 16 vertikalerna i en fyrdimensionell hypercubo visas och hur de ansluter samma. Källa: Wikimedia Commons.

Utfoldad av en hypercubo

En regelbunden geometrisk figur, till exempel en polyhedron, kan utvecklas i flera lägre dimensionalitetsfigurer.

När det gäller en 2-kubo (en fyrkant) kan utvecklas i fyra segment, det vill säga fyra 1-kubo.

Det kan tjäna dig: Poisson -distribution: formler, ekvationer, modell, egenskaper

På liknande sätt kan en 3-kubo utvecklas i sex 2-kubo.

Figur 6. En n-kub kan utvecklas i flera (n-1) -cubos. Källa: Wikimedia Commons.

En 4-kubo (testeract) kan utvecklas i åtta 3-kubo.

Följande animation visar utbredningen av en tripe.

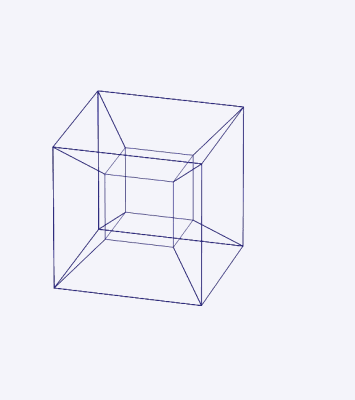Figur 7. En 4 -dimensionell hypercubo kan utvecklas i åtta tre dimensionella kuber. Källa: Wikimedia Commons. Figur 8. Tre -dimensionell projektion av en fyrdimensionell hypercubo som gör en dubbel rotation runt två ortogonala plan. Källa: Wikimedia Commons.

Referenser

1. Vetenskaplig kultur. Hypercubo, visualisering av den fjärde dimensionen. Hämtad från: Culturecientifica.com
2. Epsiloner. Tetradimensionell hypercubo eller tesseract. Återhämtat sig från: epsilones.com
3. Perez R, Aguilera A. En metod för att få en försök från utvecklingen av en hypercubo (4D). Återhämtat sig från: forskning.netto
4. Wikilibros. Matematik, polyhedra, hypercubes. Återhämtad från: är.Wikibooks.org
5. Wikipedia.  Hyperkub. Hämtad från: i.Wikipedia.com
6. Wikipedia. Tesseract. Hämtad från: i.Wikipedia.com