Lagrange interpolation

Vad är Lagranges interpolation?

Lagranges interpolering är en numerisk metod för tillnärmning av funktioner, som använder sig av ett polynom som passerar genom vissa kända punkter i funktionen som är avsedd att ungefärliga.

Om den ungefärliga funktionen är mjuk, även utanför de givna eller kända värdena, tar polynomet värden nära de av intresse av intresse, särskilt om dessa värden är mellan de givna punkterna. Det är därför polynom anses vara en bra strategi för funktionen.

Figur 1.- Formel för att bygga Lagrange -polynomer. Källa: f. Zapata.

Anta nu att du vill närma dig en funktion f (x) varav bara deras värden är kända i vissa x-_Yo-, med Yo från 0 fram tills N-1. Det vill säga de känner varandra n punkter (x-_Yo, och_Yo) med och_Yo = f (x_Yo), Där indexet Yo Går från 0 fram tills N-1.

I Lagrange -interpoleringsmetoden, polynomet som närmar sig funktionen f (x) Det är ett polynom P (x) grad N-1, byggd av den linjära kombinationen av n Polynomer L_Yo(x) grad N-1. Dessa är Lagrange polynomer, som uttrycks enligt följande:

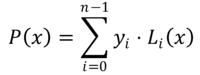
Värdena på och_Yo De representerar ordinaterna som motsvarar abscissen x_Yo Där funktionen f (x) Det är känt, det vill säga: och_Yo = f (x_Yo).

Lagrange polynomer

Genom linjära kombinationer mellan dem fungerar LaGrange -polynomer som en grund för att bygga klass Polynomial N -1 som kommer att tjäna till att interpolera n Kända punkter.

Notationen för polynomer är l_Yo(x), med index I i intervallet från 0 till n-1. Formeln för att upprätta Lagrange -polynomer är som följer:

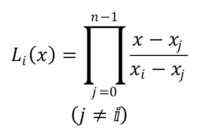
Den visade symbolen indikerar att produktoriet av n -1 monomialer måste utföras, från polynomet j = 0.

Egenskaper hos Lagrange -polynomer

1.- Lagrange -polynomer är exakt samma som enheten när de utvärderas i abscissa som motsvarar deras index, det vill säga:

L_Yo(x_Yo) = 1

2.- De avbryts i abscissen av interpoleringspunkterna med index som skiljer sig från samma polynom:

Kan tjäna dig: Beskrivande statistik: Historia, egenskaper, exempel, begrepp

L_Yo(x_J) = 0, med i ≠ j.

3.- Genom att ta andra Abscissa -värden som skiljer sig från interpoleringspunkter, förvärvar Lagrange Polynomials värden mellan -1 och +1.

4.- För att få Lagrange -polynomer är det bara nödvändigt att veta abscissen för punkterna till Interpoch.

Andra grader Lagrange -polynomer

Second -graden Lagrange Polynomials är de som används oftast när du vill göra en trepunktsinterpolation.

Anta att den interpolära funktionen är känd i tre punkter, som är:

(x₀,och₀); (x₁, och₁); (x₂, och₂)

Sedan dina motsvarande Lagrange -polynomer L₀, L₁ och L₂ De blir så här:

L₀(x) = [(x - x₁) / (X₀ - x₁)] [(x - x₂) / (X₀ - x₂)]]

L₁(x) = [(x - x₀) / (X₁ - x₀)] [(x - x₂) / (X₁ - x₂)]]

L₂(x) = [(x - x₀) / (X₂ - x₀)] [(x - x₁) / (X₂ - x₁)]]

Det bör nämnas att L₀(x₀) = L₁(x₁) = L₂(x₂) = 1, medan L_Yo(x_J) = 0 så länge som Yo≠ j.

Interpolationspolynom i andra graden

Det är viktigt att notera att i Lagranges interpoleringspolynom är ordinaterna av interpoleringspunkter Lagrange -polynomfaktorer.

På detta sätt, när polynomerna har erhållits för vissa värden på abscissen, tjänar de till att beräkna interpoleringspolynomet för olika funktioner, förutsatt att den beställda i den tidigare fasta abscissen är känd.

När det gäller en interpolation av andra klass:

P (x) = f (x₀) L₀(x) + f (x₁) L₁(x) + f (x₂) L₂(x)

Och p (x) närmar sig funktionen f (x) i intervallet (x₀, x₂).

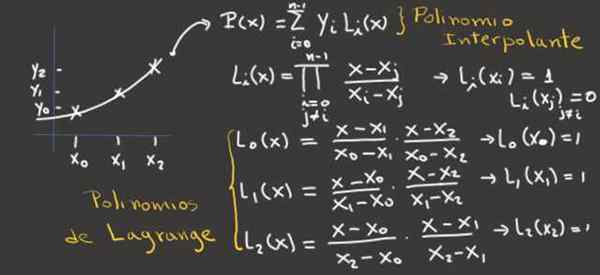figur 2.- Denna bild visar hur man får Lagrange -polynomerna för tre interpoleringspunkter och från dem, det interpolerande polynomet. Källa: f. Zapata.

Exempel

Exempel 1

Hitta Lagrange -polynomerna som motsvarar tre abscissa -punkter x₀= 0, x₁= 1 och x₂= 2.

Som framgår av föregående avsnitt kommer dessa polynomer att vara:

Kan tjäna dig: överjektiv funktion: definition, egenskaper, exempel

L₀(x) = [(x - 1) / (0 - 1)] [(x - 2) / (0 - 2)] = - (x -1) ⋅ (-½) (x - 2) = ½ ( x² - 3x + 2)

L₁(x) = [(x - 0) / (1 - 0)] [(x - 2) / (1 - 2)] = x ⋅ (-1) (x - 2) = - x² + 2x

L₂(x) = [(x - 0) / (2 - 0)] [(x - 1) / (2 - 1)] = (½) x ⋅ (x - 1) = (½) (x² - x)

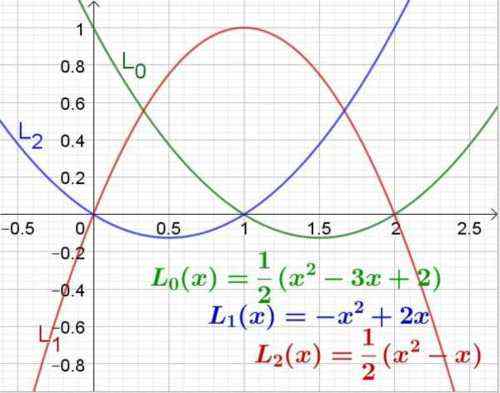Figur 3. Lagrange -polynom för Abscissa -värden 0, 1 och 2. Källa: f. Zapata.

Exempel 2

Du vill ungefärliga funktionen f (x) = arcan (x) I intervallet [0, 2]. Av denna funktion är bara deras värden kända för x₀= 0, x₁= 1 och x₂= 2, som är respektive och₀= 0, och₁= π/4 = 0,785 och och₂= 1,107.

Därför måste du hitta det interpolerande polynomet P (x) närmar sig f (x) I det angivna intervallet.

I exempel 1 har Lagrange -polynomer redan fastställts för de abscissa -värden som anges i detta uttalande, så det är inte nödvändigt att upprepa beräkningen. Interpoling Polynomial kommer nu att vara:

P (x) = f (x₀) L₀(x) + f (x₁) L₁(x) + f (x₂) L₂(x)

Vilket motsvarar:

P (x) = y₀ L₀(x) + och₁ L₁(x) + och₂ L₂(x)

I detta specifika fall är det:

P (x) = 0 ∙ (½) (x² - 3x + 2) + 0,785 ∙ (- x² + 2x) + 1 107 ∙ (½) (x² - x)

Ovanstående förenklas för:

P (x) = 0,785 ∙ (- x² + 2x) + 1 107 ∙ (½) (x² - x)

Och slutligen återstår:

P (x) = -0,2315 ∙ x² + 1 0165 ∙ x

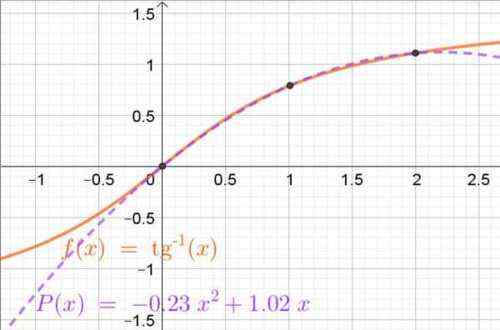Figur 4. Interpoleringspolynom erhållet genom LaGrange-polynomer som approximerar Arc-tangent-funktionen i intervallet (0, 2). Interpoleringspunkter visas också. Källa: f. Zapata.

Övningar

Övning 1

Få adekvata Lagrange -polynom för att ha en strategi för funktionen:

f (x) = sin (x)

I intervallet [0, π] och med fem interpoleringspunkter.

Lösning

För det första bestäms abscissen av interpoleringspunkterna, som väljs lika och inklusive ändarna på tillnärmningsintervallet. Med detta har du:

x₀= 0; x₁= π/4; x₂= π/2; x₃= 3 π/4; x₄= π.

Kan tjäna dig: ojämlikheten i triangeln: demonstration, exempel, lösta övningar

Eftersom f (x) avbryts vid extrema punkter kommer det inte att vara nödvändigt att få Lagrange l -polynomerna l₀ och jag₄.

Polynomer l₁, L₂ och jag₃ är:

L₁ = [(x - x₀) / (X₁ - x₀)] [(x - x₂) / (X₁ - x₂)] [(x - x₃) / (X₁ - x₃)] [(x - x₄) / (X₁ - x₄)]]

L₂ = [(x - x₀) / (X₂ - x₀)] [(x - x₁) / (X₂ - x₁)] [(x - x₃) / (X₂ - x₃)] [(x - x₄) / (X₂ - x₄)]]

L₃ = [(x - x₀) / (X₃ - x₀)] [(x - x₁) / (X₃ - x₁)] [(x - x₂) / (X₃ - x₂)] [(x - x₄) / (X₃ - x₄)]]

Nu ersätter vi värdet på abscissen:

L₁ = [(x - 0)/(π/4 - 0)] [(x - π/2)/(π/4 - π/2)] [(x - 3 π/4)/(π/4 - 3 π/4)] [(x - π)/(π/4 - π)]

L₂ = [(x - 0)/(π/2 - 0)] [(x - π/4)/(π/2 - π/4)] [(x - 3 π/4)/(π/2 - 3 π/4)] [(x - π)/(π/2 - π)]

L₃ = [(x - 0)/(3 π/4 - 0)] [(x - π/4)/(3 π/4 - π/4)] [(x - π/2)/(3 π/ 4 - π/2)] [(x - π)/(3 π/4 - π)]

Nämnare löses:

L₁ = [x/π/4] [(x - π/2)/( - π/4)] [(x - 3 π/4)/( - π/2)] [(x - π)/( - 3π/4)]

L₂ = [x/π/2] [(x - π/4)/(π/4)] [(x - 3 π/4)/( - π/4)] [(x - π)/( - π /2)]

L₃ = [x/(3 π/4)] [(x - π/4)/(π/2)] [(x - π/2)/(π/4)] [(x - π)/( - π/4)]

Det förenklas och omgrupperas för att få:

L₁ = x (x - π/2) (x - 3 π/4) (x - π)/( - 3 π ⁴/128)

L₂ = x (x - π/4) (x - 3 π/4) (x - π)/(π ⁴/64)

L₃ = x (x - π/4) (x - π/2) (x - π)/( - 3 π ⁴/128)

Övning 2

Skaffa interpolationspolynomet som närmar sig SEN (x) -funktionen i intervallet [0, π] med de fem interpoleringspunkter som valts i övning 1 och deras respektive lagrange -polynomier.

Lösning

Interpolationspolynomet är:

P (x) = sin (0) * l₀ + Sen (π/4) * l₁ + Sen (π/2) * l₂ + Sen (3π/4) * l₃ + Sen (π) * l4

Att utvärdera sinus- och multiplikationsfunktionen är:

P (x) = (√2/2) l₁ + 1 * L₂ + (-I/2) l₃

Efter ett svårt algebraiskt arbete är interpoleringspolynom:

P (x) = 2. 7481 x⁴ -femton. 138 x³ +23. 467 x² - 9. 5236 x

Referenser

1. Goodman, a. L. H. nitton nittiosex. Algebra och trigonometri med analytisk geometri. Pearson Education.
2. Harpe, s. d. (2000). Ämnen i geometrisk gruppteori. University of Chicago Press.
3. Hazewinkel, m. (2001). Linjär interpolering ", Encyclopedia of Mathematics.
4. Hoffmann, E. (2002). Till kronologi av interpolering: från forntida astronomi till modern signal och bildbehandling. IEEE: s förfarande.
5. Wikipedia. Lagrange polynominterpolation. Återhämtat sig från: Wikipedia.com