Hooke lagformler, exempel, applikationer, övningar

De Hookes lag påpekar att deformationen som ett elastiskt objekt upplever är direkt proportionell mot den applicerade kraften på den. Proportionalitetskonstanten beror på objektets natur, dess geometri och materialet som det tillverkas.

Allt material har elastiska egenskaper i större eller mindre utsträckning, så de följer Hookes lag när de återgår till sina ursprungliga dimensioner, när styrkan upphör att. Elastiska fjädrar och tandkött är bra exempel på föremål som följer Hookes lag, men det är också stålcabillerna som ingår i en bro.

Figur 1. Hookes lag på våren

Att ta som ett exempel på en vår eller brygga, för att hålla den sträckt eller komprimerad är det nödvändigt att tillämpa en kraft vars storlek är f. Enligt Hookes lag kommer våren att uppleva en x -deformation:

F ∝ x

Proportionalitetskonstanten, som, som är en fjäder, kallas vårstyvhet, Det betecknas därför K: därför:

F = k⋅x

I enheterna i det internationella systemet kommer kraften i Newton (n) och deformationen i meter (m). Därför har vårkonstanten N/M -enheter. Vårkonstanten representerar kraften som måste appliceras för att deformera den i 1 m i längd.

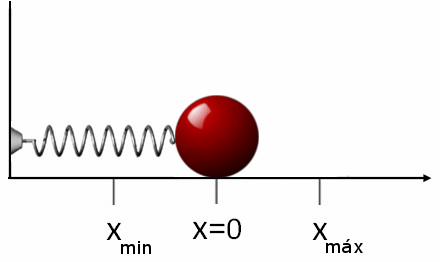figur 2. När fjädern är sträckt är kraften som utövas på objektet motsatt. Detsamma händer om våren krymper, i det här fallet driver det föremålet i motsatt mening. Källa: Wikimedia Commons.

Om den efter sträckning eller komprimering av våren släpps kommer den att röra sig i motsatt riktning till den applicerade kraften. Detta betyder att om vi sträcker det är det komprimerat och vice versa. Det är därför Force F_R den där Vårövningarna är:

F_R = -k⋅x

Det negativa tecknet indikerar vad som sägs: att styrkan motsätter sig förskjutning, så denna kraft är känd som Återställande styrka.

[TOC]

Formel och ekvationer

Förhållandet mellan kraft och förskjutning i en vår upptäcktes av Robert Hooke (1635-1703), en anmärkningsvärd engelsk fysiker och känd för sin rivalitet med Isaac Newton. Hooke var en mångsidig forskare som framgångsrikt dabbade inom olika vetenskapsområden: mekanik, biologi, astronomi och arkitektur.

Figur 3. Den engelska fysikern Robert Hooke, som inte känner till porträtt av tiden. Detta är en återuppbyggnad gjord av konstnären Rita Gerer 2004 genom beskrivningar som lämnats av dem som träffade forskaren. Källa: Wikimedia Commons. Rita Greer / Fal.

Hooke insåg att om kraften som appliceras på en pir inte är så stor, är bryggan proportionellt deformeras för att tvinga, och när den en gång nämnda kraften försvinner har våren sin naturliga längd igen.

Kan tjäna dig: Jordens magnetosfär: Egenskaper, struktur, gaser

På detta sätt har Hookes lag grafiskt formen av en rak linje, vars lutning är vårkonstanten. Följande bild visar kraften som utövas på våren för att sträcka den - eller komprimera den - beroende på X -positionen. Observera att kraften inte beror på vårens naturliga längd, utan på dess förskjutning.

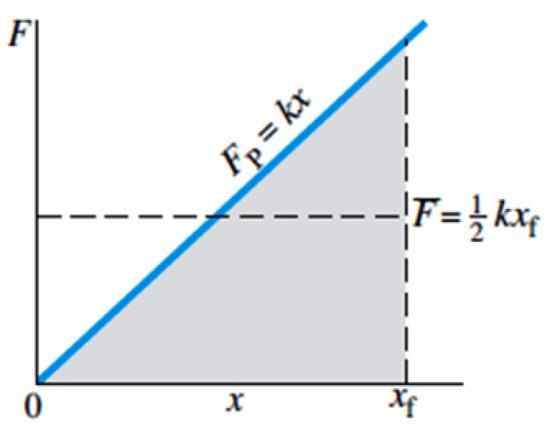Figur 4. Storlek f av den nödvändiga kraften för att sträcka eller komprimera en fjäder, beroende på x -deformationen. Källa: Giancoli, D. Fysik med applikationer.

Medelkraften indikeras i grafen av F med stången och motsvarar ½ kx_F, där x_F är vårens slutliga position.

Både kraften som utövas på våren, och den kraft han utövar på ett föremål som är bundet till honom, är varierande krafter. Ju mer du vill sträcka eller komprimera till våren, desto mer styrka måste du använda för att kunna uppnå det.

Arbete som görs för att sträcka eller komprimera en vår

När en kraft appliceras som deformerar våren, är ett verk som lagras på våren och som kan användas senare.

Mekaniskt arbete definieras som området under grafen för kraft F beroende på position x. För att beräkna arbetet med en variabel kraft f (x) gör när du flyttar ett objekt från position x₁ att positionera x₂ Den definierade integralen måste beräknas:

När det gäller det arbete som krävs för att få en fjäder från sin jämviktsposition till position x_F Det är väldigt enkelt, eftersom det område som ska beräknas är det av den grå skuggade triangeln i figur 4, vars formel är känd:

Triangelområdet = ½ bas. höjd

Därför är det nödvändiga arbetet:

W = ½ x_F . (KX_F) = ½ k (x_F)²

Och om du vill beräkna det nödvändiga arbetet för att ta till våren från position x till position x_F, Det skulle motsvara beräkningen av det repade trapesområdet i figur 5:

W = ½ k (x_F)² - ½ k x²

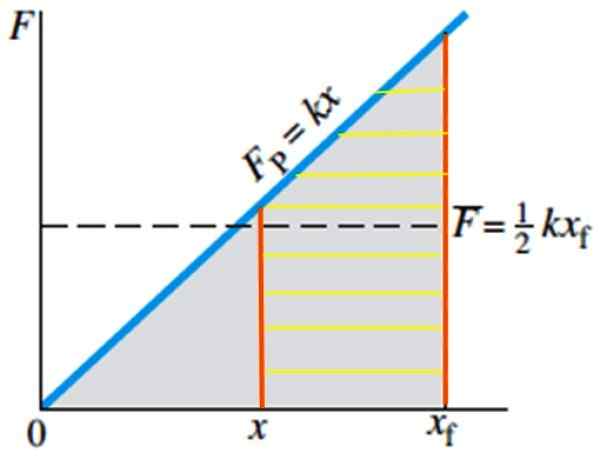Figur 5. Arbetet som gjorts för att sträcka våren från position X till XF -position motsvarande Rayada -området. Källa: Giancoli, D. Fysik med applikationer.

Exempel på fjädrar

Enligt applikationen som de är avsedda kan fjädrarna vara cylindriska, koniska, spiral, med ett cirkulärt tvärsnitt (det vanligaste), av fyrkantig eller rektangulär sektion.

Kan tjäna dig: elektriska ledare

En allmänt använt klassificering är enligt vilken typ av ansträngning de kommer att underkastas: det finns torsion, flexion, komprimering och förlängningsfjädrar. De senare används i stor utsträckning och det fungerar också för spänning och komprimering.

Tryckfjäder

Ett exempel på kompressionsfjäder är vad som används i leksaken som heter Pogo antingen Salto palo. Dessa fjädrar lagrar en ganska potentiell energi när de komprimeras och släpps gradvis medan de återvänder till jämviktspositionen. På detta sätt är returerna inte alltför plötsliga.

Figur 6. Pogo eller Saltoín Stick är baserad på en kompressionsfjäder. Källa: Wikimedia Commons.

Förlängning och torsionsfjädrar

Våren för spramp är typen av förlängningsfjädrar och tillverkas med väl rullade varv, med två krokar i ändarna. De kan behålla tillräckligt med potentiell energi, som de senare släpper när någon stiger och börjar hoppa på duken, som också har sitt eget elastiska svar, som alla material.

Torsionsfjädrar är mycket vanliga, eftersom de tjänar till att göra klädklämmor. I stället för krokar i ändarna, böjer de sig i vinkeln, för att motstå de krafter som tenderar att utöva torsion.

Figur 7. Fjädrarna är en del av otaliga mekanismer, till exempel dessa klädpincett. Källa: PXFuel.

Material för tillverkningsfjädrar

De mest lämpliga materialen för att göra fjädrar är de med en Ultimat motstånd (slutlig motstånd), det vill säga de stöder en stor ansträngning innan de bryter. Det är också bekvämt att materialet har en hög kryppunkt, så att det inte förlorar sina elastiska egenskaper med små ansträngningar.

Industriella fjädrar tillverkas med legeringar som inkluderar stål med högt kol, koppar, nickel och bronsinnehåll.

Hookes lagansökningar

Eftersom fjädrarna har dygden att lagra potentiell energi när de sträcker sig eller komprimerar, kan de göra arbete genom att flytta saker som mekanismer.

På detta sätt har fjädrarna många applikationer, från små och dagliga föremål, genom bilar, till maskiner av alla slag. Fjädrarna tjänar till:

-Chockvibrationer.

-Tillverkar infällbara mekanismer: penna, hängande pincett, hårkrokar.

-Gör våren eller dynamometrar

Och de är också en del av mekanismen för:

Kan tjäna dig: stängd elektrisk krets

-Klockor.

-Trampoliner.

-Lås.

-Leksaker.

-Vapen.

-Nålmätare, till exempel galvanometern, används för att mäta strömmar, spänningar och motstånd.

Löst övningar

- Övning 1

En storlek av storlek 5 tillämpas.0 n på en vår, vilket gör en längd på 3 sträcka.5 cm från sin naturliga längd.

a) Hur mycket sträcks när den applicerade kraften är 7 n?

b) Hitta det arbete som gjorts av den applicerade styrkan för att sträcka till våren 3.5 cm från sin naturliga längd.

Lösning till

Att veta att våren är sträcka 3.5 cm genom tillämpningen av 5.0 n Vi kan beräkna din konstant:

k = f / x = 5.0 n / 3.5 cm = 1.43 N / cm.

När en 7 N -kraft appliceras erhålls följande sträcka:

x = f / k = 7.0 n / 1.43 N/m = 4.9 cm

Lösning B

Det nödvändiga arbetet för att deformera en fjäder ges av:

W = ½ kx² = 0.5 x 1.43 N / CM X (3.5 cm)² = 8.76 n . cm = 8.76 n . 1 x10 ^-2 m = 0.0876 J.

- Övning 2

En vår av föraktlig deg och 10 cm lång hänger från ett stöd. Om en massa på 2 kg hängas, sträcks våren tills den når 15 cm. Beräkna:

a) Vårkonstanten

b) fjäderstorleken när en massa på 3 kg är suspenderad.

Lösning till

Vårsträckan är x = 15 - 10 cm = 5 cm

Eftersom systemet är i statisk jämvikt, riktas kraften som utövas av våren när sträckningen riktas vertikalt uppåt, för att kompensera för vikt, som riktas ner, då: sedan:

F_R = W → kx = mg

K = 2 x 9.8 n / 5 x10 ^-2 M = 392 N/M

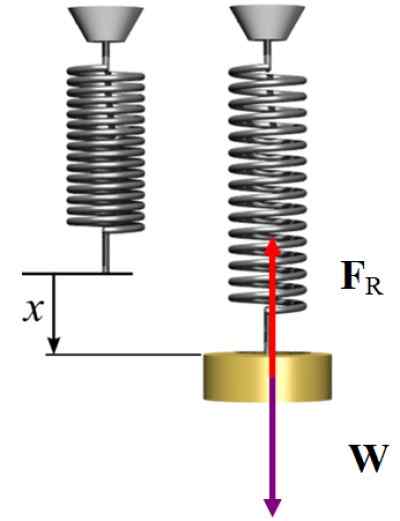Gratis kroppsdiagram för övningen löstes 2. Källa: Wikimedia Commons/F. Zapata.

Lösning B

När en vikt på 3 kg är suspenderad är den nya kraften W = 3 x 9.8 n = 29.4 n

I det här fallet är sträckan:

x = mg /k = 29. 4 N / 392 N / M = 0.075 m = 7.5 cm

Referenser

1. Bauer, w. 2011. Fysik för teknik och vetenskap. Volym 1. MC Graw Hill.
2. Kreativa mekanismer blogg. Fyra olika typer av fjädrar. Återställt från: CreativeMechanisms.com.
3. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Volym 2. Dynamisk. Redigerad av Douglas Figueroa (USB).
4. Giancoli, D.  2006. Fysik: Principer med applikationer. Sjätte. Ed. Prentice hall.
5. Riddare, r.  2017. Fysik för forskare och teknik: En strategistrategi.  Pearson.