Klasvarumärke

Vad är ett klassmärke?

De Klasvarumärke, Även känd som mittpunkten är det värdet som är i mitten av en klass, som representerar alla värden som finns i den kategorin. I grund och botten används klassmärket för beräkning av vissa parametrar, såsom aritmetiskt medelvärde eller standardavvikelse.

Då är klassmärket mittpunkten för alla intervall. Detta värde är också mycket användbart för att hitta variansen i en datauppsättning som redan är grupperad i CLAS.

Frekvensfördelning

För att förstå vad ett klassmärke är nödvändigt begreppet frekvensfördelning. Med tanke på en datauppsättning är en frekvensfördelning en tabell som delar upp dessa data i ett antal kategorier som kallas klasser.

Denna tabell visar vad som är mängden element som tillhör varje klass; Det senare är känt som frekvens.

I den här tabellen offras en del av den information vi får från uppgifterna, eftersom vi istället för att ha det individuella värdet på varje element, vi vet bara att den tillhör denna klass.

Å andra sidan får vi bättre förståelse för datauppsättningen, eftersom det på detta sätt är lättare att uppskatta etablerade mönster, vilket underlättar manipulationen av nämnda data.

Hur många klasser överväger?

För att göra en frekvensfördelning måste vi först bestämma antalet klasser som du vill ta och välja klassgränserna för samma.

Kan tjäna dig: kanter på en kub

Valet av hur många klasser som tar bör vara bekvämt, med hänsyn till att ett litet antal klasser kan dölja information om de data vi vill studera och en mycket stor kan generera för många detaljer som inte nödvändigtvis är användbara.

De faktorer som vi måste ta hänsyn till när vi väljer hur många klasser som är flera, men mellan dessa är två: den första är att ta hänsyn till hur många data vi måste tänka på; Den andra är att veta vilken storlek distributionsområdet är (det vill säga skillnaden mellan den största och minsta observationen).

Efter att ha haft de redan definierade klasserna fortsätter vi att räkna hur många data i varje klass. Detta nummer kallas klassfrekvens och betecknas per fix.

Som vi tidigare har sagt har vi en frekvensfördelning förlorar informationen som kommer individuellt från varje data eller observation. Därför söks ett värde som representerar hela klassen som den tillhör; Detta värde är klassmärket.

Hur erhålls det?

Klassmärket är det centrala värdet som representerar en klass. Det erhålls genom att lägga till gränserna för intervallet och dela detta värde med två. Vi kunde uttrycka detta matematiskt på följande sätt:

x_Yo= (Nedre gränsen + övre gräns)/2.

I detta uttryck x_Yo Betecknar varumärket för I-This Class.

Exempel

Med tanke på följande datauppsättning, ge en representativ frekvensfördelning och få motsvarande klassmärke.

Eftersom data med det högsta numeriska värdet är 391 och barnet är 221, har vi att intervallet är 391 -221 = 170.

Kan tjäna dig: Teoretisk sannolikhet: Hur man får ut det, exempel, övningar

Vi väljer 5 klasser, alla med samma storlek. Ett sätt att välja klasser är som följer:

Observera att varje data är i en klass, dessa är disjunkt och har samma värde. Ett annat sätt att välja klasser är att överväga data som en del av en kontinuerlig variabel, som kan nå något verkligt värde. I det här fallet kan vi överväga klasser av formuläret:

205-245, 245-285, 285-325, 325-365, 365-405

Detta sätt att gruppera uppgifterna kan dock presentera vissa oklarheter med gränserna. Till exempel i fallet med 245 uppstår frågan: vilken klass tillhör den, till den första eller den andra?

För att undvika denna förvirring görs en konvention av extrema punkter. På detta sätt kommer den första klassen att vara intervallet (205 245], den andra (245 285], och så vidare.

När klasserna har definierats fortsätter vi att beräkna frekvensen och vi har följande tabell:

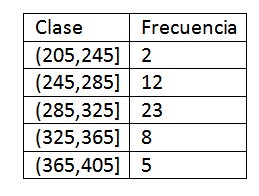
Efter att ha fått frekvensfördelningen av data fortsätter vi att hitta klassmärkena för varje intervall. Vi måste verkligen:

x₁= (205+ 245)/2 = 225

x₂= (245+ 285)/2 = 265          

x₃= (285+ 325)/2 = 305

x₄= (325+ 365)/2 = 345

x₅= (365+ 405)/2 = 385

Vi kan representera detta genom följande graf:

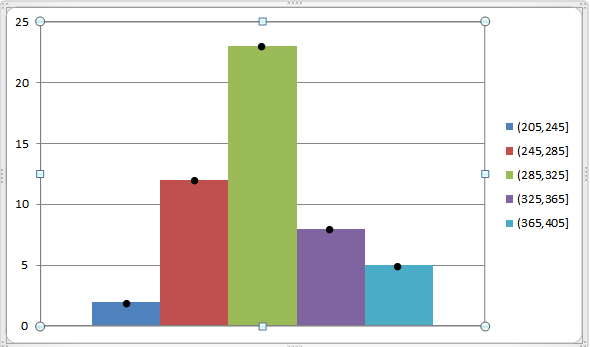
Vad är det för?

Klassmärket är mycket funktionellt för att hitta det aritmetiska medelvärdet och variansen i en datargrupp som redan har grupperats i olika klasser.

Vi kan definiera det aritmetiska medelvärdet som summan av observationerna som erhållits mellan provstorleken. Ur fysisk synvinkel är dess tolkning som balanspunkten för en datauppsättning.

Att identifiera en hel uppsättning data med ett enda nummer kan vara riskabelt, så du måste också ta hänsyn till skillnaden mellan denna jämviktspunkt och de verkliga data. Dessa värden är kända som avvikelse från det aritmetiska medelvärdet, och med dessa försöker det bestämma hur mycket aritmetiskt medelvärde av data varierar.

Kan tjäna dig: fraktioner: typer, exempel, övningar löst

Det vanligaste sättet att hitta detta värde är på grund av variansen, som är genomsnittet av kvadrarna i avvikelserna i det aritmetiska medelvärdet.

För att beräkna det aritmetiska medelvärdet och variationen i en uppsättning data grupperade i en klass använder vi följande formler, respektive:

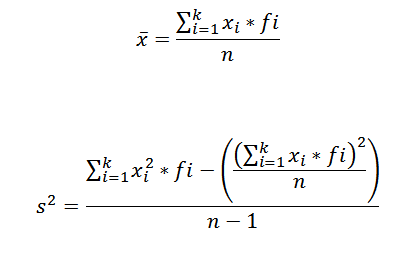
I dessa uttryck x_Yo  Det är i-detta klassmärke, f_Yo representerar motsvarande frekvens och K antalet klasser där data grupperades.

Exempel

Genom att använda de data som anges i föregående exempel måste vi utöka lite mer data i frekvensfördelningstabellen. Följande erhålls:

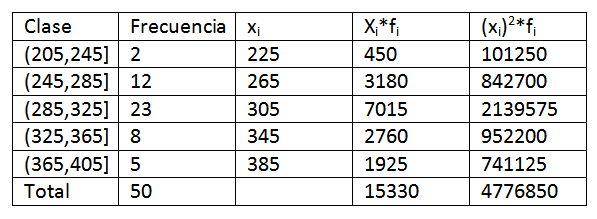
Sedan, genom att ersätta data i formeln, har vi lämnat att det aritmetiska medelvärdet är:

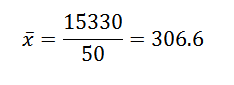
Dess varians och standardavvikelse är:

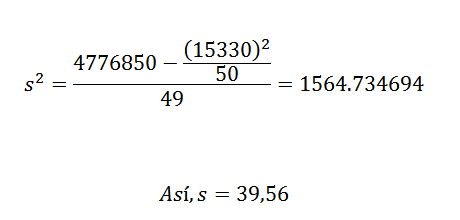
Från detta kan vi dra slutsatsen att de ursprungliga uppgifterna har ett aritmetiskt medelvärde på 306,6 och en standardavvikelse på 39,56.