Heltal

Vad är hela nummer?

Hela siffror utgör en uppsättning användbara siffror för att räkna de kompletta objekten som har haft och de som inte är. Också för att räkna dem på ena sidan och den andra av en viss referensplats.

Även med hela siffrorna kan subtraktionen eller skillnaden genomföras mellan ett antal och en annan större än honom, till exempel som en skuld. Skillnaden mellan vinster och skulder görs med tecken + respektive -.

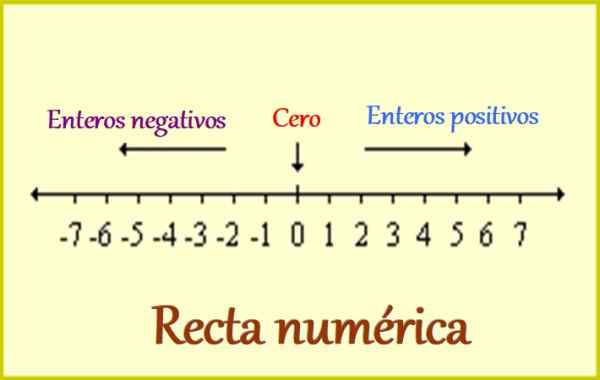
Figur 1. Den numeriska linjen för hela siffror. Källa: Wikimedia Commons. Leomg/cc by-sa (https: // creativecommons.Org/licenser/BY-SA/3.0).

Det är därför hela siffrorna innehåller följande:

-Positiva heltal, som är skrivna föregås av ett +-tecken, eller helt enkelt utan skylten, eftersom det också förstås att de är positiva. Till exempel: +1, +2, +3 ... och så vidare.

-0, där tecknet är irrelevant, eftersom det inte lägger till det för att subtrahera det från någon mängd. Men 0 är mycket viktigt, eftersom det är referensen för heltal: På ena sidan finns de positiva och de negativa, som vi ser i den övre figuren.

-Negativa heltal, som alltid måste skrivas från skylten -eftersom med dem de belopp som skulder och alla de som finns på andra sidan referensen skiljer sig. Exempel på negativa heltal är: -1, -2, -3 ... och sedan dess.

Hur är hela siffrorna?

I början representerar vi hela siffrorna med inställningen av uppsättningen: z = ... -4, -3, -2, -1, 0, +1, +2, +3, +4 ..., det vill säga listad och organiserad. Men en mycket användbar representation är det som använder den numeriska linjen. För detta är det nödvändigt att rita en linje, som vanligtvis är horisontell, på vilken 0 är markerad och uppdelad i identiska avsnitt:

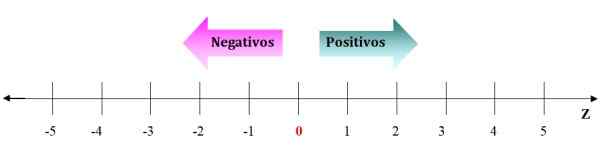figur 2. Representation av hela siffror på den numeriska linjen. Från 0 till höger är de positiva heltalen och från 0 till vänster negativer. Källa: f. Zapata.

Negativen går till vänster om 0 och de positiva går till höger. Pilarna på sifferlinjen symboliserar att siffrorna fortsätter till oändligheten. Med tanke på alla heltal är det alltid möjligt att hitta ett som är större eller annat än är lägre.

Det absoluta värdet på ett heltal

Det absoluta värdet på ett heltal är avståndet mellan antalet och 0. Och avstånd är alltid positiva. Därför är det absoluta värdet på det negativa heltalet numret utan dess tecken mindre.

Till exempel är det absoluta värdet på -5 5. Det absoluta värdet betecknas med staplar enligt följande:

| -5 | = 5

För att visualisera det räcker det att ha utrymmen på den numeriska linjen, från -5 till 0. Medan det absoluta värdet på ett positivt heltal är samma nummer, till exempel | +3 | = 3, eftersom dess avstånd till 0 är 3 mellanslag:

Kan tjäna dig: Sandwich Law: Förklaring och övningar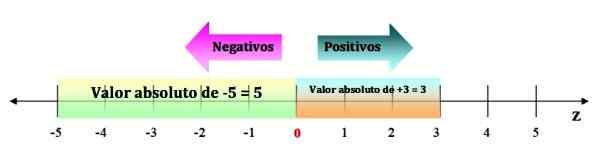Figur 3. Det absoluta värdet på ett heltal är alltid ett positivt belopp. Källa: f. Zapata.

Egenskaper

-Uppsättningen av hela siffror betecknas som z och inkluderar uppsättningen naturliga siffror n, deras element är oändliga.

-Ett heltalsnummer och det som följer (eller den som föregår det) skiljer sig alltid i enheten. Till exempel efter 5 kommer 6, att vara 1 skillnaden mellan dem.

-Varje helt nummer har en föregångare och en efterträdare.

-Något positivt heltal är större än 0.

-Ett negativt heltal är alltid mindre än 0 och att något positivt antal. Låt oss till exempel ta numret -100, detta är mindre än 2, än 10 och 50. Men det är också mindre än -10, -20 och -99 och det är större än -200.

-0 har inga teckenhänsyn, eftersom det inte är negativt eller positivt.

-Med hela siffrorna kan samma operationer som utförs med de naturliga siffrorna utföras, nämligen: summa, subtraktion, multiplikation, potentiering och mer.

-Hela motsatsen till ett visst heltal x, är -x och summan av ett heltal med dess motsats är 0:

x + (-x) = 0.

Operationer med hela siffror

- Tillägg

-Om siffrorna som ska läggas till har samma tecken läggs deras absoluta värden och resultatet placeras på tecknet på att tillägget har. Här är några exempel:

a) (+8) +( +9) = 8 +9 = +17

b) (-12) + ( - 10) = - (12 + 10) = -22

-I händelse av att siffrorna har olika tecken subtraheras de absoluta värdena (majoren av den minderåriga) och resultatet placeras tecknet på antalet med det högsta absoluta värdet, enligt följande:

a) (-8) + (21) = 21 - 8 = 13

b) (-9) + (+4) = -(9-4) = -5

Egenskaper för summan av hela siffror

-Summan är kommutativ, därför ändrar inte tilläggsordningen summan. Låt A och B vara två hela siffror, det uppfylls att A+B = B+A

-0 är det neutrala elementet i summan av hela siffror: a + 0 = a

-Alla helt nummer som läggs till med dess motsats är 0. Motsatsen till + a är -a, och omvänt, motsatsen till -a es + a. Därför: (+ a)+ (-a) = 0.

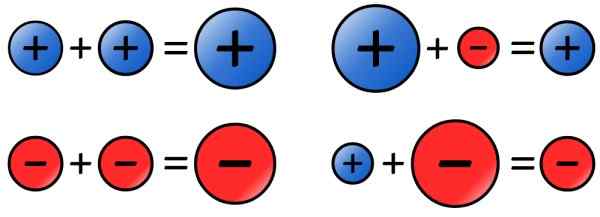Figur 4. Tecken regel för summan av hela siffror. Källa: Wikimedia Commons.

- Subtraktion

För att subtrahera hela siffror måste du vägledas av denna regel: Subtraktionen motsvarar summan av ett nummer med dess motsats. Låt två siffror A och B, då:

A - B = A + (-B)

Anta till exempel att du måste göra följande operation: (-3) - (+7), sedan:

(-3) -(+7) = (-3)+( -7) = -(3+7) = -10

- Multiplikation

Multiplikationen av hela siffror följer vissa regler för skyltarna:

-Produkten av två nummer med Samma tecken Det är alltid positivt.

-När två siffror multipliceras olika tecken, Resultatet är alltid negativt.

Kan tjäna dig: vad är delarna av fraktionen? (Exempel)

-Produktens värde är lika med att multiplicera respektive absoluta värden.

Omedelbart några exempel som klargör ovanstående:

(-5) x (+8) = -5 x 8 = -40

(-10) x (-12) = 10 x 12 = 120

(+4) x (+32) = 4 x 32 = 128

Egenskaper för multiplikation av hela siffror

-Multiplikation är kommutativ. Vara två hela siffror a och b, det är sant att: a.b = b.A, som också kan uttryckas som:

Faktorernas ordning förändrar inte produkten.

-Det neutrala elementet i multiplikation är 1. Vara till ett heltal, därför till.1 = 1

-Alla heltal multiplicerat med 0 är lika med 0: a.0 = 0

Fördelningsfastigheter

Multiplikation möter fördelningsegenskapen med avseende på summan. Ja A, B och C är hela siffrorna då:

till.(b +c) = a.b + a.c

Sedan ett exempel på hur man tillämpar den här egenskapen:

(-3). [(-4) + 11] = (-3).(-4)+(-3).11 = 12 -33 = 12 + (-33) = -21

Förstärkning

-Om basen är positiv är resultatet av operationen alltid positivt.

-När basen är negativ, om exponenten är jämn, är resultatet positivt. Och om exponenten är udda är resultatet negativt.

- Division

I divisionen gäller samma regler för tecken som i multiplikation:

-Genom att dela två heltal av samma tecken är resultatet alltid positivt.

-När två heltal med olika tecken är uppdelade är kvoten negativ.

Till exempel:

(-12) ÷ (-4) = 3

33 ÷ (-3) = -11

Viktig: Divisionen är inte kommutativ, med andra ord till ÷ b ≠ b ÷ a och som alltid är uppdelningen mellan 0 inte tillåtet.

- Förstärkning

Vara ett helt antal och vi vill höja det till en exponent n, då måste vi multiplicera av sig själv, som visas nedan:

tillⁿ = a.till.till.till.Till ... till

Låt oss också överväga följande, med hänsyn till att N är ett naturligt antal:

-Om A är negativt och N är jämnt är resultatet positivt.

-När A är negativt och N är udda resulterar det i ett negativt antal.

-Om A är positiv och N är jämn eller udda, är det alltid ett positivt heltal.

-Alla heltal som är förhöjda till 0 är lika med 1: a⁰ = 1

-Varje nummer högt till 1 är lika med antalet: a¹ = a

Låt oss till exempel säga att du vill hitta (-3)⁴ , För att göra det multiplicerar (-3) fyra gånger av sig själv, så här: (-3).(-3).(-3).(-3) = 81.

Ett annat exempel, även med ett negativt heltal är:

(-2)³ = (-2).(-2).(-2) = -8

Produkt av lika baskrafter

Anta att två krafter med lika bas, om vi multiplicerar dem får vi en annan kraft med samma bas, vars exponent är summan av de givna exponenterna:

tillⁿ ·till^m = a^{n + m}

Lika baspulverförhållande

Genom att dela krafter i samma bas är resultatet en kraft med samma bas, vars exponent är subtraktionen av de givna exponenterna:

Kan tjäna dig: Vinklar i omkretsen: typer, egenskaper, lösta övningar

tillⁿ ÷ a^m = a^{n - m}

Sedan två exempel som klargör dessa punkter:

(-2)³.(-2)⁵ = (-2) ³⁺⁵= (-2)⁸

5⁶ ÷ 5⁴ = 5^6-4 = 5²

Exempel

Låt oss titta på enkla exempel för att tillämpa dessa regler och komma ihåg att tecknet kan komma ihåg att tecknet kan fördelas med:

a) (+6) + (+14) = 6 + 14 = 20

b) (-8) + ( - 10) = - (8 + 10) = -18

c) (-16) + (+7) = -16 + 7 = -9

d) (+4) + (-8) + (-25) = [(+4) + (-8)] + (-25) = [4-8] -25 = -4 -25 = -29

e) (-8) -( + 15) = (-8) + (-15) = -8 -15 = -23

f) (+3) x (+9) = 3 x 9 = 27

g) (- 4) x (-11) = 4 x 11 = 44

h) (+5) x (-12) = -5 x 12 = -60

i) (-2)³ = (-2) x (-2) x (-2) = -8

Löst övningar

- Övning 1

En myra rör sig på sifferraden i figur 1. Från punkt x = +3 utför följande förskjutningar:

-7 enheter rör sig till höger

-Nu returneras 5 enheter till vänster

-Gå 3 enheter till vänster.

-Den returnerar och flyttar 4 enheter till höger.

Vid vilken tidpunkt är myran i slutet av rutten?

Lösning

Låt oss ringa förskjutningarna. När de är till höger får de ett positivt tecken och när de är på vänster negativa tecken. På detta sätt och börjar från x = +3 har du:

-Första D: x₁ = +3 +7 = +10

-Andra D: x₂ = +10 +(-5) = +5

-Tredje d: x₃ = +5 +(-3) = +2

-Fjärde d: x₄ = +2 +4 = +6

När myran slutar är promenaden i läget x = +6. Det vill säga det är 6 enheter till höger om 0 på den numeriska linjen.

- Övning 2

Lös följande operation:

36 + [- (-4 + (-5)- 7)].-[-6+5- (2+7-9)]+2 (-8+6)]

Lösning

Denna operation innehåller tecken på gruppering, som är parentes, fyrkantiga parenteser och nycklar. När du löser måste du ta hand om parenteserna först efter fyrkantiga parenteser och slutligen nycklarna. Med andra ord måste du arbeta inifrån och ut.

I denna övning representerar punkten en multiplikation, men i fallet mellan ett nummer och en parentes eller annan symbol finns det ingen mening, på samma sätt som det förstås att det är en produkt.

Därefter, upplösningen steg för steg, färgerna fungerar som en guide för att följa resultatet av minskningen av parentes, som är de mest interna gruppsymbolerna:

36 + [- (-4 + (-5)- 7)].-[-6+5- (2+7-9)]+2 (-8+6)] =

= 36 + [- (-16)].-[-6+ 5- (0)]+ 2 (-2)] =

= 36 + [16].-[-1] -4] =

= 52.1- 4] = 52.-3 = -156

- Övning 3

Lös den första gradsekvationen:

12 + x = 30 + 3x

Lösning

Villkoren är grupperade med det okända till vänster om jämlikhet och de numeriska termerna till höger:

x - 3x = 30 - 12

- 2x = 18

X = 18 / (-2)

x = - 9