TACHTENBERG METOD Vad är, exempel

han Trachtenberg -metoden Det är ett system att utföra aritmetiska operationer, främst multiplikation, på ett enkelt och snabbt sätt, när deras regler har varit kända och dominerade.

Han utformades av den ryska ingenjören Jakow Trachtenberg (1888-1953) när han var en fånge i nazisterna i ett koncentrationsläger, som en form av distraktion för att upprätthålla förnuft medan han fortsatte i fångenskap.

Figur 1. Multiplikationstabeller. Källa: Wikimedia Commons. Taulacat [CC BY-SA 3.0 (https: // CreativeCommons.Org/licenser/BY-SA/3.0)] [TOC]

Vad är fördelar och nackdelar

Fördelen som denna metod representerar är att för att utföra multiplikationer är det inte nödvändigt.

Nackdelen är att det inte finns någon universell regel att multiplicera med någon siffra, men regeln varierar beroende på multiplikatorn. Mönster är emellertid inte svåra att memorera och i princip tillåter operationer utan papper och penna.

Under hela denna artikel kommer vi att koncentrera oss på reglerna för att snabbt multiplicera.

[TOC]

Exempel

För att tillämpa metoden är det nödvändigt att känna till reglerna, så vi kommer att presentera dem en efter en och med exempel:

- Multiplicera en siffra med 10 eller 11

Multiplikationsregel med 10

-För att multiplicera alla siffror med 10 läggs en noll helt enkelt till höger. Till exempel: 52 x 10 = 520.

Regler för att multiplicera med 11

-En noll läggs till i början och i slutet av figuren.

-Varje siffra läggs till med sin högra granne och resultatet placeras under motsvarande siffra för den ursprungliga figuren.

-Om resultatet överstiger nio, noteras enheten och en liten punkt placeras för att komma ihåg att vi bär en enhet som kommer att läggas till i summan av nästa figur med sin högra granne.

Detaljerat multiplikationsexempel med 11

Multiplicera 673179 av 11

Kan tjäna dig: konvergensradio: definition, exempel och övningar löst

06731790 x 11 =

--

= 7404969

De nödvändiga stegen för att nå detta resultat, illustrerade genom färger, är följande:

-1 i multiplikatorenheten (11) multiplicerades med multiplikatorn 9 (06731790) och den lades till 0. Enhetssiffran erhölls: 9.

-Sedan multiplicerar det 1 till 7 och lägger till nio ger 16 och vi har 1, dussin siffran placeras: 6.

-Sedan multiplicerar 1 med 1 tillagd grannen till höger 7 plus 1 som ledde som ett resultat 9 För hundra.

-Nästa siffra erhålls från att multiplicera 1 till 3 plus angränsande 1, det resultat 4 För siffran med tusentals.

-Det är multiplicerat 1 av 7 och grannen läggs till resulterande 10, noll placeras (0) som tionde siffran och det tar en.

-Då är 1 för 6 plus granne 7 13 plus en 1 som var 14, 4 som en siffra på hundratusentals och tar 1.

-Slutligen multiplicera 1 med noll som lades till i början, vilket gav noll mer grannen 6 plus en som tog. Det är äntligen 7 För siffran som motsvarar miljoner.

- Multiplikation med siffror från 12 till 19

För att multiplicera med 12 alla siffror: 

-En noll läggs till i början och ytterligare en noll i slutet av figuren för att multiplicera.

-Varje siffra fördubblas från figuren som ska multipliceras och lägger till med sin högra granne.

-Om summan överstiger 10 en enhet läggs till i nästa dupliceringsoperation och lägger till med grannen.

Exempel på multiplikation med 12

Multiplicera 63247 med 12

0632470 x 12 =

-

758964

Detaljerna för att nå detta resultat, strikt efter de regler som anges, visas i följande figur:

figur 2. Trachtenberg -metoden för att multiplicera valfritt antal med 12. Källa: f. Zapata.

- Förlängning av reglerna för multiplikationer med 13, ... fram till 19

Metoden för multiplikation med 12 kan utvidgas till multiplikationer med 13, 14 till 19 helt enkelt ändra dupliceringsregeln för de tretton, fyrdubbla i fallet med 14 och så vidare tills det når 19.

Kan tjäna dig: ortogonal matris: egenskaper, demonstration, exempel

Regler för produkter med 6, 7 och 5

- Multiplikation med 6

-Lägg till nollor i början och slutet av figuren som ska multipliceras med 6.

-Lägg till hälften av sin höger till höger till varje siffra, men om siffran är konstigt att lägga till 5 dessutom.

Figur 3. Multiplikation av en figur med 6, efter Trachtenberg -metoden. Källa: f. Zapata.

- Multiplikation med 7

-Lägg till nollor till början och i slutet av figuren för att multiplicera.

-Duplicera varje siffra och lägg till den nedre hela halvan av grannen, men om siffran tillsättes 5.

Exempel på multiplikation med 7

-Multiplicera 3412 med 7

-Resultatet är 23884. För att tillämpa reglerna rekommenderas först att känna igen de udda siffrorna och placera en liten 5 för att komma ihåg att du lägger till denna siffra till resultatet.

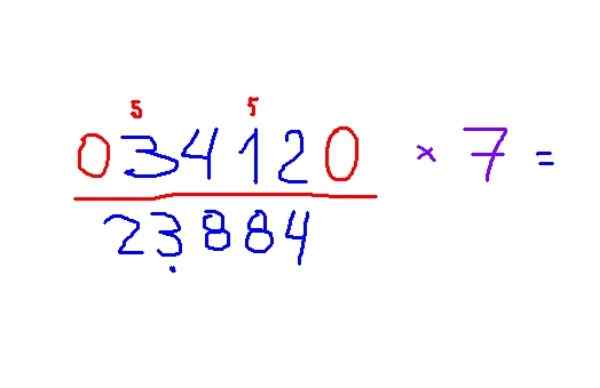Figur 4. Exempel Multiplikation av en figur med 7, enligt Trachtenbergs metod. Källa: f. Zapata.

- Multiplikation med 5

-Lägg till nollor till början och i slutet av figuren för att multiplicera.

-Placera under varje siffra den nedre halvan av grannen till höger, men om siffran är udda dessutom 5.

Exempel multiplikation med 5

Multiplicera 256413 med 5

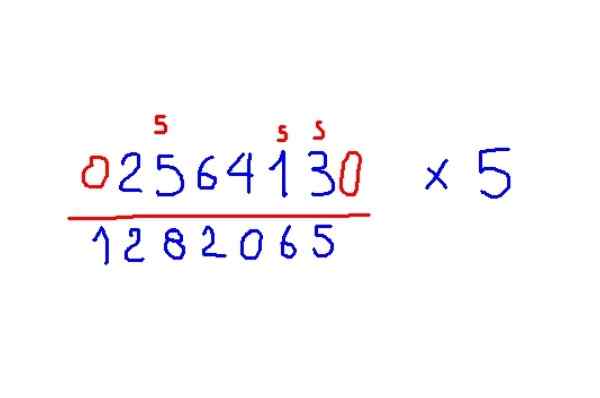Figur 5. Exempel Multiplikation av en figur med 5, enligt Trachtenberg -metoden. Källa: f. Zapata.

Regler för produkter av 9

-En noll läggs till i början och en annan i slutet av figuren för att multiplicera med nio.

-Den första siffran till höger erhålls från att subtrahera motsvarande siffra för figuren för att multiplicera.

-Sedan subtraheras nästa siffra och grannen läggs till.

-Det föregående steget upprepas tills du når noll av multipliceringen, där vi subtraherar 1 från grannen och resultatet kopieras under noll.

Kan tjäna dig: vad är delarna av 30? (Förklaring)

Exempel på multiplikation med 9

Multiplicera 8769 med 9:

087690 x 9 =

--

78921

Operationer

10 - 9 = 1

(9-6) + 9 = 12 (De 2 Och det tar 1)

(9-7)+1+6 =9

(9-8) +7 =8

(8-1) = 7

Multiplikation med 8, 4, 3 och 2

-Lägg till nollor till början och i slutet av figuren för att multiplicera.

-För den första siffran till höger subtrahera från 10 och resultatet fördubblas.

-För följande siffror subtraherar från 9 fördubblas resultatet och grannen läggs till.

-När du når noll subtrahera 2 från höger till höger.

- Multiplikation med 8

Exempel på multiplikation med 8

-Multiplicera 789 med 8

Figur 6. Exempel Multiplikation av en figur med 8, enligt Trachtenberg -metoden. Källa: f. Zapata.

- Multiplikation med 4

-Lägg till nollor till höger och vänster om multiplicering.

-Subtrahera från 10 motsvarande siffra för enheten och lägga till 5 om det är en udda siffra.

-Subtrahera från 9 i form av varje multiplikerande siffra, lägga till halva grannen till höger och om det är en udda siffra att lägga till 5 dessutom.

-Efter att ha nått noll i början av multipliceringsplatsen hälften av grannen utom en.

Exempel på multiplikation med 4

Multiplicera 365187 x 4

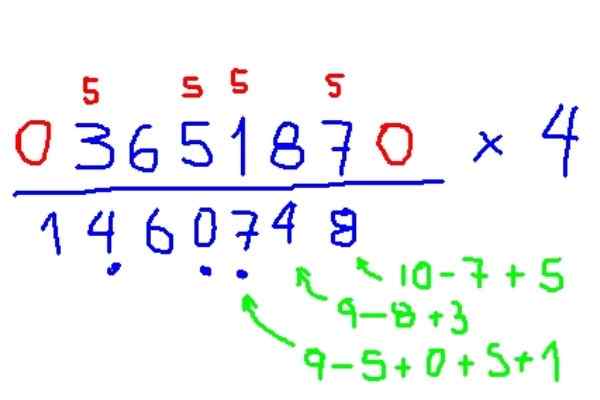Figur 7. Exempel Multiplikation av en figur med 4, enligt Trachtenberg -metoden. Källa: f. Zapata.

- Multiplikation med 3

-Lägg till noll i varje ände av multiplicering.

-Subtrahera 10 utom enhetens siffra och lägg till 5 om det är en udda siffra.

-För de andra siffrorna, subtrahera 9 duplicera resultatet, lägg till hälften av grannen och lägg till 5 om det är udda.

-När du når noll på rubriken, placera hela halvan av grannen minus 2.

Exempel på multiplikation med 3

Multiplicera 2588 med 3

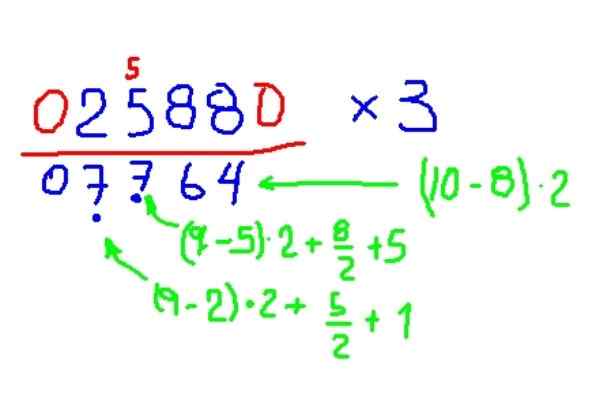Figur 8. Exempel Multiplikation av en figur med 3, enligt Trachtenberg -metoden. Källa: f. Zapata.

- Multiplikation med 2

-Lägg till nollor i ändarna och dubbel varje siffra, om du överstiger 10 lägg till en till nästa.

Exempel multiplikation med 2

Multiplicera 2374 med 2

023740 x 2

04748

Multiplicera med sammansatta figurer

Reglerna som anges ovan tillämpas, men resultaten körs till vänster antalet platser som motsvarar tiotals, hundratals och så vidare. Låt oss titta på följande exempel:

Träning 

Multiplicera 37654 av 498

0376540 x 498

301232 Regel för 8

338886 Regel för 9

150616 regel för 4

18751692 Sista summa

Referenser

1. Cutler, Ann. 1960.Trachtenberg -hastighetssystemet för grundläggande matematik. Doubleday & Co, NY.
2. Dialnät. Snabb grundläggande matematiksystem. Återhämtat sig från: dialnet.com
3. Matematisk hörn. Snabb multiplikation med Trachtenbergs metod. Återhämtad från: rinconmathematical.com
4. Trachtenberg -hastighetssystemet för grundläggande matematik. Återhämtat sig från: Trachtenbergspeedmath.com
5. Wikipedia. Trachtenberg -metoden. Återhämtat sig från: Wikipedia.com