Reynolds nummer vad är det för, hur det beräknas, övningar

han Reynolds nummer (R_och) Det är en dimensionell numerisk mängd som fastställer förhållandet mellan tröghetskrafterna och de viskösa krafterna hos en rörelsevätska. Tröghetsstyrkor bestäms av Newtons andra lag och ansvarar för den maximala vätskedaccelerationen. De viskösa krafterna är de krafter som motsätter sig vätskans rörelse.

Reynolds -numret appliceras på alla typer av vätskeflöde såsom flöde i cirkulära eller icke -cirkulära kanaler, i öppna kanaler och flödet runt nedsänkta kroppar.

Värdet på Reynolds -antalet beror på densitet, viskositet, vätskehastighet och dimensionerna på den aktuella rutten. Beteendet hos en vätska beroende på mängden energi som sprids, på grund av friktion beror det på om flödet är laminärt, turbulent eller mellanliggande. Av denna anledning är det nödvändigt att hitta ett sätt att bestämma vilken typ av flöde.

Ett sätt att bestämma det är genom experimentella metoder men kräver mycket precision i mätningar. Ett annat sätt att bestämma vilken typ av flöde är genom att få Reynolds -numret.

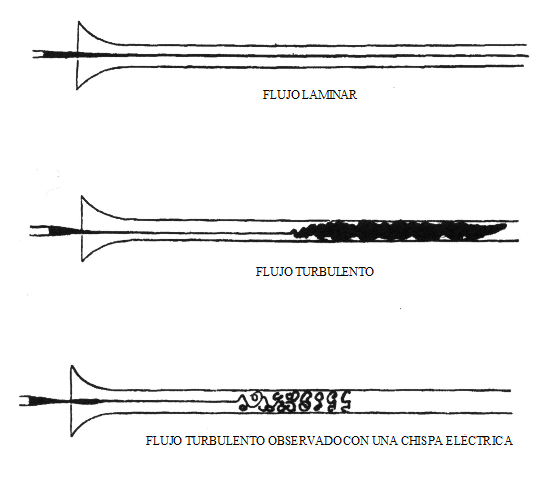
Vattenflöde observerat av Osborne Reynolds [av Osborne Reynolds (https: // commons.Wikimedia.org/wiki/fil: reynolds_observations_urbulence_1883.Svg)]

1883 upptäckte Osborne Reynolds att om värdet på detta dimensionella antal är känt, kan den typ av flöde som kännetecknar alla fluidledningssituationer förutsägas.

[TOC]

Vad är Reynolds -numret för?

Reynolds nummer tjänar till att bestämma en vätska, det vill säga för att bestämma om flödet av en vätska är laminärt eller turbulent. Flödet är laminärt när de viskösa krafterna, som motsätter sig vätskans rörelse, är de som dominerar och vätskan rör sig med tillräckligt liten hastighet och i rektilinär bana.

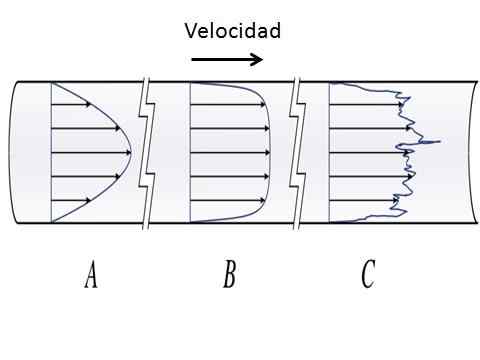Hastigheten på en vätska som rör sig genom en cirkulär kanal, för laminärt flöde (A) och turbulent flöde (B och C). [Av Olivier Cleynen (https: // commons.Wikimedia.org/wiki/fil: pipe_flow_velocity_distribusion_laminar_turbulent.Svg)]

Vätskan med laminärt flöde uppför sig som om de var oändliga lager som glider över de andra, på ett ordnat sätt, utan att blanda. I cirkulära kanaler har laminärt flöde en parabolisk hastighetsprofil, med maximala värden i mitten av kanalen och minimivärden i skikten nära kanalytan. Värdet på Reynolds -antalet i laminärt flöde är R_och<2000.

Flödet är turbulent när tröghetskrafterna är dominerande och vätskan rör sig med fluktuerande förändringar av oregelbunden hastighet och banor. Det turbulenta flödet är mycket instabilt och har överföringar av rörelse mellan vätskepartiklarna.

Kan tjäna dig: kalciumfluorid (CAF2): struktur, egenskaper, användningar

När vätskan cirkulerar i en cirkulär kanal, med turbulent flöde, korsar vätskeskikten med varandra och bildar virvlar och deras rörelse tenderar att vara kaotisk. Värdet på Reynolds -numret för ett turbulent flöde i en cirkulär kanal är R_och > 4000.

Övergången mellan det laminära flödet och det turbulenta flödet sker för värden på Reynolds -numret mellan 2000 och 4000.

Hur beräknas det?

Ekvationen som används för att beräkna Reynolds -numret i en cirkulär tvärsnittskanal är:

R_och = ρvd/η

ρ = Vätsketäthet (kg/m³)

V = Flödeshastighet (m³/s)

D = Linjär dimension Karakteristiska vätskesor som i fallet med cirkulär kanal representerar diametern.

η = dynamisk viskositet hos vätskan (Pa.s)

Förhållandet mellan viskositet och densitet definieras som kinematisk viskositet v = η/ρ, Och din enhet är m²/s.

Ekvationen för Reynolds -antalet beroende på den kinematiska viskositeten är:

R_och = Vd/v

I kanaler och kanaler med icke -cirkulära tvärsnitt är den karakteristiska dimensionen känd som hydraulisk diameter D_H och representerar en generaliserad dimension av fluidvägen.

Den generaliserade ekvationen för att beräkna Reynolds -numret i kanaler med icke -cirkulära tvärsnitt är:

R_och = ρv 'd_H /η

V '= Genomsnittlig flödeshastighet =Går

Den hydrauliska diametern D_H upprättar förhållandet mellan området TILL av tvärsnittet av flödesströmmen och den våta omkretsen P_M .

D_H = 4a/p_M

Den våta omkretsen P_M Det är summan av längderna på kanalens väggar, eller kanalen, som är i kontakt med vätskan.

Du kan också beräkna Reynolds -numret på en vätska som omger ett objekt. Till exempel en sfär nedsänkt i en vätska genom att röra sig med hastighet V. Sfären upplever en dragkraft F_R definieras av Stokes -ekvationen.

F_R = 6πrvη

R = sfärradio

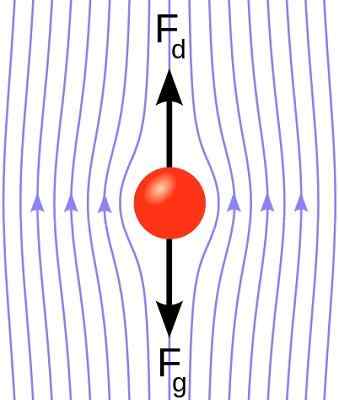Sfärhastighetsprofil nedsänkt i en vätska. Dragkraften motsätter sig tyngdkraften. [Av Kraaiennest (https: // commons.Wikimedia.org/wiki/fil: stokes_sphere.Svg)]

Reynolds antal av en sfär med hastighet V nedsänkt i en vätska är:

R_och = ρv r /η

R_och<1 cuando el flujo es laminar y R_och > 1 när flödet är turbulent.

Löst övningar

Nedan följer tre applikationsövningar av Reynolds -numret: cirkulär kanal, rektangulär kanal och sfär nedsänkt i en vätska.

Det kan tjäna dig: skärning av skärning: Hur beräknas och löses

Reynolds nummer i en cirkulär kanal

Beräkna Reynolds antal propylenglykol till 20 °C i en cirkulär diameter kanal 0,5 cm. Flödeshastighetens storlek är 0,15 m³/s. Vad är typen av flöde?

D =0,5 cm = 5.10^-3m (Karakteristisk dimension)

Vätsketäthet är ρ = 1 036 g/cm³= 1036 kg/ m³

Vätskeviskositet är η = 0,042 Pa · s = 0,042 kg/m.s

Flödeshastighet är V = 0,15 m³/s

Reynolds -nummerekvationen används i en cirkulär kanal.

R_och =ρDU/η

R_och = (1036 kg/ m³X0,15 m³/s x 5.10^-3m)/(0,042 kg/m.s) = 18,5

Flödet är laminärt eftersom värdet på Reynolds -antalet är lågt med avseende på förhållandet R_och<2000

Reynolds nummer i en rektangulär kanal

Bestäm vilken typ av etanolflöde som flyter med 25 ml/min hastighet i ett rektangulärt rör. Måtten på den rektangulära sektionen är 0,5 cm och 0,8 cm.

Densitet ρ = 789 kg/m³

Dynamisk viskositet η = 1 074 MPa · s = 1,074.10^-3 kg/m.s

Först bestäms den genomsnittliga flödeshastigheten.

V ' =Går

V = 25 ml/min = 4,16.10^-7m³/s

Tvärsnittet är rektangulärt vars sidor är 0,005 m och 0,008 m. Tvärsektionsområdet är A = 0,005 m x0,008 m = 4.10^-5m²

V ' = (4.16.10^-7m³/s) /(4.10^-5m²) = 1,04 × 10^-2Fröken

Den våta omkretsen är summan av rektangelns sidor.

P_M=0,013 m

Den hydrauliska diametern är D_H = 4a/p_M

D_H = 4 × 4.10^-5m²/0.013m

D_H= 1.23.10^-2m

Reynolds nummer erhålls från ekvationen R_och = ρv 'd_H /η

R_och = (789 kg/m³X1.04 × 10^-2m/s x1.23.10^-2m)/ 1 074.10^-3 kg/m.s

R_och = 93974

Flödet är turbulent eftersom Reynolds nummer är mycket stort (R_och> 2000)

Reynolds antal sfärer nedsänkt i en vätska

En sfärisk partikel, från polystiren latex, vars radie är R= 2000nm Det kastas vertikalt i vattnet med en initial storlekshastighet V₀= 10 m/s. Bestäm Reynolds -numret för partikeln nedsänkt i vattnet

Partikeldensitet  ρ = 1,04 g/cm³ = 1040 kg/m³

R= 2000nm = 0,000002m

Vattentäthet ρ_Ag= 1000 kg/m³ 

Gegga η =0,001 kg/(m · s)

Reynolds nummer erhålls genom ekvation R_och = ρv r /η

R_och = (1000 kg/m³x10 m/s x 0,000002m)/ 0,001 kg/(m · s)

R_och = 20

Reynolds nummer är 20. Flödet är turbulent.

Ansökningar

Reynolds nummer spelar en viktig roll i vätskemekanik och termisk överföring eftersom det är en av de viktigaste parametrarna som kännetecknar en vätska. Några av dina ansökningar nämns nedan.

Det kan tjäna dig: stationära vågor: formler, egenskaper, typer, exempel

1-det används för att simulera rörelsen av organismer som rör sig på flytande ytor som: Bakterier hängande i vatten som simmar genom vätska och producerar slumpmässig omröring.

2-It har praktiska tillämpningar i flödet av rör och i flytande cirkulationskanaler, begränsade flöden, särskilt i porösa medier.

3-i suspensionerna av fasta partiklar nedsänkta i en vätska och emulsioner.

4-Reynolds-numret tillämpas på vindtunneltesterna för att studera de aerodynamiska egenskaperna hos flera ytor, särskilt när det gäller flygplanflyg.

5-it används för att modellera insektrörelse i luften.

6-den kemiska reaktordesignen kräver att man använder Reynolds-numret för att välja flödesmodell enligt belastningsförluster, energiförbrukning och värmeöverföringsområdet.

7-i förutsägelsen av värmeöverföring av elektroniska komponenter (1).

8-i den bevattnade processen i trädgårdarna och fruktträdgårdar där vattenflödet som kommer ut ur rören behövs. För att få denna information bestäms förlusten av hydraulisk belastning som är relaterad till den friktion som finns mellan rörets vatten och väggarna. Förlust av last beräknas när Reynolds -numret har erhållits.

Vindtunnel [av Juan Kulichevsky (https: // Commons.Wikimedia.org/wiki/fil: t%c3%banel_de_viento_ (35351654140).Jpg)]

Biologiapplikationer 

I biologi kräver studien av rörelse av levande organismer genom vatten eller i vätskor med vattenliknande egenskaper att få Reynolds -antalet, vilket kommer att bero på storleken på organismerna och den hastighet som de rör sig.

Unicellulära bakterier och organismer har ett mycket lågt Reynolds -nummer (R_och<<1), följaktligen har flödet en laminär hastighetsprofil med en övervägande av viskösa krafter.

Organismer nära myror (upp till 1 cm) har ett Reynolds -nummer i storleksordningen 1, vilket motsvarar övergångsregimen i vilken tröghetskrafterna som verkar på kroppen är lika viktiga eftersom viskens viskösa krafter.

I större organismer som People Reynolds nummer är mycket stort (R_och>> 1).

Referenser

1. Tillämpning av lågreynolds nummer turbulenta flödesmodeller för förutsägelse av elektronisk komponentvärmeöverföring. Rodgers, P och Eveloy, V. Nv: s.n., 2004, IEEE, Vol. 1, s. 495-503.
2. Mott, r l. Applicerad vätskemekanik. Berkeley, CA: Pearson Prentice Hall, 2006, Vol. Yo.
3. Collieu, a m och powney, d j. Materialets mekaniska och themala egenskaper. New York: Crane Russsak, 1973.
4. Kay, J M och Nedderman, R M. En introduktion till vätskemekanik och värmeöverföring. New York: Cambridge University Press, 1974.
5. Happel, J och Brenner, h. Mekanik för vätskor och transportprocess. Hingham, MA: Martinuss Nijhoff Publishers, 1983.