Komplexa sifferegenskaper, exempel, operationer

De komplexa tal De är den numeriska uppsättningen som täcker de verkliga siffrorna och alla polynomens rötter, inklusive de jämna rötterna till de negativa siffrorna. Dessa rötter finns inte i uppsättningen av verkliga siffror, men i komplexa siffror är lösningen.

Ett komplext antal består av en verklig del och en annan som kallas "imaginär". Den verkliga delen kallas till, Till exempel och den imaginära delen Ib, med till och b verkliga siffror och "jag" gillar Imaginär enhet. På detta sätt tar det komplexa numret formuläret:

Z = a + ib

Figur 1.- Binomial representation av ett komplext antal när det gäller verklig del och imaginär del. Källa: Pixabay.

Exempel på komplexa siffror är 2 - 3i, -πi, 1 + (1/2) i. Men innan vi arbetar med dem, låt oss se var den imaginära enheten härstammar från Yo, Med tanke på denna kvadratiska ekvation:

x² - 10x + 34 = 0

Där a = 1, b = -10 och c = 34.

När lösningsmedelsformeln appliceras för att bestämma lösningen hittar vi följande:

Hur man bestämmer värdet på √-36? Det finns inget riktigt antal att kvadrat är ett negativt belopp. Då dras slutsatsen att denna ekvation inte har några riktiga lösningar.

Vi kan dock skriva detta:

√-36 = √-6² = √6² (-1) = 6√-1

Om vi ​​definierar ett visst värde x Så att:

x² = -1

Så:

x = ± √-1

Och den tidigare ekvationen skulle ha en lösning. Därför definierades den imaginära enheten som:

I = √-1

Och så:

√-36 = 6i

Många antikvitetsmatematiker arbetade med att lösa liknande problem och lyfte fram Renaissance Girolamo Cardano (1501-1576), Nicolo Fontana (1501-1557) och Raffaele Bombelli (1526-1572).

År senare René Descartes (1596-1650) kallade "imaginära" till mängder som √-36 i exemplet. Av denna anledning är √-1 känd som Imaginär enhet.

[TOC]

Komplexa sifferegenskaper

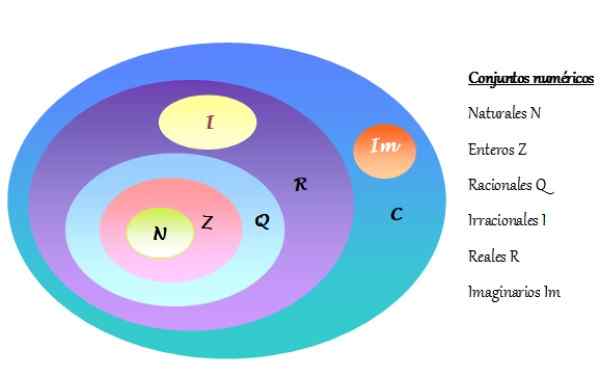
-Uppsättningen av komplexa siffror betecknas som C och inkluderar verkliga siffror r och imaginära siffror im. Numeriska uppsättningar representeras i ett Venn -diagram, som visas i följande figur:

Kan tjäna dig: Löst faktoriseringsövningar figur 2. Venn -diagram över numeriska uppsättningar. Källa: f. Zapata.

-Varje komplext antal består av en verklig del och en annan imaginär del.

-När den imaginära delen av ett komplext nummer är 0 är det ett rent verkligt antal.

-Om den verkliga delen av ett komplext nummer är 0, är ​​antalet rent imaginärt.

-Två komplexa siffror är desamma om deras respektive verkliga del och imaginär del är desamma.

-Med de komplexa siffrorna genomförs de kända operationerna av summor, subtraktion, multiplikation, produkt och empowerment, vilket resulterar i ett annat komplext nummer.

Representation av komplexa siffror

Komplexa siffror kan representeras på olika sätt. Här är de viktigaste:

- Binomform

Det är den givna formen i början, där z är det komplexa numret, till är den verkliga delen, b är den imaginära delen och Yo Det är den imaginära enheten:

Z = a + ib

Eller också:

Z = x + iy

Ett sätt att grafera det komplexa numret är genom det komplexa planet som visas i denna figur. Den imaginära axeln är vertikal, medan den verkliga axeln är horisontell och betecknar som re.

Det komplexa antalet z Det representeras i detta plan som en koordinatpunkt (X, y) antingen (A, B), Som görs med punkterna i det verkliga planet.

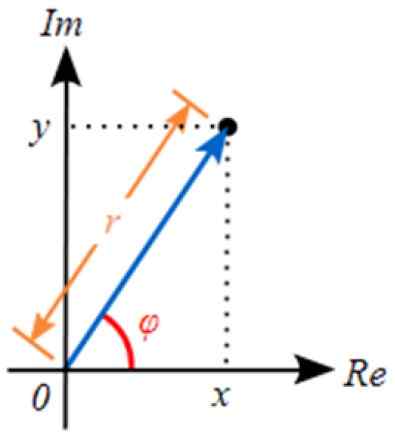
Avståndet från ursprung till punkt Z är modulen för det komplexa antalet, betecknat som r, Medan φ är vinkeln som bildas r Med den riktiga axeln.

Figur 3. Representation av ett komplext antal i det komplexa planet. Källa: Wikimedia Commons.

Denna representation är nära besläktad med vektorerna i det verkliga planet. Värdet på R motsvarar modul av det komplexa antalet.

Det kan tjäna dig: Gauss-Seidel Method: Förklaring, applikationer, exempel

- Polär form

Den polära formen består i att uttrycka det komplexa antalet som ger värdena r och av φ. Om vi ​​tittar på figuren, värdet av r Det motsvarar hypotenusen av en höger triangel. Kategorierna är värda till och b, Nåväl x och och.

I binomial- eller binomialformen kan vi gå vidare till den polära formen genom:

R = √x²+och²

Vinkeln φ Det är den som bildar R -segmentet med den horisontella axeln eller imaginär axel. Det är känt som argument av det komplexa antalet. Den här vägen:

φ = arctg (y/x)

Argumentet har oändliga värden, med hänsyn till att varje gång en retur vänds, vilket är värt 2π -radianer, har R igen samma position. På detta sätt uttrycks i allmänhet argumentet från Z, betecknad arg (z), enligt följande:

Arg (z) = φ + 2kπ

Där k är hel och tjänar till att ange mängden svängar vänd: 2, 3, 4 .. . Tecknet indikerar betydelsen av rotationen, om tid eller antihorario görs.

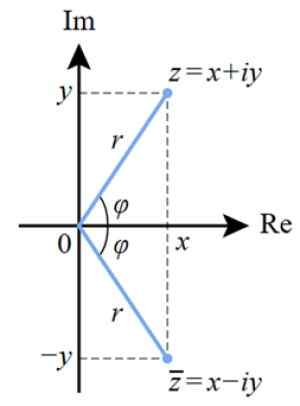
Figur 4. Polär representation av ett komplext antal i det komplexa planet. Källa: Wikimedia Commons.

Och om vi vill överföra den polära formen till binomialformen, använder vi trigonometriska skäl. Från föregående siffra kan vi se det:

x = r cos φ

y = r sen φ

På detta sätt z = r (cos φ+i sin φ)

Det är förkortat så här:

z = r cis φ

Exempel på komplexa nummer

Följande komplexa siffror ges binomiellt:

a) 3 + i

b) 4

d) -6i

Och dessa i ett ordnat vridmoment:

a) (-5, -3)

b) (0, 9)

c) (7.0)

Slutligen ges denna grupp polär eller trigonometrisk:

a) √2 cis 45º

b) √3 cis 30º

Kan tjäna dig: hypergeometrisk distribution: formler, ekvationer, modell

c) 2 cis 315º

Vad är de för?

Användbarheten av komplexa siffror går utöver upplösningen av den andra gradsekvationen som visas i början, eftersom de är väsentliga inom området teknik och fysik, särskilt i:

-Studien av elektromagnetiska vågor

-Alternativ ström- och spänningsanalys

-Modelleringen av alla slags signaler

-Relativitetsteori, där tiden antas som en imaginär storlek.

Operationer med komplexa siffror

Med de komplexa siffrorna kan vi utföra alla operationer som görs med det verkliga. Vissa är lättare att göra om siffrorna kommer binomiskt, till exempel sum och subtraktion. Å andra sidan är multiplikation och uppdelning enklare om de utförs med den polära formen.

Låt oss titta på några exempel:

- Exempel 1

Lägg till z₁ = 2 + 5i och z₂ = -3 -8i

Lösning

De verkliga delarna läggs till separat från de imaginära delarna:

z₁ + z₂ = (2 + 5i) + (-3 -8i) = -1 -3i

- Exempel 2

Multiplicera z₁ = 4 cis 45º och z₂ = 5 cis 120º

Lösning

Det kan demonstreras att produkten av två komplexa siffror i polär eller trigonometrisk ges av:

z₁ . z₂ = r₁.r₂ Cis (φ₁ + φ₂)

Enligt det här:

z₁ . z₂ = (4 × 5) cis (45 + 120) = 20 cis 165º

Ansökan

En enkel tillämpning av komplexa siffror är att hitta alla rötter till en polynomekvation som den som visas i början av artikeln.

När det gäller ekvation x² - 10x + 34 = 0, vid applicering av lösningsmedelsformeln erhålls det:

Därför är lösningarna:

x₁ = 5 + 3i

x₂ = 5 - 3i

Referenser

1. Earl, r. Komplexa tal. Återhämtat sig från: matematik.oxe.Växelström.Storbritannien.
2. Figuera, J. 2000. Matematik 1: a. Diversifierad. Co-bo-utgåvor.
3. Hoffmann, J. 2005. Urval av matematikfrågor. Monfort Publications.
4. Jiménez, r. 2008. Algebra. Prentice hall.
5. Wikipedia. Komplexa tal. Hämtad från: i.Wikipedia.org