Imaginära siffror egenskaper, applikationer, exempel

De Imaginära siffror De är de som ger lösning på ekvationen där den okända, kvadrathöjda, är lika med ett verkligt negativt antal. Den imaginära enheten är I = √ (-1).

I ekvationen: z²= - a, z Det är ett imaginärt antal som uttrycks enligt följande:

 Z = √ (-a) = i√ (a)

Varelse till Ett positivt verkligt antal. Ja A = 1, så z = i, var Yo är den imaginära enheten.

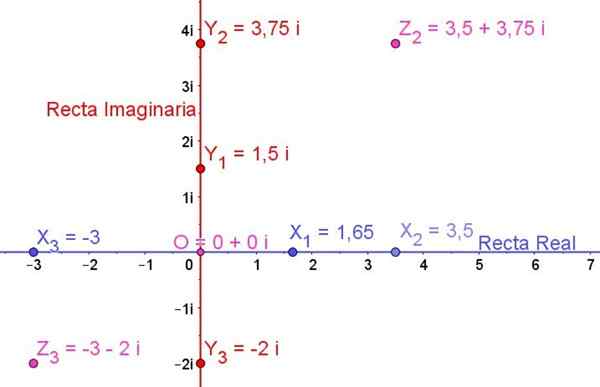Figur 1. Komplex plan som visar några verkliga siffror, några imaginära siffror och några komplexa siffror. Källa: f. Zapata.

I allmänhet uttrycks ett imaginärt nummer Z alltid i form: 

z = y⋅I

Var och Det är ett riktigt antal och Yo är den imaginära enheten.

Liksom verkliga siffror representeras på en linje, kallad Riktigt rakt, Analog de imaginära siffrorna representeras på Imaginär rak.

De Imaginär rak Det är alltid ortogonalt (90º form) till Riktigt rakt och de två linjerna definierar ett kartesiskt plan som kallas Komplex plan.

Figur 1 visar det komplexa planet och vissa verkliga siffror, vissa imaginära siffror och även några komplexa siffror representeras på det:

X₁, X₂, X₃ De är verkliga siffror

OCH₁, OCH₂, OCH₃ De är imaginära siffror

Z₂ och z₃ De är komplexa siffror

Antalet eller är den verkliga noll och är också den imaginära noll, så att ursprunget eller är nollkomplexet uttryckt av:

0 + 0i 

[TOC]

Egenskaper

Uppsättningen av imaginära siffror betecknas av:

I = ..., -3i, ..., -2i, .. .,-Yo, .. .,0i, .. .,Yo, .. .,2i, .. .,3i, ...

Och vissa operationer om denna numeriska uppsättning kan definieras. Ett imaginärt antal erhålls inte alltid från dessa operationer, så vi kommer att se dem med lite mer detaljer:

Summa och subtraktion av imaginära

Imaginära siffror kan lägga till och subtrahera från varandra och som ett resultat kommer det att finnas ett nytt imaginärt nummer. Till exempel:

Kan tjäna dig: relativa kusiner: vad är, förklaring, exempel

 3i + 2i = 5i

4i - 7i = -3i

Imaginär produkt

När produkten av ett imaginärt nummer med ett annat görs är resultatet ett verkligt antal. Låt oss göra följande operation för att kontrollera:

2i x 3i = 6 x i² = 6 x (√ (-1))² = 6 x (-1) = -6.

Och som vi ser är -6 ett verkligt tal, även om det har erhållits genom att multiplicera två rena imaginära siffror.

Produkt av ett riktigt nummer för en annan imaginär

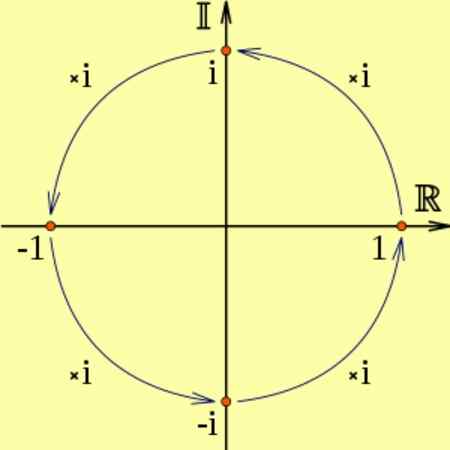
Om ett verkligt tal multipliceras med I kommer resultatet att vara ett imaginärt antal, vilket motsvarar en 90 graders rotation.

Och är det jag² motsvarar två på varandra följande rotationer på 90 grader, vilket motsvarar att multiplicera med -1, det vill säga² = -1. Det kan ses i följande diagram:

figur 2. Multiplikationen med den imaginära enheten och motsvarar 90º rotationer. Källa: Wikimedia Commons.

Till exempel:

-3 x 5i = -15i

-3 x i = -3i.

Förstärkning av en imaginär

Förstärkningen av ett imaginärt antal till en hel exponent kan definieras:

Yo¹ = jag

Yo² = i x i = √ (-1) x √ (-1) = -1

Yo³ = i x i² = -I

Yo⁴ = jag² x i² = -1 x -1 = 1

Yo⁵ = i x i⁴ = jag

I allmänhet måste du Yoⁿ = i^(n mod 4), var Mod Det är återstoden av uppdelningen mellan n och 4.

Förstärkningen av negativa heltal kan också göras:

Yo^-1 = 1 / i¹ = i / (i x i¹) = I / (i²) = I / (-1) = -i

Yo-² = 1 / i² = 1/ (-1) = -1

Yo-³= 1 / i³ = 1 / (-i) = (-1) / i = -1 x i^-1 = (-1) x (-i) = i

I allmänhet är det imaginära numret B⋅I höjt till kraft N:

(B⋅I) iⁿ = Bⁿ Yoⁿ = Bⁿ i^(n mod 4)

Några exempel är följande:

(5 i)¹² = 5¹² Yo¹² = 5¹² Yo⁰ = 5¹² x 1 = 244140625

(5 i)^elva = 5^elva Yo^elva = 5^elva Yo³ = 5^elva x (-i) = -48828125 i

(-2 i)¹⁰ = -2¹⁰ Yo¹⁰ = 2¹⁰ Yo² = 1024 x (-1) = -1024

Summan av ett verkligt antal och en imaginär

När ett verkligt nummer läggs till med en imaginär är resultatet varken verkligt eller imaginärt, det är en ny typ av nummer som heter Komplext tal.

Till exempel, om x = 3,5 och y = 3,75i, är resultatet det komplexa antalet:

Kan tjäna dig: minsta rutor

Z = x + y = 3,5 + 3,75 i

Observera att de verkliga och imaginära delarna inte kan grupperas i summan, så ett komplext antal kommer alltid att ha en verklig del och en annan imaginär del.

Denna operation utvidgar uppsättningen verkliga siffror till de bredaste komplexa siffrorna.

Ansökningar

Namnet på imaginära siffror föreslogs av den franska matematikern René Descartes (1596-1650) som ett hån eller oenighet med förslaget från dem som gjordes av den italienska matematikern från Raffaelle Century Bombelli.

Andra stora matematiker, som Euler och Leibniz, utstationerade Descartes i denna oenighet och kallas imaginära siffror som amfibiantal, som diskuterades mellan att vara och ingenting.

Namnet på imaginära siffror upprätthålls idag, men dess existens och betydelse är mycket verklig och påtaglig, eftersom de förekommer naturligt inom många fysikområden som:

-Relativitetsteorin.

-I elektromagnetism.

-Kvantmekanik.

Träning med imaginära siffror

- Övning 1

Hitta lösningarna på följande ekvation:

z² + 16 = 0

Lösning

z² = -16

Ta kvadratrot i båda medlemmarna du har:

√ (z² ) = √ (-16)

± z = √ (-1 x 16) = √ (-1) √ (16) = i x 4 = 4i

Med andra ord, lösningarna för den ursprungliga ekvationen är:

z = +4i eller z = -4i.

- Övning 2

Hitta resultatet av att höja imaginär enhet till Power 5 minus subtraktion Den imaginära enheten upphöjd till Power -5.

Lösning

Yo⁵ - Yo-⁵ = jag⁵ - 1/i⁵ = i - 1/i = i - (i)/(i x i) = i - i/( - 1) = i + i = 2i

- Övning 3

Hitta resultatet av följande operation:

(3i)³ + 9i 

Lösning

3³ Yo³ - 9 = 9 (-i) + 9i = -9i + 9i = 0i

- Övning 4

Hitta lösningarna på följande kvadratiska ekvation:

Kan tjäna dig: existens och unikhetsteorem: demonstration, exempel och övningar

(-2x)² + 2 = 0

Lösning

Ekvationen omorganiseras enligt följande:

(-2x)² = -2

Ta sedan en kvadratrot i båda medlemmarna

√ ((-2x)²) = √ (-2)

± (-2x) = √ (-1 x 2) = √ (-1) √ (2) = i √ (2) = √2 i

Sedan erhålls X äntligen:

x = ± √2 / 2 i

Det vill säga, det finns två möjliga lösningar:

x = (√2 / 2) i

Eller den här andra:

x = - (√2 / 2) i

- Övning 5

Hitta värdet på z definierad av:

Z = √ (-9) √ (-4) + 7

Lösning

Vi vet att kvadratroten för ett negativt verkligt antal är ett imaginärt antal, till exempel √ (-9) är lika med √ (9) x √ (-1) = 3i.

Å andra sidan är √ (-4) lika med √ (4) x √ (-1) = 2i.

Så att den ursprungliga ekvationen kan ersättas av:

3i x 2i - 7 = 6 i² - 7 = 6 (-1) -7 = -6 -7 = -13

- Övning 6

Hitta värdet på Z till följd av följande uppdelning av två komplexa nummer:

Z = (9 - i²) / (3 + i)

Lösning

Uttrycksnummer kan faktorera med hjälp av följande egenskap:

En skillnad mellan rutor är produkten av summan av skillnaden mellan binomialerna utan att höja torget.

Så:

Z = [(3 - i) (3 + i)] / (3 + i)

Det resulterande uttrycket förenklas sedan genom att återstår

Z = (3 - i)

Referenser

1. Earl, r. Komplexa tal. Återhämtat sig från: matematik.oxe.Växelström.Storbritannien.
2. Figuera, J. 2000. Matematik 1: a. Diversifierad. Co-bo-utgåvor.
3. Hoffmann, J. 2005. Urval av matematikfrågor. Monfort Publications.
4. Jiménez, r. 2008. Algebra. Prentice hall.
5. Wikipedia. Imaginär nummer. Hämtad från: i.Wikipedia.org