Decimalnotation

Den 3/2 fraktionen skriven i decimalnotation

Vad är decimal notation?

De decimalnotation Det består av att skriva ett riktigt nummer genom en hel del och en decimaldel, båda åtskilda av en punkt eller komma. Hela delen är vänster och decimaldelen till höger om den punkten.

0 kan visas både i hela delen och i decimalen. Följande siffror är till exempel decimalnummer:

• 0.25
• 1.5903
• 4,19367

Observera att decimaldelen av dessa siffror är begränsade, men det finns också siffror med en oändlig decimaldel, till exempel 0.33333 ..., där suspensiva punkter placeras som ett sätt att indikera att antalet decimaler fortsätter på obestämd tid.

I allmänhet kan ett ändligt decimalnummer skrivas som:

N.till₁till₂till₃Till ... till_n

Att vara ett heltal och n mängden decimaler, medan en oändlig decimal antar formen:

N.till₁till₂till₃..

I decimalen 0.25 identifieras:

• N = 0
• till₁ = 2
• till₂ = 5

Decimaler uppstår som ett annat sätt att uttrycka rationella siffror, som är de formade eller trasiga. I själva verket kan någon fraktion skrivas i decimalnotation, vilket kommer att ses omedelbart.

De tjänar också till att representera siffror som inte härstammar från en bråkdel, den så kallade irrationella siffror, som: π, √2, √3, √5, numret "e" och många andra.

Exempel på decimalnummer

Ett decimalnummer kan erhållas från en bråkdel på ett mycket enkelt sätt: beräkna kvoten på telleren mellan nämnaren. Om nämnaren är enheten följt av nollor är detta väldigt enkelt:

• 8/10 = 0.8
• - (5/100) = −0.05

I det första fallet, eftersom nämnaren är 10, placeras decimalpunkten omedelbart till vänster om 8 och decimal 0.8 läser "8 tiondelar" eller "nollpunkt åtta".

I det andra fallet, eftersom nämnaren är 100, måste du sätta decimalpunkten två platser till vänster om 5, och eftersom antalet är negativt, läser det "mindre 5 hundratals" eller "mindre nollpunkt fem".

När nämnaren inte är enheten följt av 0, används den långa uppdelningen:

Observera att för att utföra denna division, eftersom telleren är mindre än nämnaren, multiplicerades den först med 10 och därmed en 0 följt av decimalpunkten i kvoten, för att inte ändra operationen, så att inte som inte att ändra operationen. Fortsätt sedan normalt för att dela 10 med 2 vilket är lika med 5 och divisionsrester är 0.

Kan tjäna dig: vektorbelopp

Decimalformen av fraktion ½ är 0.5, att "nollpunkt fem" läses:

Fraktion 7/8 är ett annat exempel. Eftersom 7 är mindre än 8, multipliceras den 7 × 10 = 70, A 0 placeras i kvoten följt av decimalpunkten och är normalt uppdelad:

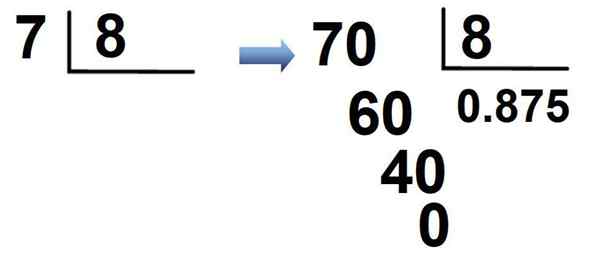
Resultatet är att fraktionen är skriven i decimal notation som:

7/8 = 0.875

Detta nummer, som det tidigare resultatet, är en ändlig decimal och ett sätt att läsa det är: "nollpunkt åtta hundra sjuttiofem". Genom denna procedur skrivs också följande fraktioner i decimalnotation:

8/10 = 0.8

5/7 = 0.714285714 ..

9/20 = 0.Fyra fem

3/8 = 0.375

Observera att som i alla dessa fraktioner är telleren mindre än nämnaren, hela delen av de resulterande decimalerna är 0. Men ett blandat tal eller ett Felaktig bråk (Att vars teller är större än nämnaren) också har decimalrepresentation.

I detta fall är hela delen större än eller lika med 1 om fraktionen är positiv och mindre än -1 om den är negativ:

9/4 = 2.25

10/3 = 3.333333 ..

−12/5 = −2.4

1 ½ = 1.5

2 ¾ = 2.75

Hela delen och fraktionerad del av de negativa decimalerna

I de tidigare exemplen observerades att för att hitta decimaluttrycket för en bråkdel är en teller och nämnaren helt enkelt uppdelade. Även om fraktionen är negativ, läggs helt enkelt minustecknet till motsvarande decimientuttryck.

Men hela delen och den fraktionella delen av en decimal skiljer sig åt beroende på det tecken du bär.

När en decimal är positiv, som 2.25, hela delen är 2 och dess decimaldel är 0.25 och numret kan skrivas som summan av hela delen och decimaldelen, så här:

2.25 = 2 + 0.25

Hela delen definieras som heltalet omedelbart lägre än decimalen och decimaldelen är alltid positiv. För 2.25, det omedelbart lägre heltalet är 2.

Men i fallet med fraktion −12/5, motsvarande decimalen −2.4 Ovanstående fungerar inte.

Kan tjäna dig: Vilka är delarna av det kartesiska planet?

 Om −2 var det hela delen och 0.4 Decimaldelen, genom att lägga till skulle erhållas:

−2 + 0.4 = −1.6 ≠ −2.4

Därför hela delen av −2.4 kan inte vara −2 men det omedelbart lägre heltalet: −3. Men i så fall skulle den fraktionella delen inte vara 0.4, eftersom genom att lägga till:

−3 + 0.4 = −2.6 ≠ −2.4

Så vad är decimaldelen av det negativa antalet −2.4? Det subtraherar decimalnumret från hela sin del och resultatet kommer alltid att vara positivt:

−2.4 - ( - 3) = 0.6

Slutligen är det bevisat att genom att lägga till hela delen och den fraktionella delen erhålls de sökande decimalerna:

−3 + 0.6 = −2.4

Förfarandet för att hitta en hel del och decimaldel av valfritt nummer, oavsett tecknet, sammanfattas på detta sätt:

• Hela delen är heltalet omedelbart lägre än decimalnumret.
• Decimaldelen beräknas genom att subtrahera decimalen från hela sin del.

För praktiska beräkningsändamål är emellertid decimalnumret −2.4 kan brytas ned som - (2 + 0.4) = - 24/10 eller:

Som framgår är inte decimalnoteringsrepresentationen av ett nummer unikt.

Typer av decimaler

Det finns decimalnummer vars decimaldel är begränsad eller oändlig, som används som klassificeringskriterier:

Ändliga eller exakta decimaler

När decimalerna är ändliga, till exempel 0.125, sägs det också att de är det exakta decimaler.

Oändliga decimaler

En oändlig decimal erhålls när återstoden av uppdelningen mellan teller och nämnaren aldrig görs 0.

Förutsatt att decimalen kommer från kvoten mellan två heltal, är denna decimal del periodisk, det vill säga den består av en eller flera siffror som upprepas på obestämd tid, kallas period.

Till exempel nummer 3.333333 ... härstammar av den felaktiga fraktionen 10/3, det är en periodisk decimal: hela delen är 3, och efter decimalpunkten upprepas numret 3 på obestämd tid på obestämd tid. Detta kan symboliseras genom att placera en kurva eller hatt på antalet som upprepas:

Perioden kan vara en större siffra, som i bråk 5/7, vars representation i decimalnotation är 0.71428571428571428 ... och det är skrivet som:

Kan tjäna dig: proportionell variation

Dessa decimaler där perioden visas omedelbart efter decimalpunkten kallas Rena periodiska decimaler. Men i detta annat:

Perioden, som är 45, föregås av två siffror som inte upprepas längre i decimaldelen: 23. Denna siffra kallas anteperiod, Eftersom det föregår perioden. I detta fall är det en Blandad tidnings decimal.

Slutligen finns det oändliga decimaler som inte är tidningar, som inte härstammar från kvoten mellan två hela siffror. Som nämnts i början tillhör dessa decimaler hela irrationella siffror, Som PI -numret, till exempel.

Löst övningar

Övning 1

Skriv numeriskt följande decimalnummer:

a) Nollpunkt fyra hundra fyrtio -sju
b) Fem tusendelar
c) Två enheter och fem hundratals
d) Tre punkt tjugo -sju negativa
e) En punkt åtta hundra tjugo tusen fem hundra sextio tre

• Lösning

a) 0.447

b) 0.005

c) 2.05

d) −3.27

e) 1.824563

Övning 2

Klassificera följande decimaler i exakta decimaler, rena tidningar, blandade tidningar eller irrationella nummer. I alla fall ange värdet på hela delen, och om de är tidningar eller blandade tidningar, ange också värdet på perioden och det främre, i förekommande fall:

a) 0.35627

b) 1.21212121 ..

c) −1.32

d) 1.414213562… = √2

• Lösning

a) 35627 är en exakt decimal. Hela delen är 0 och dess decimal är 0.35627.

b) 1.21212121 ... är en oändlig decimal och ren tidning, hela delen är 1 och perioden är 21.

c) −1.32 är en exakt och negativ decimal, vars hela del är −2. Decimaldelen beräknas genom att subtrahera decimalnumret från hela delen:

−1.32 - (−2) = 0.68

d) Decimaluttrycket av √2 är oändligt och inte periodiskt, eftersom det är ett irrationellt antal.

Det är en blandad tidning, hela delen är 3, den främre är 1 och perioden är 89.

Referenser

1. Pedagogiska bidrag och didaktiskt material. Decimalnotation. Återhämtat sig från: tecdigital.TEC.Växelström.Cr.
2. Baldor, a. 2007. Praktisk teoretisk aritmetik. Redaktionsgrupp Patria s.TILL. av C.V.
3. Matematik för handel. Förstå decimal notation. Hämtad från: OpenTextbc.Växelström.
4. Unk. Rationella siffror: Betydelser och representationer. Återhämtad från: Redi.Kodisk.Unk.mx.