Väntar på en linjeformel och ekvationer, representation, exempel

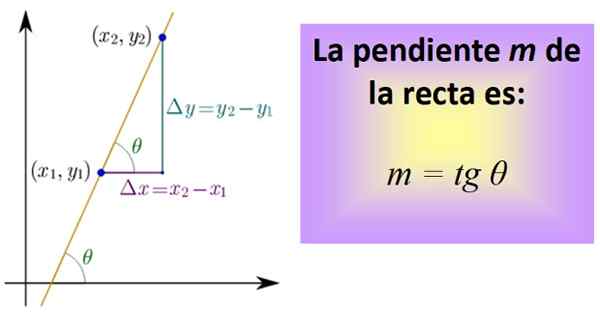
De avvänjning Det är tangenten i vinkeln θ att denna linje bildas med den horisontella axeln, som genom konventionen mäts i motsatt riktning till klockhänderna. Lutningen för vilken linje som helst är alltid konstant och det är därför det är en av dess mest väsentliga egenskaper.

För att beräkna det måste du veta två punkter i linjen, vars koordinater är (x x₁,och₁) och (x₂,och₂). Mellan båda punkterna dras ett segment som tillhör linjen och sedan dras de segment som representerar avståndet mellan x₁ och x₂, och mellan och₁ och och₂, som i den nedre figuren.

Figur 1. Linjens lutning är vinkelns tangent θ. Källa: Wikimedia Commons.

De tre segmenten utgör en höger triangel vars ben är: Δx = x₂ - x₁  och ΔY = och₂ - och₁. De motsvarar respektive en horisontell förskjutning och en annan vertikal.

Nu definieras en kvot, kallad tangent i vinkeln θ och förkortad tg θ, vilket är just lutningen m av linjen:

m = tg θ = Δy / Δx

Observera att för en linje förblir denna vinkel konstant, oavsett de punkter som tas för att beräkna dess tangent. I alla fall erbjuder detta värde oss ett mått på hur lutande det är linjen.

Genom koordinaterna för de valda punkterna kvarstår lutningsformeln:

M = (y - y₁ ) / (X₂ - x₁)

[TOC]

Grafisk representation

Nedan har vi flera situationer där begreppet sluttning är relevant. Dess värde kan enkelt beräknas genom att mäta respektive vertikal och horisontell förskjutning och sedan göra kvoten som anges i början.

Detta ger oss en uppfattning om lutningen eller nedgången av någon struktur, till exempel en ramp, ett tak eller en väg:

Kan tjäna dig: slumpmässig provtagning: metodik, fördelar, nackdelar, exempel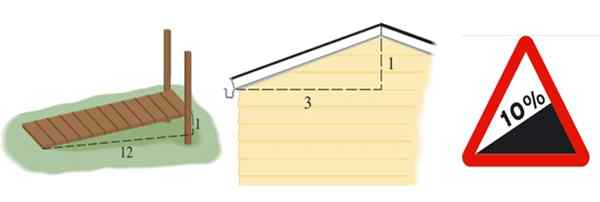 figur 2. Från vänster till höger lutningen på en ramp, ett tak och lutningen på en väg, den senare uttryckte i procent. Källa: Stewart, J. Precáculculo och Wikimedia Commons (rätt bild).

Rampens lutning som visas i figur 2 till vänster är M = 1/12, taket är M = 1/3 och vägen uttrycks i procent. En 10 % procent innebär att de för varje 100 meter som går framåt horisontellt tjänar 10 meter högt:

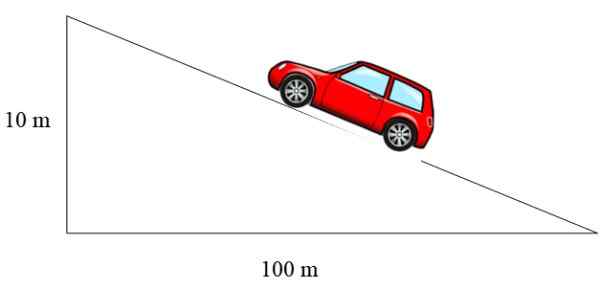Figur 3. Ett fordon stiger genom en lutning vars lutning är 10%. Källa: f. Zapata.

I detta fall är lutningen 10/100 = 0.1, som uttrycks i procent motsvarar 10%.

Typer av lutning

Linjens lutning kan vara positiv, negativ eller noll. Till exempel har linjen som visas i figur 1 en positiv lutning. Vi uppskattar det omedelbart eftersom vi ser att linjen är "lyft" om vi ser den från vänster till höger.

Om linjen går ner och ser den från vänster till höger, är lutningen negativ. Och när en linje är horisontell är dess lutning noll.

Slutligen, för vertikala linjer, är lutningen inte definierad.

Den grafiska representationen av varje typ finns nedan:

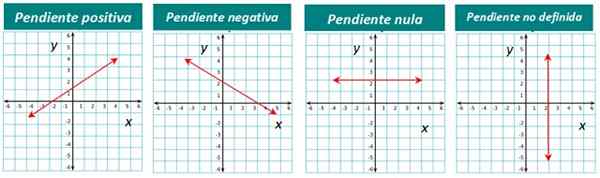Figur 4. Raderna enligt din sluttning. Källa: f. Zapata.

Hur beräknas lutningen en linje?

Att beräkna lutningen är väldigt enkel, du måste bara hitta vertikal förskjutning och horisontell förskjutning och sedan göra kvoten mellan de två.

När du har ritningen av linjen i det kartesiska planet väljer dessa förskjutningar alla två punkter i linjen P₁ Och s₂, Bestämma deras koordinater och tillämpa definitionen som gavs i början:

Kan tjäna dig: vad som representerar längden på hexagonförskjutning

M = (y - y₁ ) / (X₂ - x₁ )

Eftersom lutningens värde är oberoende av valet av P₁ Och s₂ , Vi kommer att välja en punkt P av koordinater (x, y) som tillhör linjen, vars koordinater inte är kända, och en annan punkt P₁ vars koordinater är: (x₁,och₁).

Lutningen är:

M = (y - y₁) / (x - x₁)

Vi kan rensa och:

och och₁ = m (x - x₁)

Anta nu punkten P₁ Det är skärningspunkten mellan linjen med den vertikala axeln, av koordinater (0, b). Ersätta detta i den tidigare ekvationen:

och - b = m (x - 0) → y = mx + b

Detta uttryck är känt som ekvationen för linjen i formen Väntande - skärningspunkt, Eftersom linjen är entydigt bestämd när dess lutning och skärning av den vertikala axeln är kända.

Att känna till bara lutningen räcker inte för att karakterisera en linje på planet, eftersom oändligt rakt kan ha samma lutning, vilket innebär att de är parallella, men gå igenom andra punkter.

Löst övningar

- Övning 1

Hitta lutningen på linjen som visas i följande figur:

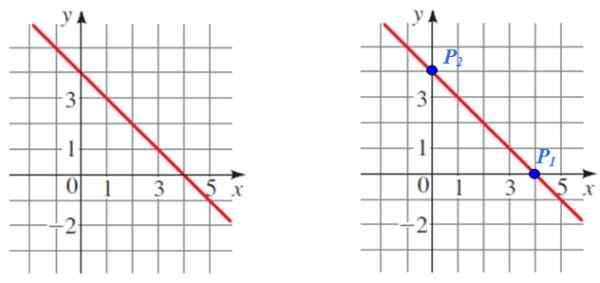Figur 5. Genom grafen för en rad väljs två punkter för att beräkna dess lutning. Källa: f. Zapata.

Lösning

P₁ Och s₂ De är två enkla -till -lästpunkter som kommer att tjäna för beräkningen, konstaterar också att de är respektive korsningar med koordinataxlarna.

Koordinaterna för varje punkt är:

P₁ (4.0) och P₂ (0,4)

Genom att ersätta lutningsekvationen:

M = (4 - 0) / (0 - 4) = 4 / ( - 4) = -1

Lutningen är negativ, vilket förväntades efter att ha observerat grafiken.

Kan tjäna dig: komplexa nummer: egenskaper, exempel, operationer

- Övning 2

Hitta ekvationen för linjen som passerar genom punkten (1, -6) och är parallell med linjen y = 2x - 3.

Lösning

Lutningen för den sökande linjen måste vara densamma som för y = 2x - 3, eftersom de är parallella. För denna linje är lutningen M = 2, därför har den vi letar efter formen:

och och₁ = 2 (x - x₁)

Nu ersätter vi den punkt genom vilken vår linje passerar: x₁ = 1 och₁ = -6.

och - (-6) = 2 (x - 1)

Därför y = 2x - 2 - 6 → y = 2x - 8

Exempel

Två mängder kan relateras på ett sådant sätt att din graf är en rak linje. I så fall sägs det att mängderna har linjärt beroende och lutningen på linjen kan tolkas som orsaken till förändringen av en variabel till den andra.

Exempel 1

Anta att en pool är fylld med vatten till en Betygsätta ständig i tid. Naturligtvis ju mer tid går, desto mer vatten lagras det. Tja, den hastighet som poolen är fylld är just lutningen för linjen som relaterar volymen till tid:

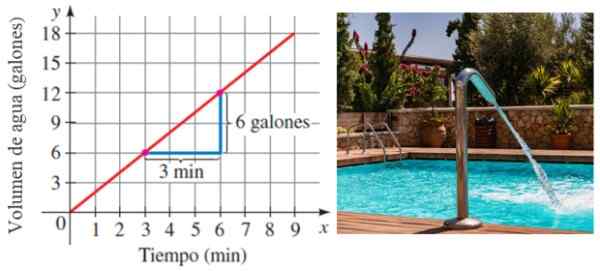Figur 6. Lutningen som en anledning till förändring. Källa: Stewart, J./Pxfuel.

I det här exemplet fylls poolen med en hastighet av 6/3 liter per minut eller 2 liter/minut.

Exempel 2

När en mobil rör sig i en rak linje med konstant hastighet beror lutningen för positionsgrafen på tiden är ingen annan än nämnda hastighet. Grafen visar en mobil med positiv hastighet, vilket innebär att den rör sig bort från ursprunget.

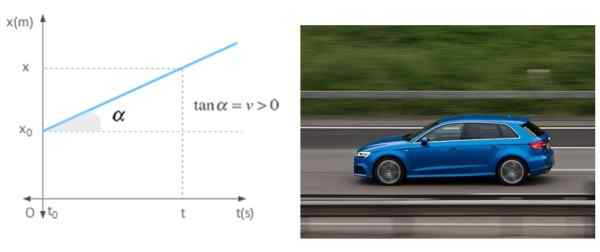Figur 7. Lutningen på kontra tidsgrafen är mobilens hastighet i en enhetlig rätlinjig rörelse. Källa: Wikimedia Commons/Pixabay.

Referenser

1. Alvarez, J. Lutningen på en väg. Återhämtat sig från: Geogebra.är.
2. Carena, m. 2019. Matematikhandbok för preuniversitet. National University of the Coast.
3. Hoffman, J. Urval av matematikfrågor. Volym 4.
4. Jiménez, r. 2008. Algebra. Prentice hall.
5. Stewart, J. 2006. Preccculment: Matematik för beräkning. Femte. Utgåva. Cengage Learning.
6. Zill, D. 1984. Algebra och trigonometri. McGraw Hill.