Tvärprodukt

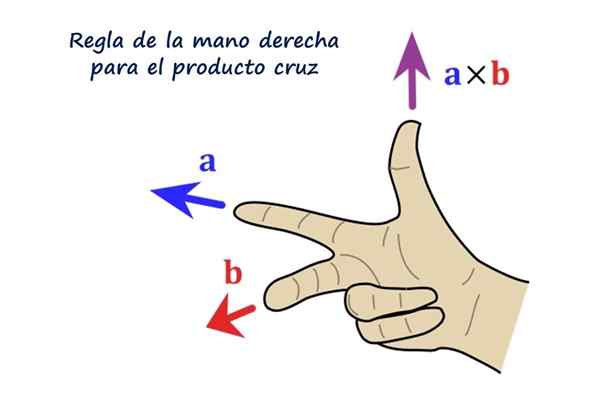Rätt regel för vektorprodukten. Källa: f. Zapata.

Vad är tvärprodukten eller vektorprodukten?

han Tvärprodukt, Även kallad Vector Product, det är en typ av produkt som utförs mellan två vektorer och resulterar i en annan vektor, vinkelrätt mot planet definierat av de två första.

Tvärprodukten mellan två vektorer till och b, Det resulterar i en annan vektor R, Matematiskt skrivs enligt följande:

till × b = R

Det läser så här: “En Cruz B lika med R ".

I tryckt text är vektorer skriven med djärva texter, eller med en pil på bokstaven, för att skilja dem från deras storlek eller modul. För detta används de, omväxlande, modulstänger och aktuella bokstäver, så det absoluta värdet på vektorn till Symbolen är skriven så här:

│till│ = a

Det absoluta värdet eller modulen för vektorprodukten mellan två vektorer beräknas genom att multiplicera modulen för båda vektorerna genom vinkeln θ mellan dem:

R = a ∙ b ∙ sen θ

Vektorns riktning R Det är vinkelrätt mot vektorerna till och b. Känslan av R Det är dextrogyr av till mot b Och i praktiken bestäms det med hjälp av högerhandens regel, som består av att placera index, medium och tumme på höger hand enligt följande:

• Pekfingret placeras efter vektorn till
• Med långfingret följer vektorn b
• Tummen, utökad, indikerar vektorns riktning och riktning R.

Denna ordning måste följas exakt, eftersom vektorprodukten inte är kommutativ, det vill säga till × b Sider b × till Och om vektorerna byts kommer inte rätt resultat att erhållas.

Kan tjäna dig: existens och unikhetsteorem: demonstration, exempel och övningar

Läsaren rekommenderas att placera sin högra hand som figuren visar, indexet som pekar till vänster representerar vektorn till, Långfingret följer b Och den pekar direkt på läsaren, slutligen indikerar tummen upp, pekar på vektorns riktning och riktning till × b = R.

Cruz produktegenskaper

-Kors- eller vektorprodukten mellan två vektorer resulterar alltid i en annan vektor.

-En tvärprodukt är därför inte kommutativ: till × b Sider b × till.

-För tvärprodukten är det sant att: till × b = - (b × till). Den här egenskapen kallas antikonminitet.

-Den resulterande vektorn för vektorprodukten mellan två vektorer är vinkelrätt (normal) till nämnda vektorer.

-Från ovanstående följer det att vektorprodukten mellan vektorer med samma riktning är noll. Särskilt till × A = 0.

-Korsprodukten uppfyller distributionslagen med avseende på summan: till × (b+c) = till × b + till × c

-Om M är en skalar, då M (till × b) = m till × b = till × m b

Korsprodukt mellan enhetsvektorer

De tre enhetsvektorerna, kallade Yo, J och k, De är vinkelräta mot varandra och anger de tre anmärkningsvärda riktningarna: hög, bred och djup. Dessa adresser är vinkelräta mot varandra.

Vektorprodukten mellan enhetsvektorerna bestäms lätt genom högerregeln och med tanke på korsproduktens egenskaper:

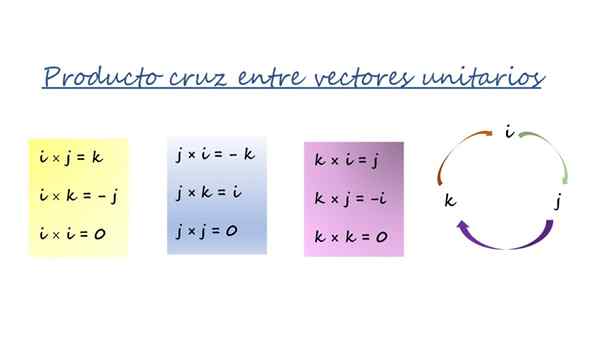Vektorprodukt av kartesiska enhetsvektorer. Källa: f. Zapata.

De tre färgade lådorna i figuren sammanfattas i omgången med pilar till höger och används på detta sätt:

-När du multiplicerar i pilens riktning är resultatet vektorn framför pilen och har ett positivt tecken. Till exempel genom att multiplicera vektor J och k, Den tredje vektorn är Yo, Och när beställningen följer meningen med pilen är tecknet +.

Kan tjäna dig: vektorfunktioner

-Och om den multipliceras i motsatt riktning till pilen är resultatet den tredje vektorn framför pilen, men med ett negativt tecken.

Enhetsvektorerna utgör en bas, så att alla andra vektor kan skrivas i termer av dem. Detta underlättar i hög grad beräkningen av tvärprodukten mellan två godtyckliga vektorer i rymden.

Hur man analyserar tvärprodukten från två vektorer analytiskt

När vektorer till och b De har en godtycklig riktning i rymden, med komponenter längs var och en av dem är det lättare att beräkna tvärprodukten på ett analytiskt sätt och uttrycka dem i termer av enhetsvektorerna Yo, J och k:

• till = a_x Yo + till_och J + till_z k
• b = B_x Yo + b_och J + b_z k

Nu används den distribuerande egenskapen för multiplikation, vilket också är giltigt för tvärprodukten:

till × b = (a_x Yo + till_och J + till_z k) × (b_x Yo + b_och J + b_z k) =

= (a_x Yo × b_x Yo) + (a_x Yo × b_och J) + (a_x Yo × b_z k) + (a_OCH J × b_x Yo) + (a_OCH J × b_och J) + (a_OCH J × b_z k) + (a_Z k × b_x Yo) + (a_Z k × b_och J) + (a_Z k × b_z k)

Korsprodukter mellan lika enhetsvektorer avbryts, eftersom de är parallella vektorer, vilket reducerar detta uttryck till 6 termer:

till × b = (a_x Yo × b_och J) + (a_x Yo × b_z k) + (a_OCH J × b_x Yo) + (a_OCH J × b_z k) + (a_Z k × b_x Yo) + (a_Z k × b_och J)

Slutligen, med siffran ovan, resulterar varje produkt i:

till × b = a_x b_och k + till_x b_z ( -J) + a_OCH b_x ( -k) + a_OCH b_z Yo + till_Z b_xJ + till_Z b_och ( -Yo) =

= (a_OCH b_z - a_Z b_och) Yo + (till_Z b_x - a_x b_z) J + (till_x b_och - a_OCH b_x) k

Cruz -produkt genom en determinant

Det är inte nödvändigt att memorera formeln ovan, men tillämpa bekvämt omgången av föregående figur eller helt enkelt genomföra den determinanten som visas nedan, vilket är helt motsvarande:

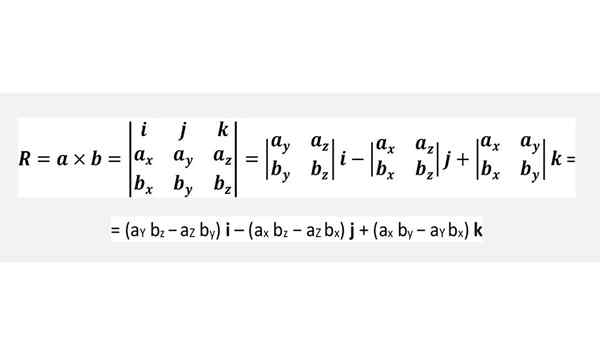
Exempel

Antagande vektorer till och b är:

• till = 5 Yo - J + 4 k
• b = -Yo + 0J +7 k

Korsprodukten mellan dem beräknas genom att identifiera och ersätta respektive koordinater:

Kan tjäna dig: Hyperbolic Paraboloid: Definition, Egenskaper och exempel

till_x = 5; till_och = −1; till_z = 4; b_x = −1; b_och = 0: B_z = 7

till × b = [(−1) ∙ 7 - 4 ∙ 0] Yo + [(4 ∙ (−1) - 5 ∙ 7) J + [5 ∙ 0 - (−1) ∙ (−1)] k = [−7 - 0] Yo + [(−4 - 35) J + [0 - 1] k =

= (−7) Yo - 39 J - k

Den determinantmetoden erbjuder samma resultat.

Träning

Beräkna med determinanter, tvärprodukten bland vektorerna:

• eller = 2 Yo +J + 5 k
• v = Yo + 4J +7 k

Och bestäm området för det parallellogram som är underlagt av de tidigare vektorerna, som visas i figuren:

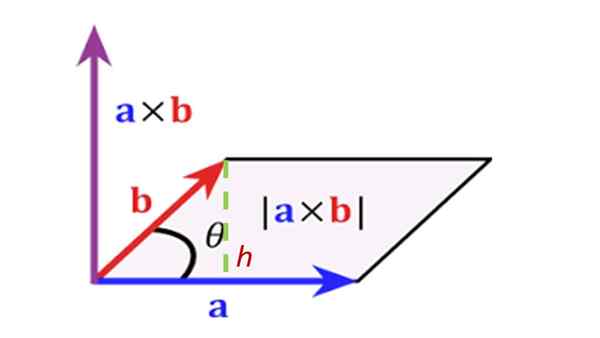
Lösning

Värden på vektorskoordinater ersätts i determinanten:

Det bestämda parallellogramområdet är modulen för vektorprodukten mellan dem, vilket resulterar: r = 17,3 areenheter.