Vad är dynamisk balans? (Med exempel)

han dynamisk balans Det är det tillstånd där ett mobilt objekt är idealiskt representerat som en partikel när dess rörelse är enhetlig rätlinjig. Detta fenomen inträffar när summan av yttre krafter som verkar på det avbryts.

Det tros vanligtvis att om det inte finns något netto eller resulterande kraft på ett objekt är vila den enda möjliga konsekvensen. Eller också att för att en kropp ska vara i balans bör det inte finnas någon kraftverkande.

Figur 1. Denna katt rör sig i dynamisk jämvikt om den gör det med konstant hastighet. Källa: Pixabay.

Egentligen är balansen frånvaro av acceleration, och därför är den ständiga hastigheten perfekt möjlig. Katten i figuren kan röra sig utan acceleration.

Ett objekt som har enhetlig cirkulär rörelse är inte i dynamisk jämvikt. Även om dess hastighet är konstant finns det en acceleration riktad mot mitten av omkretsen som håller den i banan. Denna acceleration är ansvarig för att korrekt bytas till hastighetsvektorn.

Nollhastighet är en speciell situation i balansen mellan en partikel, vilket motsvarar att bekräfta att objektet är i vila.

När det gäller att betrakta objekt som en partikel är det en mycket användbar idealisering när man beskriver deras globala rörelse. Egentligen består de mobila föremål som omger oss av ett stort antal partiklar vars individuella studie skulle vara besvärliga.

[TOC]

Superpositionsprincipen

Denna princip gör det möjligt att ersätta handlingen av flera krafter på ett objekt med en ekvivalent som kallas den resulterande kraften förkylning eller nettokraft FN och att i detta fall är ogiltigt:

F1 +F2 +F3 +.. . = Fr = 0

Där krafter F1, F2, F3 .. ., FI är de olika krafterna som verkar på kroppen. Sumory Notation är ett kompakt sätt att uttrycka det:

Så länge en obalanserad kraft inte ingriper kan objektet upprätthållas på obestämd tid i rörelse med konstant hastighet, eftersom bara en kraft kan förändra detta panorama.

När det gäller komponenterna i den resulterande kraften uttrycks det dynamiska jämviktstillståndet för en partikel enligt följande: fx = 0; Fy = 0; Fz = 0.

Rotations- och balansförhållanden

För partikelmodellen är tillstånd FR = 0 tillräcklig balansgaranti. Men när man tar hänsyn till dimensionerna på mobilen som studeras finns det möjligheten att objektet kan rotera.

Rotationsrörelsen innebär förekomsten av en acceleration, därför är de roterande kropparna inte i dynamisk jämvikt. Kroppens tur behöver inte bara en styrka, utan det är nödvändigt att tillämpa den praktiska webbplatsen.

För att kontrollera det kan du placera en tunn stång med längd på en yta fri från friktion, till exempel en isig yta eller en mycket polerad spegel eller glas. De normala balanserna på vikten vertikalt, och när du applicerar två krafter F1 och F2 av samma storlek, enligt diagrammet för följande figur, vad händer:

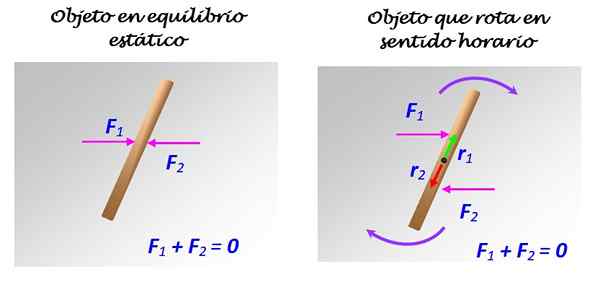figur 2. En stav på en yta utan friktion kan eller inte vara i balans, beroende på hur krafter 1 och 2 appliceras. Källa: Självgjord.

Om F1 och F2 gäller som visas till vänster, med en gemensam handlingslinje, kommer stången att förbli i vila. Men om F1 och F2 gäller som visas till höger, med olika handlingslinjer, även om det är parallellt, inträffar en rotation i ett schema, runt axeln som passerar genom mitten.

I detta fall utgör F1 och F2 ett par krafter eller helt enkelt ett par.

Vridmoment eller kraft av kraft

Effekten av vridmomentet är att producera en rotation på ett utökat objekt såsom exemplet Rod. Vektorstorleken som ansvarar kallas vridmoment eller också ett ögonblick av en kraft. Det betecknas som τ och beräknas av:

τ = r x f

I detta uttryck är F den applicerade kraften och R är vektorn som går från rotationsaxeln till appliceringspunkten (se figur 2). Riktningen för τ är alltid vinkelrätt mot planet där F och R ligger och dess enheter i internationellt system är N.m.

För exemplet är riktningen för de ögonblick som produceras av F1 och F2 mot papperet, enligt vektorproduktens regler.

Även om krafterna avbryter varandra gör deras vridmoment inte. Och resultatet är den som visas rotationen.

Jämviktsförhållanden för ett utökat objekt

Dessa är två villkor som måste uppfyllas för att garantera balansen mellan ett utökat objekt:

Löst exempel

Du har en låda eller bagageutrymme som väger 16 kg-F, som glider genom ett lutande plan med konstant hastighet. Kilens lutningsvinkel är θ = 36º. Svar:

a) Vad är storleken på den dynamiska friktionskraften som krävs för att bagaget ska glida med konstant hastighet?

b) hur mycket kostar den kinetiska friktionskoefficienten?

c) Om höjden h på det lutande planet är 3 meter, hitta hastigheten för nedstigning av stammen med vetskap om att det tar 4 sekunder att nå marken.

Lösning

Stammen kan behandlas som om det var en partikel. Därför kommer krafterna att gälla vid en punkt som ligger ungefär i centrum, på vilken all dess massa kan antas. Det är till denna punkt som spåret kommer att följas.

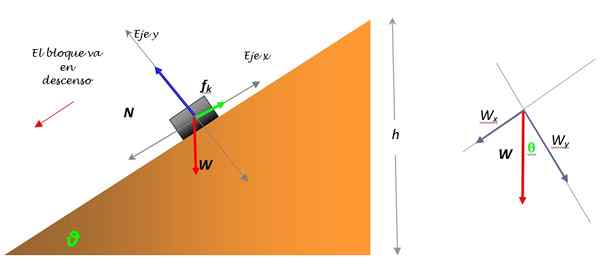Figur 3. Gratis kroppsdiagram för stammen som glider nedförsbacke och nedbrytning av vikt (till höger). Källa: Självgjord.

Vikten W är den enda kraften som inte faller på en av koordinataxlarna och måste delas in i två komponenter: WX och WY. Denna nedbrytning visas i schemat (figur 3).

Det är också bekvämt att passera vikten till enheterna i det internationella systemet, för vilket det räcker för att multiplicera med 9.8:

Wy = w.cosθ = 16 x 9.8 x cos 36º n = 126.9 n

Wx = w.Senθ = 16 x 9.8 x sin 36º = 92.2 n

Sektion A

Under hela den horisontella axeln finns den horisontella komponenten i WX -vikten och FK -dynamisk eller kinetisk friktionskraft, som motsätter sig rörelsen.

Att välja den positiva känslan i rörelsens riktning är det lätt att märka att det är WX ansvarigt för blocket att gå neråt. Och som friktionen motsätter sig, istället för att glida snabbt, har blocket möjlighet att glida ständigt nedförsbacke.

Det första jämviktstillståndet är tillräckligt, eftersom vi behandlar stammen som en partikel, som säkerställs i uttalandet som är i dynamisk jämvikt:

WX - FK = 0 (det finns ingen acceleration i den horisontella adressen)

Fk = 92.2 n

Avsnitt B

Storleken på dynamisk friktion är konstant och ges av fk = μk n. Detta innebär att den dynamiska friktionskraften är proportionell mot normal och storleken på detta krävs för att känna till friktionskoefficienten.

Observera det fria kroppsdiagrammet kan man se att vi på den vertikala axeln har den normala kraften n, som kilen utövar på stammen och riktas uppåt. Hon är balanserad med den vertikala komponenten i vikten WY. Att välja upp som en positiv mening och använda Newtons andra lag och balansstatus resulterar:

N - wy = 0 (det finns ingen rörelse längs den vertikala axeln)

Därför:

N = wy = 126.9 n

fk = μk n

μk = fk / n = 92.2/126.9 = 0.73

Avsnitt C

Det totala avståndet som reserats av stammen från toppen av kilen till marken hittas av trigonometri:

d = h/sin 36º = 3/sin 36º m = 5.1 m.

För att beräkna hastigheten används definitionen för enhetlig rätlinjig rörelse:

V = d/t = 5.1 m/4 s = 1.3 m/s

Referenser

1. Rex, a. 2011. Fysikens grunder. Pearson. 76 - 90.
2. Serway, R., Jewett, J. (2008). Fysik för vetenskap och teknik. Volym 1. 7th. Ed. Cengage Learning. 120 - 124.
3. Serway, R., Vule, c. 2011. Fysikens grunder. 9na ed. Cengage Learning. 99-112.
4. Tippens, s. 2011. Fysik: koncept och applikationer. Sjunde upplagan. Macgraw Hill. 71 - 87.
5. Walker, J. 2010. Fysik. Addison Wesley. 148-164.