Vad är förhållandet mellan romb- och rektangelområdet?

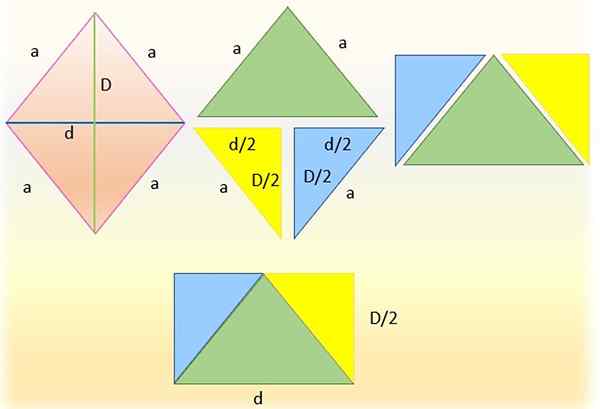
Sönderdelning av en romb för att få en rektangel. Källa: f. Zapata

Det är möjligt att beräkna rombområdet (och några andra geometriska figurer) från området för en triangel eller en relaterad fyrkantig, till exempel ett parallellogram eller en rektangel.

Rektangeln och parallellogramområdet är detsamma: det beräknas som produkten mellan figurens bas och dess höjd med avseende på den basen. Triangelområdet är för sin del.

Dessa formler är lätta att komma ihåg även om geometri naturligtvis erbjuder en exklusiv formel för rombområdet, och känner till måttet på dess stora och mindre diagonaler, betecknade som D respektive D:

Det är möjligt att härleda detta uttryck genom sekvensen som visas i figuren ovan.

För att göra detta skärs romben till vänster av en av dess diagonaler, som gjordes i figuren som sektionering av den mindre diagonalen, och därmed erhåller två trianglar. Den övre triangeln (i grönt) är kvar och den nedre är uppdelad i tur och ordning i två trianglar, skär i hälften av den stora diagonalen och får trianglarnas rektanglar identiska blå och gula.

Då sammanfaller hypotenuserna i dessa trianglar med sidorna på den gröna triangeln, eftersom de mäter samma, det vill säga "A". Och en rektangel erhålls äntligen, vars bas är den lägre "D" -diagonalen och vars höjd är hälften av den stora diagonalen, det vill säga: "D/2".

Rektangelområdet sammanfaller således sammanfaller exakt det för romb, därför kan det bekräftas att:

Kan tjäna dig: trinomial

TILL _diamant = (bas × höjd) _rektangel = D × (D/2)

Ett resultat som, som man kan se, sammanfaller exakt med formeln för rombområdet som ges tidigare.

Rombo och parallellogram område

Rhombus -området är också relaterat till ett parallellogram, eftersom båda geometriska figurerna är platta och tillhör familjen till fyrkantiga. Till exempel finns det i följande bild en romb till vänster och ett parallellogram till höger.

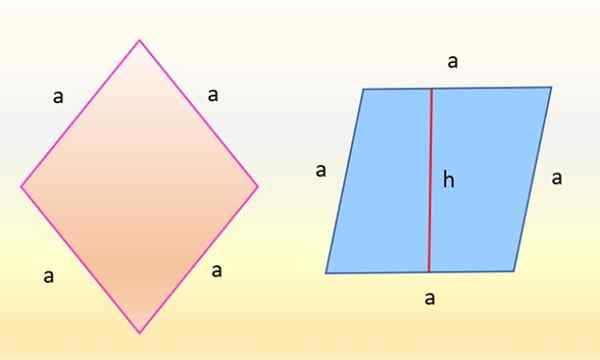Rombområdet till vänster är detsamma som för parallellogrammet till höger. Källa: f. Zapata

Det visar sig att siffrorna är identiska, eftersom det som har förändrats är bara orienteringen. Rhombus till vänster, i rosa, vars sidor har samma mått: a, det vänds på ett sådant sätt att en av dess sidor är helt horisontell. Sedan tar romben formen på det blå parallellogrammet till höger.

Och området för detta parallellogram är också produkten mellan basen "A" och höjden med avseende på den basen, kallad "H" i figuren, därför:

TILL _{parallellogram} = A × h

Eftersom det är samma siffra är området identiskt och följer det:

TILL _diamant = A × h

Således, kunskap och h av parallellogrammet, beräknas dess område och det kommer att sammanfalla med rombin.

Rombo -området inskrivet i en rektangel

En annan relation mellan romb och rektangel visas när den första är registrerad i den andra. Om detta händer sammanfaller rombens toppar med mittpunkten på sidorna av rektangeln, som visas nedan:

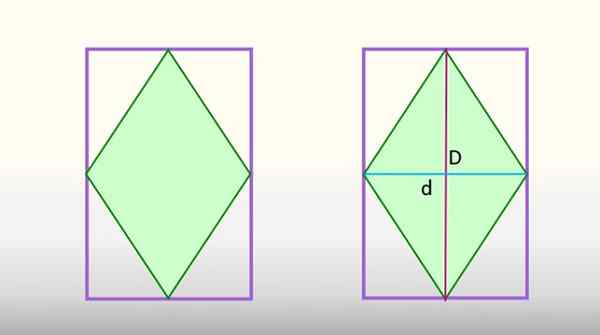Rombområdet inskrivet i rektangeln motsvarar hälften av rektangelområdet. Källa: f. Zapata

Denna bestämmelse gör de stora och mindre diagonalerna i romb, figuren är uppdelad i 8 identiska trianglar, varav 4 motsvarar romb, i grönt, och de andra 4 är en del av rektangeln. Om dessa sista fyra trianglar går ihop, skulle de bilda hälften av rektangeln och de fyra rombtrianglarna, den andra.

Det kan tjäna dig: Isosceles triangel

Därför motsvarar rombområdet hälften av rektangelområdet där det är registrerat och säger att:

TILL_diamant = A_rektangel / 2

Detta verifieras lätt genom att beräkna området för en av trianglarna och multiplicera med 4, eftersom de är identiska. Området för alla triangel är hälften av produkten mellan basen och dess höjd:

TILL _triangel = bas × höjd /2

Från föregående siffra observeras att basen för en av trianglarna är d/2 och höjden är d/2, som ersätter i den föregående formeln ger:

TILL _triangel = (d /2) × (d /2) /2 = (d × d) /8

Multiplicera detta resultat med 4 för att ha rombområdet:

TILL _diamant = 4 (d × d) /8 = (d × d) /2

För sin del är hälften av rektangeln:

TILL _rektangel / 2 = bas × höjd / 2

Eftersom basen för rektangeln är D och dess höjd är D, kvarstår den:

TILL_rektangel / 2 = D × D/ 2

Vilket är just området för den registrerade rombin. Då dras slutsatsen att:

Området för en romb som är registrerad i en rektangel motsvarar hälften av detta område.

Löst övningar

Övning 1

Hur mycket är rombområdet vars huvuddiagonala mätning 14.6 cm och den nedre diagonalen 9.8 cm?

Lösning

Genom att ersätta d = 14.6 cm och d = 9.8 cm i Rhombus Area -formeln:

Det sökande området är:

TILL _diamant = 14.6 cm × 9.8 cm = 143.1 cm²

Övning 2

I figuren av föregående sektion är huvuddiagonalen i romb som är registrerad i rektangelmätningen d = 30 cm och rektangelområdet är värt 210 cm². Det uppmanas att beräkna:

a) Längden på den mindre diagonalen

Det kan tjäna dig: linje och semi -flodsegment

b) Rombområdet, på två sätt: det första genom rektangelområdet och det andra med formeln för området för en romb. Kontrollera att resultatet är detsamma.

Lösning till

Rektangelområdet är produkten mellan dess bas och dess höjd. Den största diagonalen är dess höjd, medan den minsta diagonalen D skulle vara basen. Med hjälp av områdesformeln och ersätta värdena på uttalandet har du:

TILL _rektangel = bas × höjd = d × 30 cm = 210 cm²

Då är basen värd:

D = 210 cm² / 30 cm = 7 cm

Lösning B

Som ses ovan är rombområdet hälften av rektangelområdet, och detta är känt:

TILL _diamant = 210 cm² /2 = 105 cm²

Resultatet kontrolleras omedelbart och ersätter i formeln:

Diagonalerna är redan kända: D = 30 cm, d = 7 cm, sedan:

TILL _diamant = 30 cm × 7 cm /2 = 105 cm²

Det är bevisat att rombområdet som förväntat är detsamma i båda fallen.