Vad är algebraiska uttryck och vilka är de vanligaste?

De algebraiska uttryck De är matematiska termer som innehåller siffror och bokstäver. I kombination med symbolerna för matematiska operationer tillåter de att få formler eller ekvationer, från beskrivningar gjorda av ord. 

I sin tur kan dessa bokstäver läggas till, subtraheras, multipliceras eller divideras med andra siffror, som kan vara uttryckliga eller också representerade av bokstäver.

Figur 1. Exempel på algebraiska uttryck

[TOC]

Vad är algebraiska uttryck för?

Till exempel uttrycket:

2x + 3 

Det är ett algebraiskt uttryck, där bokstaven "X" representerar ett nummer som kanske är okänt eller som kan ta olika värden.

Vad är fördelen med att använda ett algebraiskt uttryck istället för att säga: "två gånger ett nummer läggs till 3"?

För det första upptar algebraiskt uttryck mindre utrymme. Och sedan, om X inte är ett fast nummer, kan olika värden ges till "X" för att få olika resultat av detta uttryck.

Detta kallas det numeriska värdet av algebraiskt uttryck.

Till exempel, om x = 1 är resultatet 2⋅1 + 3 = 2 + 3 = 5

Istället gör uttrycket x = -2 är 2⋅ (-2) + 3 = -4 + 3 = -1

I en annan typ av applikation representerar algebraiska uttryck en ekvation eller jämlikhet som måste lösas att veta värdet på antalet representerade av bokstaven.

Här har vi en enkel linjär ekvation:

2⋅x + 3 = 7

Lösningen på denna ekvation, som förresten också är ett algebraiskt uttryck, är:

x = 2

Eftersom multiplicering 2 by 2 ger 4 plus 3 ger resultatet: 7. Men det är lättare att förstå när ett algebraiskt uttryck används istället för att beskriva allt med ord.

Vanligaste algebraiska uttryck

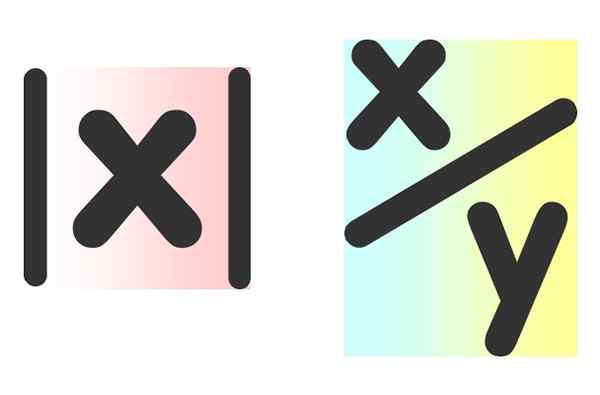figur 2. Okända mängder symboliserar ofta med bokstäverna "X" och "Y". Till vänster är det absoluta värdet på ett nummer och till höger kvoten i två siffror. Källa: Pixabay.

Algebraiska uttryck används allmänt i matematik, vetenskap, ekonomi och administration.

Nedan är en lista över uttryck som visas mycket ofta i matematik och andra ämnen, där ett förslag begärs eller löses.

Det kan tjäna dig: omkretsen av cirkeln: Hur man tar ut den och formler, lösta övningar

Vanligtvis betecknas ett okänt eller okänt nummer som "X", men vi kan använda alla andra alfabetbrev som överenskommits.

Det bör också komma ihåg att det i ett algebraiskt uttryck kan ha involverat mer än ett värde, okänt eller varierande, så var och en bör tilldelas ett annat brev.

Lista över algebraiska uttryck

-Det dubbla eller dubbla av ett nummer: 2x

-Duplet för ett antal fler enheter: 2m + 3

-Den tredje delen av ett nummer: Z/3

-Två gånger ett nummer utom dess tredje del: 2x - x/3

-Kvadratet för ett nummer: x²

-Kvadratet för ett antal mer av det numret: x² + 2x

-Duplet på kvadratet på ett nummer: 2x²

-Ett vridmomentnummer: 2n

-Ett udda nummer: 2n + 1

-Tre på varandra följande nummer: x, (x+1), (x+2)

-Tre på varandra följande jämna siffror: 2n, 2n +2, 2n +4

-Tre på varandra följande udda nummer, 2n + 1, 2n + 3, 2n + 5

-Ett visst nummer läggs till i följd: x +(x +1) = 2x +1

-Hälften av ett heltal: (x+1)/2

-Trippeln av hälften av kvadratet på ett nummer: 3. (1/2) x² = (3/2) x²

-Hälften av ytterligare ett antal av en annan: x/2 + y/3

-Den tredje delen av produkten mellan kvadratet för ett nummer och ett annat nummer som enheten subtraherades: (1/3) x².(Y-1)

-Ett nummer och dess motsats: a, -a

-Ett nummer och dess omvända: a, 1/a

-Summan av ett nummer med dess på varandra följande höjda till torget: x + (x + 1)²

-Subtrahera 7 vid två gånger ett visst nummer högt till torget: (2x)² - 7

-Två siffror som när det multipliceras ger 24: P.Q = 24

Kan tjäna dig: vinkelförskjutning

-Det absoluta värdet på ett nummer: │x│

-Kvoten mellan två siffror: x/y

-Kvadratroten för produkten av två nummer: √x.och

Figur 3. Detta algebraiska uttryck läses som "kvadratroten för produkten av två nummer x och y". Källa: Pixabay.

-Ett nummer som överstiger ett annat i 30 enheter: x = y +30

-Två gånger ett nummer som hans hälft subtraheras: 2x- x/2

Muntliga problem och deras algebraiska uttryck

- Problem 1

Hälften av en ko väger 100 kg mer än väger en fjärdedel av samma ko. Hur mycket väger ko?

Svar

För det algebraiska uttrycket för detta problem kallar vi x vikten på ko.

Hälften av ko väger ½ x. Fjärde delen av ko väger ¼ x. Slutligen är det algebraiska uttrycket som motsvarar: "Hälften av ko väger 100 kg mer än en fjärdedel" är:

½ x = ¼ x + 100

För att veta hur mycket ko väger måste du gruppera termerna med X på vänster sida och lämna 100 till höger:

(½ -¼) x = 100

¼x = 100

x = 400 kg

Ko väger 400 kg.

- Problem 2

På en gård är antalet kaniner dubbelt så många kor. Om antalet kor är 10. Hur många kaniner finns det?

Svar

Om C är antalet kaniner och V är antalet kor, är det algebraiska uttrycket för uttalandet:

C = 2⋅v

V = 10

Så ersätta värdet på V i den första av ekvationerna som det erhålls:

C = 2 ⋅ 10 = 20

Det vill säga gården har tjugo kaniner.

- Problem 3

Vad är antalet multiplicerat med sju och subtrahera sex ger tjugo -nine?

Svar

Om vi ​​kallar detta okända nummer X kan detta algebraiska uttryck höjs:

Kan tjäna dig: associativ egendom: summa, multiplikation, exempel, övningar

7x - 6 = 29

På den 6 vänstra sidan passerar den till höger sida av jämlikhet med ett förändrat tecken:

7x = 29 + 6 = 35

Det följer att x = 35/7 = 5

- Problem 4

Två gånger dras ett visst nummer 13 och 7 är 7. Vad är numret?

Svar

Om vi ​​kallar det nummer X, är dess algebraiska ekvation:

2 x - 13 = 7

Vad är värdet på 2x ?

Svaret är att 2x måste vara (13 + 7) så att när du tar bort 13 är det 7.

Detta innebär att 2x måste vara lika med 20, det vill säga:

2x = 20

Numret X som multipliceras med 2 Da 20 är därför 10:

x = 10

- Problem 5

Två på varandra följande heltal lägger till 23. Föreslå en algebraisk ekvation som gör det möjligt att bestämma numret och hitta det.

Svar

Anta att den första av siffrorna är n, så den som följer är n+1 och summan av dessa två är n+(n+1). Det är också känt att summan av summan är 23 då är ekvationen skriven:

n + (n + 1) = 23

Lösningen erhålls först förenkla den vänstra sidan av jämlikhet:

2 n + 1 = 23

Sedan rensas 2 N av 1 till höger medlem med det ändrade tecknet:

2 n = 23 - 1

Rätt medlem är löst:

2 n = 22

Därefter, n, som passerar de 2 som multiplicerar medlemmen i vänster som delar medlemmen i höger:

N = 22/2

Och det slutliga resultatet erhålls:

N = 11

Referenser

1. Baldor, a. Algebra. Centralamerikanska kulturella redaktionella c.TILL.
2. Carena, m. 2019. Matematikhandbok för preuniversitet. National University of the Coast.
3. Cimanet. Algebraiska uttryck. Återhämtat sig från: cinamet.Uoc.Edu
4. Guzman p. Algebraiska uttryck. Hämtad från: Finitionsbegrepp.av
5. Frågesport. Algebraiska uttryck. Återhämtad från: kanske.UPRM.Edu
6. Martha. Exempel på algebraiska uttryck. Återhämtat sig från: superprof.är