Område med en vanlig och oregelbunden Pentagon hur det tas, övningar

För att beräkna en pentagon Först måste vi avgöra om detta är regelbundet eller inte är. En Pentagon är en polygon, en stängd platt figur på fem sidor. När en polygon är regelbunden betyder det att längden på sidorna är densamma och dess inre vinklar också.

I så fall finns det en formel för att beräkna det exakta området för den vanliga polygonen, och känner till några av dess huvudsakliga egenskaper, som vi kommer att härleda senare.

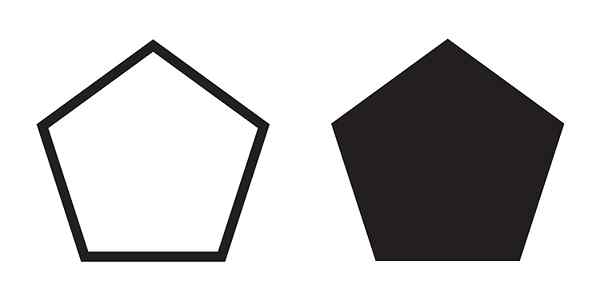Två pentagoner

Om polygonen inte är regelbunden, det vill säga den har sidor av olika storlekar och ojämlika inre vinklar, finns det ingen enda formel.

Men matematiker har hittat beräkningsstrategier, till exempel att dela upp figuren i andra med det lägsta antalet sidor, såsom trianglar, rutor och rektanglar, vars dimensioner är kända eller enkelt beräknade.

En annan procedur för att beräkna områden med polygoner i allmänhet, att känna till koordinaterna för dess vertikaler, är metoden som kallas Gauss determinanter, som vi kommer att beskriva senare.

[TOC]

Hur man beräknar området för en vanlig Pentagon?

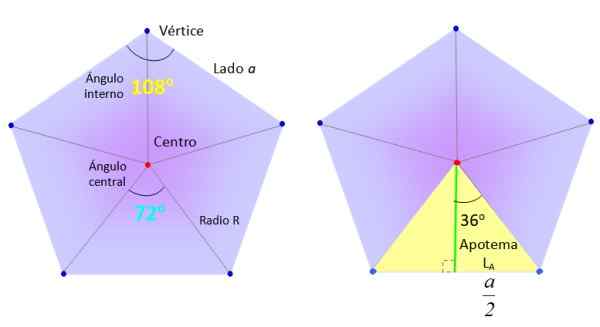
Vi kommer att ta en regelbunden Pentagon från sidan A, och vi kommer att dela upp den i 5 lika trianglar som visas i figuren, och drar segment från mitten (röd) till vertikterna (blå).

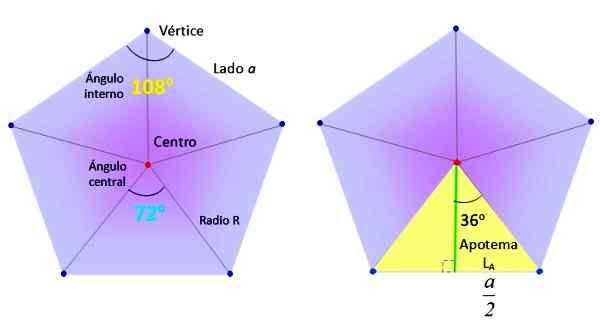De nödvändiga elementen för att hitta det vanliga Pentagon -området. Källa: f. Zapata.

I sin tur är trianglarna, såsom den enastående gula till höger i den övre figuren, uppdelade i två lika rektanglar, tack vare det gröna segmentet, kallad apotem.

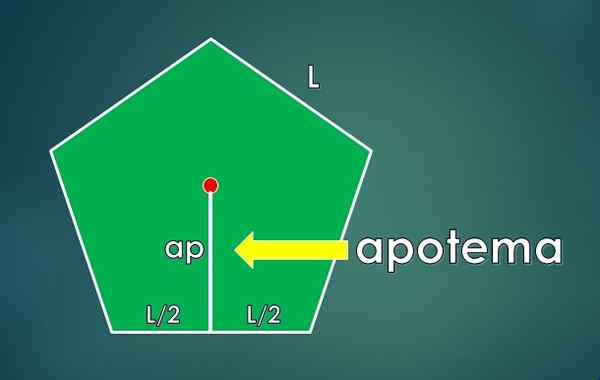
Apotheme definieras som det vinkelräta segmentet som ansluter till mitten av polygonen med mitten av ena sidan. Dess längd är L_TILL.

Området för en rektangel triangel av bas A/2 och höjd l_TILL är:

[(A/2) x l_TILL]

Pentagon har 10 trianglar som detta, därför är dess område:

Kan tjäna dig: vektorfunktioner

A = 10 (a/2) x l_TILL

Men omkretsen P av Pentagon är exakt P =10A, Därför ges området av halvprodukten i omkretsen och apotemens längd:

A = p x l_TILL /2

Vanligt Pentagon -område som känner till sidan a

Uttrycker längden på apotem l_TILL Beroende på sida A, att veta att den angivna vinkeln är halva den centrala vinkeln, det vill säga 36º, motsvarande:

36º = π/5

Genom elementär trigonometri, genom tangent av den akuta vinkeln 36º:

Solbränna (π/5) = (a/2) ÷ l_TILL

Därav:

L_TILL=  (A/2) ÷ solbrun (π/5)

Byte i det område som dras av i föregående avsnitt och veta att P = 5A:

A = p x l_TILL /2

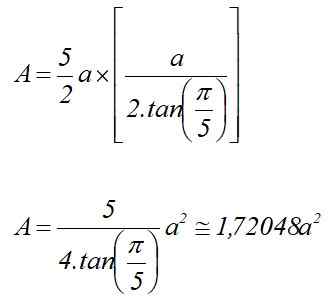
Regelbundet Pentagon -område som känner till sin radio

han radio av en vanlig polygon är det segment som går från mitten till en av dess vertikaler. Det sammanfaller med radien för den omskrivna omkretsen, som visas i följande figur:

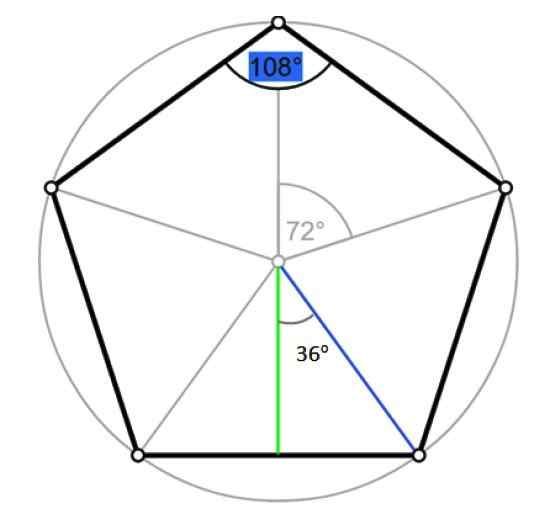Vinklar och apotem i Pentagon. Källa: Wikimedia Commons/F. Zapata.

Låt r vara måtten på nämnda radio, som sammanfaller med hypotenusen av den högra triangeln avgränsad i föregående figur, i blått. Av trigonometri:

cos 36º = cos (π/5) = l_TILL ÷ R

OCH

SIN 36º = SIN (π/5) = (A/2) ÷ R

Därför:

A = p x l_TILL /2 = 5r. sin (π/5) x r. cos (π/5) = 5r² [sin (π/5) x cos (π/5)]]

Använda dubbelvinkelformeln:

synd (2θ) = 2 sen θ . cos θ

Vi måste:

[sin (π/5) x cos (π/5)] = (1/2) sin 72º

Och så genom att ersätta detta värde får vi följande formel för det vanliga Pentagon -området:

A = (5/2) r².Sen 72º

Hur man beräknar området för en oregelbunden Pentagon?

Som vi har sagt tidigare, för en oregelbunden polygon finns det ingen enda formel, men det finns två metoder som vanligtvis fungerar mycket bra, den första kallas triangulering och den andra är metoden för Gauss -determinanter.

Kan tjäna dig: existens och unikhetsteorem: demonstration, exempel och övningar

Triangulering

Den består av att dela upp figuren i trianglar, vars område är lättare att beräkna, eller kan också testas med andra figurer vars område är känt, till exempel rutor, rektanglar och trapezider.

Gauss determinanter

Ett annat sätt att hitta det oregelbundna Pentagon -området eller annan oregelbunden polygon är att placera figuren i ett kartesiskt koordinatsystem för att hitta topparna för topparna.

Kända dessa koordinater, Gauss Determinants -metoden tillämpas för att beräkna området, som ges av följande formel:

Där a är området för polygon och (x_n , och_n ) är koordinaterna för vertikalerna. En polygon av N -sidor har 5 vertikaler, för Pentagon skulle det vara n = 5:

Stängerna som följer med formeln är modulstänger eller absolut värde.

Detta innebär att även om resultatet av operationen är negativt måste vi uttrycka det med ett positivt tecken, och om det redan är positivt måste det vara kvar med det tecknet. Detta beror på att ett område alltid är ett positivt belopp.

Förfarandet kallas Gauss -determinanter av dess skapare, den tyska matematikern Carl F. Gauss (1777-1855). De angivna operationerna motsvarar determinanten för en 2 × 2 -matris, till exempel den första determinanten är:

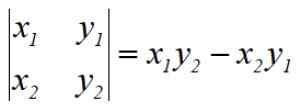
För att hitta Pentagon -området måste vi lösa 5 determinanter, lägga till resultatet algebraiskt, dela det med 2 och äntligen uttrycka området alltid med ett positivt tecken.

Löst övningar

Övning 1

Hitta det vanliga Pentagon -området vars apotem är värt 4 cm och vars sida mäter 5.9 cm.

Lösning

Eftersom det är en vanlig Pentagon, och vi har måtten på sidan och apotemet, använder vi den formel som har dragits av tidigare:

Kan tjäna dig: Scaleno Triangle

A = p x l_TILL /2

Omkrets P är lika med 5a = 5 x 5.9 cm = 29.5 cm.

A = 29.5 cm x 4 cm / 2 = 59 cm²

Övning 2

Hitta det oregelbundna Pentagon -området som visas. Följande dimensioner är kända:

DC ≈ av

AE = AB = 5

BC = 12

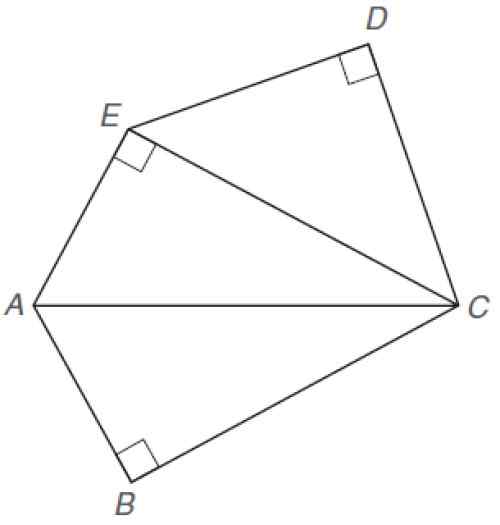Oregelbunden pentagon. Källa: Alexander, D. 2013. Geometri. Femte. Utgåva. Cengage Learning.

Lösning

Pentagon -området är summan av områdena i trianglarna, som är rektanglar. Uttalandet säger att DC ≈ för att därför när de tillämpar Pythagoras -teoremet på EDC -triangeln: Det har:

Ec² = 2 ed². Sedan EC = √2.Ed.

AEC- och ABC -trianglar har en gemensam hypotenus, som därför är AC -segmentet:

Tas² + Ec² = AB² + före Kristus²

Eftersom EA och AB mäter samma sak, erhålls det att:

EC = BC = √2.Ed

Sedan BC = 12, sedan ed = 12 / √2 = 8.485.

Med dessa värden kommer vi att beräkna området för varje triangel och lägga till dem i slutet.

EDC Triangle Area 

Ed x DC /2 = 8.485² / 2 = 36

AEC Triangle Area 

Ea x ec / 2 = ea x √2.Ed / 2 = 5 x √2. 8.485/2 = 30

ABC Triangle Area 

AB X BC / 2

Då är det sökta området:

5 x 12/2 = 30

Det är detsamma som Triangle AEC, eftersom båda har samma åtgärder.

Oregelbundet Pentagon -område

Slutligen är det begärda området summan av områdena i de tre trianglarna:

A = 36 + 30 + 30 enheter = 96 enheter.

Referenser

1. Alexander, D. 2013. Geometri. Femte. Utgåva. Cengage Learning.
2. Matematik öppen referens. Polygonområde. Återhämtat sig från: MathPenref.com.
3. Universumsformler. Area av en oregelbunden Pentagon. Återhämtat sig från: universalformulor.com.
4. Universumsformler. Område med en vanlig Pentagon. Återhämtat sig från: universalformulor.com.
5. Wikipedia. Pentagon. Återhämtad från: är.Wikipedia.com.