Magnetiska chockenheter, formler, beräkning, exempel

De magnetchock o Magnetmotstånd är oppositionen som ett medium presenterar passagen av magnetflödet: ju större det glänsande är det svårare att fastställa magnetflödet. I en magnetkrets har den glänsande samma roll som elektrisk motstånd i en elektrisk krets.

En spole som reste av en elektrisk ström är ett mycket enkelt magnetkretsexempel. Tack vare strömmen genereras ett magnetflöde som beror på den geometriska dispositionen av spolen och även på den nuvarande intensiteten som korsar den.

Figur 1. Magnetisk chock är ett kännetecken för magnetiska kretsar som transformatorn. Källa: Pixabay.

[TOC]

Formler och enheter

Betecknar magnetflödet som Φ_m, Du har:

Φ_m = N.I / (ℓ_c / μA_c)

Var:

-N är antalet spolens varv.

-Strömets intensitet är Yo.

-ℓ_c representerar kretslängden.

-TILL_c Det är tvärsnittsområdet.

-μ är miljöns permeabilitet.

Faktorn i nämnaren som kombinerar geometri plus miljöns inflytande är just den magnetiska chocken från kretsen, en skalär mängd som den betecknas med bokstaven ℜ, för att skilja den från det elektriska motståndet. Så:

ℜ = ℓ_c / μ.TILL_c

I det internationella enhetssystemet (SI) mäts det till ℜ som det omvända av Henrio (multiplicerat med antalet varv N). I sin tur är Henrio enheten för magnetisk induktans, motsvarande 1 Tesla (t) x kvadratmeter /amperio. Därför:

1 TIMME^-1 = 1 a /t.m²

 Som 1 t.m² = 1 Weber (WB), den glänsande uttrycks också i A/WB (Amperio/Weber.

Hur beräknas magnetisk chock?

Eftersom den magnetiska chocken har samma roll som elektrisk motstånd i en magnetkrets är det möjligt att utöka analogin med en motsvarande OHM V = gå för dessa kretsar.

Kan tjäna dig: manometriskt tryck: förklaring, formler, ekvationer, exempel

Även om det inte cirkulerar ordentligt, magnetflödet φ_m ta platsen för strömmen, medan istället för spänning V, De Magnetspänning antingen Magnetomotor, analog elektromotor eller F.och.m I elektriska kretsar.

Magnetomotor Force ansvarar för att upprätthålla magnetflödet. Det är förkortat F.m.m Och det betecknas ℱ. Med det har du äntligen en ekvation som relaterar de tre storleken:

ℱ = φ_m . ℜ

Och jämföra med ekvationen Φ_m = N.I / (ℓ_c / μA_c), det dras slutsatsen att:

ℱ = n.Yo

På detta sätt kan det glänsande beräknas med att känna till kretsens geometri och miljöns permeabilitet, eller också att känna till magnetflödet och den magnetiska spänningen, tack vare den sista ekvationen, kallad Hopkinson Law.

Skillnad med elektrisk motstånd

Ekvationen av MRI ℜ = ℓ_c / μA_c Det liknar  R = l / σa För elektrisk motstånd. I det senare representerar σ materialets konduktivitet, L är trådens längd och A är området för dess tvärsnitt.

Dessa tre storlekar: σ, l och a är konstant. Men miljöns permeabilitet μ, I allmänhet är det inte konstant, så att den magnetiska chocken från en krets inte är, till skillnad från dess elektriska simil.

Om det sker en förändring från mediet, till exempel när du passerar från luft till järn eller vice versa, är det en förändring i permeabiliteten, med den därmed variationen i det glänsande. Och även magnetiska material går igenom Hysterescykler.

Detta innebär att tillämpningen av ett externt fält får materialet att behålla en del av magnetismen, även efter fältet.

Det är därför varje gång den magnetiska chocken beräknas är det nödvändigt att noggrant specificera vid vilken punkt i cykeln materialet är och därmed vet dess magnetisering.

Kan tjäna dig: Fysisk optik: Historia, ofta villkor, lagar, applikationer

Exempel

Även om de glänsande beror mycket på kretsens geometri beror det också på mediumets permeabilitet. Ju större värde på detta, desto lägre är det blanka; Sådant är fallet med ferromagnetiska material. Luften för sin del har låg permeabilitet, därför är dess magnetiska chock större.

Magnetventil

En magnetventil är en galen längd ℓ gjord med n varv, genom vilken en elektrisk ström passeras och. Svängarna rullas vanligtvis cirkulärt.

Inuti ett intensivt och enhetligt magnetfält genereras, medan fältet görs ungefär noll.

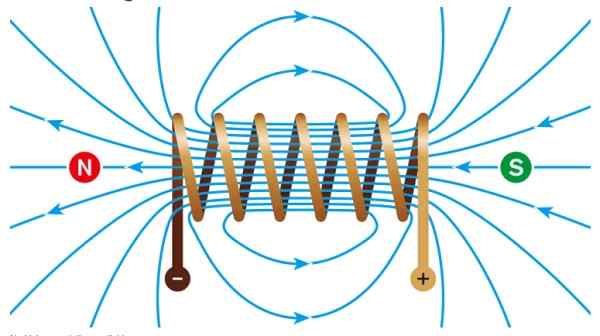figur 2. Magnetfält inuti en magnetventil. Källa: Wikimedia Commons. Rajiv1840478 [CC BY-S (https: // Creativecommons.Org/licenser/BY-SA/4.0)].

Om en cirkulär form ges en cirkulär form finns det en Toroid. Inuti kan det finnas luft, men om en järnkärna placeras är magnetflödet mycket större, tack vare den höga permeabiliteten för detta mineral.

Rullad spole på en rektangulär järnkärna

En magnetkrets kan byggas genom att lindas spolen på en rektangulär järnkärna. På detta sätt, när en ström passeras genom tråden, är det möjligt att upprätta ett intensivt fältflöde begränsat inuti järnkärnan, vilket kan ses i figur 3.

Shilling beror på kretslängden och tvärsnittet som anges i figuren. Kretsen som visas är homogen, eftersom kärnan är av ett enda material och tvärsnittet förblir enhetlig.

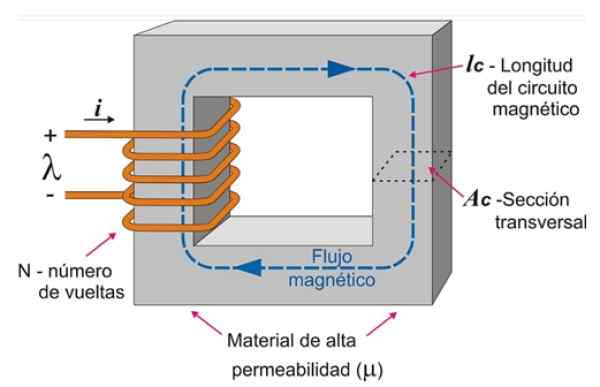Figur 3. En enkel magnetkrets bestående av en spole överväldigad på en järnkärna rektangulär. Källa till vänster figur: Wikimedia Commons. Ofta [CC BY-SA (https: // CreativeCommons.Org/licenser/BY-SA/3.0)]

Löst övningar

- Övning 1

Hitta den magnetiska chocken från en 2000 spiral rätlinär magnetventil, veta att genom att cirkulera en ström på 5 a magnetflöde av 8 MWB genereras.

Kan tjäna dig: elektromagnetiska vågor: Maxwell teori, typer, egenskaper

Lösning

Ekvation används ℱ = n.Yo För att beräkna magnetspänningen, eftersom intensiteten hos strömmen och antalet varv i spolen är tillgängliga. Det multipliceras helt enkelt:

ℱ = 2000 x 5 a = 10.000 ampere-vuelta

Sedan användning av ℱ = φ_m . ℜ, Att se till att uttrycka magnetflödet i Weber (prefixet "M" betyder "Mili", så det multipliceras av 10 ^-3:

Φ_m = 8 x 10 ^-3 Wb

Nu rensas chocken och värdena ersätts:

ℜ = ℱ/ φ_m = 10.000 AMPS-vuelta /8 x 10 ^-3 WB = 1.25 x 10⁶ Amperio-Vuelta/WB

- Övning 2

Beräkna den magnetiska chocken från kretsen som visas i figuren med de dimensioner som visas, som är i centimeter. Kärnans permeabilitet är μ = 0.005655 t · m/a och tvärsnittet är konstant, 25 cm².

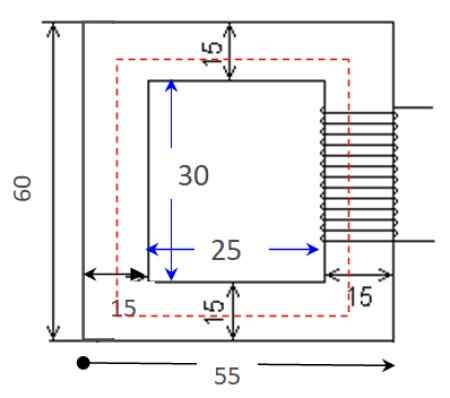Figur 4. Magnetkrets av exempel 2. Källa: f. Zapata.

Lösning

Vi kommer att tillämpa formeln:

ℜ = ℓ_c / μA_c

Permeabiliteten och tvärsektionsområdet finns tillgängliga som data i uttalandet. Vi måste hitta kretslängden, som är omkretsen av den röda rektangeln i figuren.

För att göra detta är längden på en horisontell sida medelvärde, vilket ger större längd och lägre längd: (55 +25 cm)/2 = 40 cm. Fortsätt sedan på samma sätt för den vertikala sidan: (60 +30 cm)/2 = 45 cm.

Slutligen läggs de genomsnittliga längderna på de fyra sidorna till:

ℓ_c = 2 x 40 cm + 2 x 45 cm = 170 cm

Det återstår att ersätta värden i orten, men inte innan du uttrycker längd och område på tvärsnittet - som ges i uttalandet - i enheter om:

ℜ = 170 x 10 ^-2m / (0.005655 t · m/a x 0.0025 m²) = 120.248 AMPERIO -VUELTA/WB

Referenser

1. Tyska, m. Ferromagnetisk kärna. Återhämtat sig från: YouTube.com.
2. Magnetkrets och motvilja. Återhämtad från: MSE.Ndhu.Edu.Tw.
3. Spinadel, e. 1982. Elektriska och magnetiska kretsar. Ny bokhandel.
4. Wikipedia. Magnetomotor. Återhämtad från: är.Wikipedia.org.
5. Wikipedia. Magnetchock. Återhämtad från: är.Wikipedia.org.