Teleskop sommar hur det löses och löses övningar

De summering Teleskopisk Det är en gren av operationer med numeriska serier. Behandlar sammanfattningar av element från ett initialvärde till "n" av uttryck vars argument beror på något av följande mönster:

(F_x - F_x+1); F_x+1  - F_x)

Där dess sammanfattande uttryck definieras enligt följande: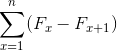

Också:

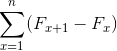
Källa: Pixabay.com

De representerar en summa av element som, när de utvecklas, är föremål för avbokningar av motsatta termer. Orsakar följande jämlikhet för teleskopsumma:

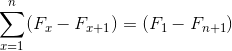
Namnet kommer från förhållandet till utseendet på ett klassiskt teleskop, som kan vikas och distribueras, vilket avsevärt förändrar dess dimension. På liknande sätt kan teleskopiska sammanfattningar, som i deras natur är oändliga, sammanfattas i förenklat uttryck:

F₁ - F_N+1

[TOC]

Demonstration

När man utvecklar summan av termer är eliminering av faktorer ganska uppenbar. Var för vart och ett av fallen kommer motsatta element att visas i följande iteration.

Det första fallet kommer att tas som ett exempel, (f_x - F_x+1), eftersom processen fungerar homolog med (f_x+1-F_x).

Utveckla de första 3 värdena 1, 2, 3 förenklingstendensen observeras

X₁     (F₁ - F₁₊₁) = F₁ - F₂

X₂     (F₂ - F₂₊₁) = F₂ - F₃

X₃     (F₃ - F₃₊₁) = F₃ - F₄

Var genom att uttrycka summan av de beskrivna elementen:

X₁ + X₂ + X₃ = F₁ - F₂ + F₂ - F₃ + F₃ - F₄

Det observeras att termerna f₂ och f₃ De beskrivs med sina motsatser, vilket gör deras förenkling oundviklig. På samma sätt som det observeras att termerna f₁ och f₄ förbli.

Om summan gjordes av x = 1 till x = 3 betyder det att elementet f₄ motsvarar den generiska termen f_N+1.

Således visar jämlikhet:

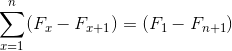
Hur är det löst?

Syftet med teleskopssamtal är att underlätta arbetet, så att det inte är nödvändigt att utveckla en oändlig mängd termer, eller förenkla en för lång kedja.

Kan tjäna dig: Trachtenberg Method: Vad är det, exempel

För upplösning kommer det bara att vara nödvändigt att utvärdera termer f₁ och f_N+1. Dessa enkla ersättningar utgör det slutliga resultatet av summan.

Helheten i termerna kommer inte att uttryckas, vilket blir nödvändigt för demonstrationen av resultatet, men inte för den normala beräkningsprocessen.

Det viktiga är att märka konvergensen i den numeriska serien. Ibland kommer inte summan att uttryckas på ett teleskopiskt sätt. I dessa fall är implementeringen av alternativa faktoriseringsmetoder mycket vanligt.

Den karakteristiska faktoriseringsmetoden i teleskops sammanfattningar är den för enkla fraktioner. Detta inträffar när en originalfraktion sönderdelas till en summa av flera fraktioner, där det teleskopmönstret kan observeras (F_x - F_x+1) eller (f_x+1  - F_x).

Nedbrytning i enkla fraktioner

För att verifiera konvergensen i numeriska serier är det mycket vanligt att omvandla rationella uttryck med den enkla fraktionsmetoden. Målet är att modellera argumentet fram till formen av en teleskopisk sammanfattning.

Till exempel representerar följande jämlikhet en nedbrytning i enkla fraktioner:

När du utvecklar den numeriska serien och tillämpar motsvarande egenskaper tar uttrycket enligt följande:

Där teleskopformen kan ses (f_x - F_x+1).

Förfarandet är ganska intuitivt och består i att hitta värdena på telleren som, utan att bryta jämlikheten, tillåter att separera de produkter som finns i nämnaren. Ekvationerna som uppstår vid bestämningen av dessa värden höjs enligt jämförelser mellan båda sidor av jämlikhet.

Denna procedur observeras steg för steg i utvecklingen av övning 2.

Kan tjäna dig: 6 roliga matematiska gåtor för barn

Historia

Det är ganska osäkert att kunna definiera det historiska ögonblicket där de teleskopiska sammanfattningarna presenterades. Emellertid börjar implementeringen ses under sjuttonhundratalet, i numeriska serier som genomfördes av Leibniz och Huygens.

Båda matematiker, när man utforskar sammanfattningarna av triangulära siffror, börjar märka trender i konvergensen av vissa serier av successiva element. Men ännu mer intressant är början på modelleringen av dessa uttryck, i element som inte nödvändigtvis händer.

Faktum är att uttrycket som tidigare använts för att hänvisa till enkla fraktioner:

Det presenterades av Huygens och kallades omedelbart Leibnizs uppmärksamhet. Som med tiden kunde observera konvergensen till värde 2. Utan att veta det implementerade det den teleskopiska sammanfattningen.

Övningar

Övning 1

Definiera vilken term Följande summa konvergerar:

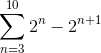
När summan utvecklas manuellt observeras följande mönster:

(2³ - 2⁴) + (2⁴ - 2⁵) + (2⁵ - 2⁶) ... (2¹⁰ - 2^elva)

Där faktorerna från 2⁴ upp till 2¹⁰ De presenterar positiva och negativa delar, vilket gör deras avbokning tydlig. Då kommer de enda faktorerna som inte kommer att förenklas att vara den första “2³"Och den sista" 2^elva".

På detta sätt, vid implementeringen av de teleskopiska sammanfattningskriterierna, erhålls det:

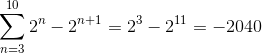
Övning 2

Förvandla argumentet till en teleskopisk typ -summa och definiera seriens konvergens:

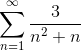
Som anges i uttalandet kommer det första att vara att sönderdelas i enkla fraktioner för att tänka om argumentet och uttrycka det i en teleskopisk form.

2 Fraktioner vars nämnare är “N” och ”N+1” måste hittas, där metoden som används nedan måste uppnå värdena på telleren som uppfyller jämlikhet.

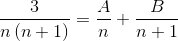
Värdena på A och B definieras. Första summan av fraktioner görs.

Kan tjäna dig: 60 delare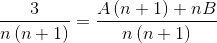

Sedan förenklas nämnare och en linjär ekvation upprättas.

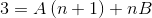
I nästa steg drivs uttrycket av höger, tills ett mönster som är jämförbart med "3" till vänster.

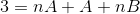
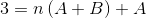
För att definiera de ekvationer som ska användas måste resultaten från båda sidor av jämlikhet jämföras. Det vill säga inga variabla n -värden observeras på vänster sida, på detta sätt måste A +B vara lika med noll.

A + B = 0; A = -b

Å andra sidan måste det konstanta värdet vara lika med konstant värde 3.

A = 3

Därför.

A = 3 och b = -3

Redan definierade värdena på telleren för enkla fraktioner, summan är omprövad.

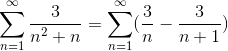
Där den generiska formen av teleskopsumma redan har uppnåtts. Teleskopserien är utvecklad.

Var genom att dela med ett mycket stort antal kommer resultatet att ungefärliga mer och mer, observera seriens konvergens till värde 3.

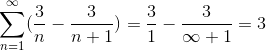
Denna typ av serie kunde inte lösas med andra ord på grund av den oändliga mängden iterationer som definierar problemet. Men denna metod, tillsammans med många andra inramar grenen av studien av den numeriska serien, vars mål är att bestämma konvergensvärdena eller definiera skillnaden i dessa serier.

Referenser

1. Infinitesimal beräkningslektioner. Manuel Franco, Manuel Franco Nicolás, Francisco Martínez González, Roque Molina Legaz. Editum, 1994.
2. Omfattande beräkning: successioner och serier av funktioner. Antonio Rivera Figueroa. Patria Redaktionsgrupp, 21 oktober. 2014.
3. En kurs i kalkyl och verklig analys. Sudhir r. Ghorpade, Balmohan V. Limaye. Springer Science & Business Media, 5 juni. 2006.
4. Oändlig serie. Tomlinson Fort. Clarendon Press, 1930.
5. Delar av teorin om oändliga processioner. Lloyd Leroy Smail. McGraw-Hill Book Company, Incorpan, 1923.