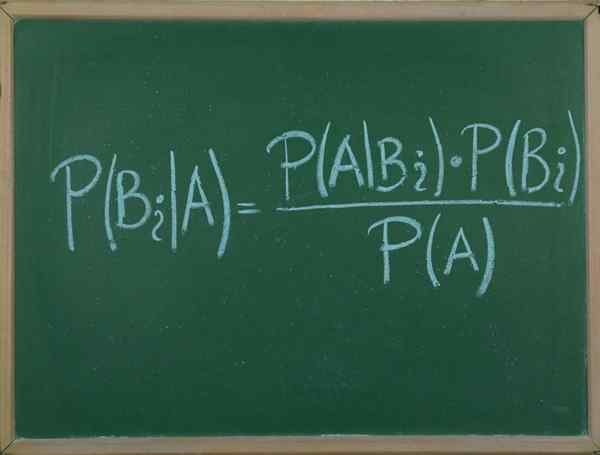Bayes teorem
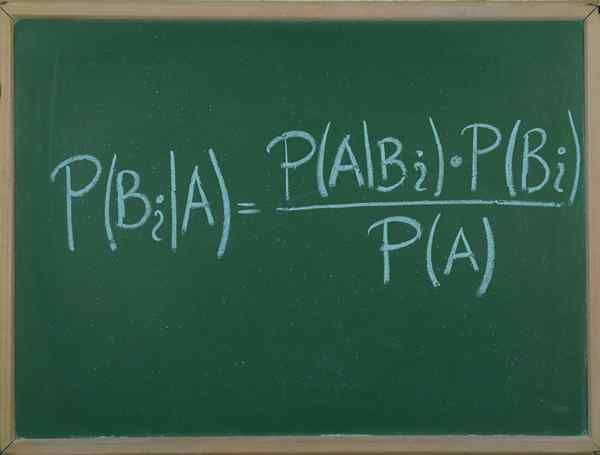
- 3088
- 599
- Johan Johansson
Vi förklarar vad som är Bayes teorem, dess tillämpningar och vi lägger övningar löst
Vad är Bayes teorem?
han Bayes teorem Det är en procedur som gör att vi kan uttrycka den villkorade sannolikheten för en slumpmässig händelse en tärning B, i termer av sannolikhetsfördelningen av händelse B som ges och sannolikhetsfördelningen endast till.
Detta sats är mycket användbart, eftersom vi tack vare det kan relatera till sannolikheten för att en händelse A händer med att veta att B hände, med sannolikheten för att det motsatta inträffar, det vill säga att det inträffar till.
Bayes 'sats var ett silverförslag av pastor Thomas Bayes, en artonde århundradet engelska teolog som också var matematiker. Han var författare till flera Jobs in Theology, men för närvarande är han känd för ett par matematiska fördrag, bland vilka Bayes teorem redan nämnt som ett huvudresultat.
Bayes handlade om detta teorem i ett verk med titeln "En uppsats mot att lösa ett problem i doktrinen om chanser" (en uppsats för att lösa ett problem i doktrinen om möjligheterna), publicerad 1763, och på vilka stora har utvecklat studier med tillämpningar med tillämpningar inom olika kunskapsområden.
Förklaring
För det första, för större komprimering av detta teorem, är vissa grundläggande uppfattningar om sannolikhetsteori nödvändig, särskilt multiplikationsteoremet för villkorad sannolikhet, vilket fastställer det
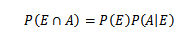
För E och till godtyckliga händelser i ett provutrymme.
Och definitionen av partitioner, som säger till oss att vi har1 ,TILL2,Till ..., tilln Händelser i ett provutrymme kommer dessa att bilda en partition av S, om aYo De är ömsesidigt exklusiva och deras fackförening är.
Kan tjäna dig: vad är siffrorna för? De 8 huvudanvändningarnaHar detta, vare sig det är en annan händelse. Så vi kan se B som
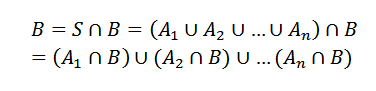
Där enYo korsade med B är ömsesidigt exklusiva händelser.
Och följaktligen,
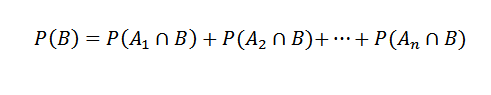
Sedan tillämpa multiplikationsteoremet
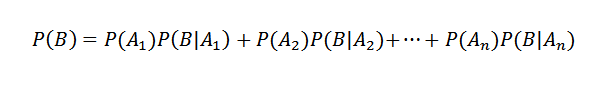
Å andra sidan definieras den villkorade sannolikheten för AI B av
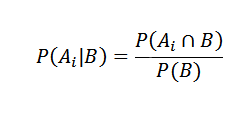
Ersätter ordentligt vi har det för alla i
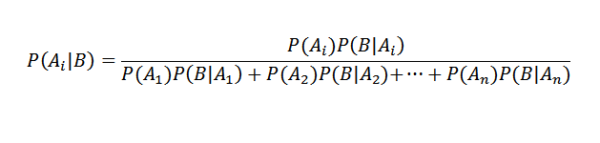
Bayes Theorem -applikationer
Tack vare detta resultat har forskningsgrupper och olika företag lyckats förbättra de system som är baserade på kunskap.
Sjukdomsstudie
I studien av sjukdomar kan till exempel Bayes teorem hjälpa till att urskilja sannolikheten för att en sjukdom kommer att hittas i en grupp människor med en given egenskap och ta som data de globala hastigheterna för sjukdomen och övervägande av nämnda egenskaper hos båda friska och sjuka människor.
Mjukvaruutveckling
Å andra sidan, i världen av hög teknik, har det påverkat stora företag som har utvecklats, tack vare detta resultat, programvara "baserad på kunskap".
Som ett dagligt exempel har vi Microsoft Office Assistant. Bayes 'Theorem hjälper programvara för att utvärdera de problem som användaren presenterar och bestämma vilka råd de ska ge och därmed kunna erbjuda en bättre service enligt användarens vanor.
Det bör noteras att denna formel ignorerades fram till senare tid, detta beror främst på att när detta resultat utvecklades för 200 år sedan var det lite praktiskt bruk för dem. Men i vår tid, tack vare de stora tekniska framstegen, har forskare uppnått sätt att utöva detta resultat i praktiken.
Löst övningar
Övning 1
Ett mobiltelefonföretag har två A- och B -maskiner. 54% av mobiltelefonerna tillverkas av maskin A och resten av maskin B. Inte alla mobiltelefoner är i gott skick.
Kan tjäna dig: faktoriseringAndelen defekta mobiltelefoner gjorda av A är 0.2 och för B är 0.5. Vad är sannolikheten för att en mobiltelefon till nämnda fabrik är defekt? Vad är sannolikheten för att veta att en mobiltelefon är defekt kommer från maskinen till?
Lösning
Här har du ett experiment som utförs i två delar; I den första delen inträffar händelserna:
Till: mobiltelefon tillverkad av maskin a.
B: Mobiltelefon tillverkad av maskin B.
Eftersom maskin A producerar 54% av mobiltelefonerna och resten produceras av maskin B, måste maskin B producera 46% av mobiltelefonerna. Chanserna för dessa händelser ges, nämligen:
P (A) = 0,54.
P (b) = 0,46.
Händelserna i den andra delen av experimentet är:
D: Defekt mobiltelefon.
E: icke -defektiv cell.
Som anges i uttalandet beror sannolikheterna för dessa händelser på resultatet som erhållits i den första delen:
P (d | a) = 0,2.
P (D | B) = 0,5.
Med hjälp av dessa värden kan du också bestämma sannolikheterna för tillbehören för dessa händelser, det vill säga:
P (E | A) = 1 - P (D | A)
= 1 - 0,2
= 0,8
och
P (E | B) = 1 - P (D | B)
= 1 - 0,5
= 0,5.
Nu kan D -händelsen skrivas enligt följande:
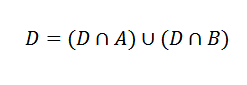 Dessa händelser är ömsesidigt exklusiva.
Dessa händelser är ömsesidigt exklusiva.
Att använda multiplikationsteoremet för villkorad sannolikhet är:
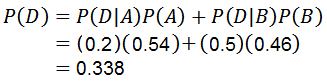
Med vilken den första frågan besvaras.
Nu behöver vi bara beräkna p (a | d), för vilken Bayes sats tillämpas:
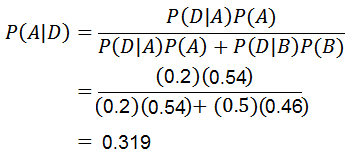
Tack vare Bayes teorem kan det bekräftas att sannolikheten för att en mobiltelefon har gjorts av maskin A, medveten om att mobiltelefonen är defekt, är 0.319.
Kan tjäna dig: icosagonoÖvning 2
Tre lådor innehåller svarta och svarta bollar. Kompositionen för var och en av dem är som följer: u1 = 3b, 1n, u2 = 2b, 2n, u3 = 1b, 3n.
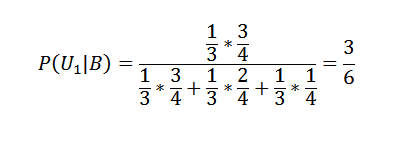
En slumpmässigt utvalda en av lådorna och en slumpmässig boll extraheras från den som visar sig vara vit. Vad är lådan med det mest troligt att de har valts?
Lösning
Genom U1, U2 och U3 kommer vi också att representera den valda rutan.
Dessa händelser utgör en partition av S och det verifieras att P (U1) = P (U2) = P (U3) = 1/3 eftersom valet av rutan är slumpmässigt.
Om B = den extraherade bollen är vit, kommer vi att ha P (B | U1) = 3/4, P (B | U2) = 2/4, P (B | U3) = 1/4 .
Vad vi vill få är sannolikheten för att bollen har tagits från iu -rutan med att veta att den här bollen var vit, det vill säga p (ui | b), och att se vilka av de tre värdena som var den högsta att veta vilken varav rutan har varit mer benägna att utvinas till den vita bollen.
Tillämpa Bayes teorem på den första av rutorna:
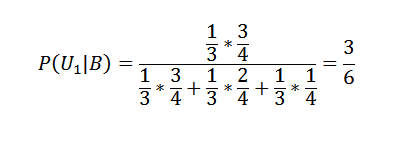
Och för de andra två:
P (U2 | B) = 2/6 och P (U3 | B) = 1/6.
Sedan är den första av lådorna den som har en större sannolikhet för att ha valts för utvinning av den vita bollen.