Thévenin teorem vad som består, applikationer och exempel

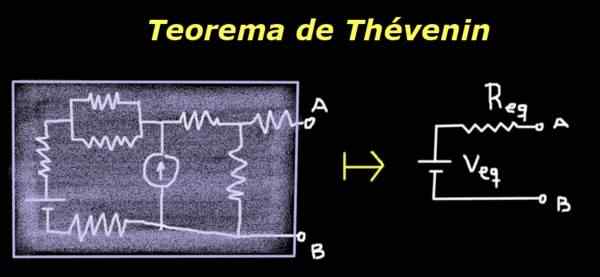
han Thévenin teorem Den säger att en krets med terminaler A och B kan ersättas av en motsvarande en som består av en källa och ett seriemotstånd, vars värden ger samma potentialskillnad mellan A och B och samma impedans som den ursprungliga kretsen.

Denna sats släpptes 1883 av den franska ingenjören Léon Charles Thévenin, men det hävdades att han uppgavs trettio år innan av den tyska fysikern Hermann von Helmholtz.

Figur 1. Thévenin teorem. Källa: Självgjord

Dess användbarhet ligger i det faktum att även om den ursprungliga kretsen är komplex eller okänd, för en belastning eller impedans som placeras mellan terminalerna A och B, uppför den enkla motsvarande kretsen för Thévenin på samma sätt som originalet.

[TOC]

Hur beräknas motsvarande spänning steg för steg?

Spänningen eller potentialskillnaden i motsvarande krets kan erhållas på följande sätt:

- Experimentellt

Erhålla motsvarande spänning av thévenin

Om det är en enhet eller utrustning som finns i en "svart låda" mäts potentialskillnaden mellan terminaler A och B med en voltmeter eller ett oscilloskop. Det är mycket viktigt att ingen belastning eller impedans mellan terminaler A och B placeras. 

En voltmeter eller ett oscilloskop representerar inte någon belastning för terminalerna, eftersom båda lagen har en mycket stor (idealiskt oändlig) impedans och skulle vara som om terminaler A och B var utan belastning. Spänningen eller spänningen som erhålls på detta sätt är motsvarande spänning i Thévenin.

Att få motsvarande impedans av Thévenin

För att erhålla motsvarande impedans från en experimentell mätning placeras ett motstånd som är känt mellan A- och B -terminalerna och spänningsfallet eller spänningssignalen med ett oscilloskop mäts. 

Från spänningsfallet i motståndet som är känt bland terminalerna kan strömmen som cirkulerar genom den erhållas. 

Produkten från strömmen erhållen med motsvarande motstånd plus den uppmätta spänningsfallet i det kända motståndet är lika med den motsvarande spänningen av thévenin som tidigare erhållits. Från denna jämlikhet rensas motsvarande impedans av thévenin.

- Lösa kretsen

Thévenins motsvarande spänningsberäkning

Först kopplas alla belastningar eller impedans av terminaler A och B.

Som kretsen är känd tillämpas meshes eller Kirchhoffs lagar för att hitta spänningen i terminalerna. Denna spänning kommer att vara Thévenins motsvarande.

Kan tjäna dig: Mount Olympus (Mars)

Thévenins motsvarande impedansberäkning

För att få motsvarande impedans fortsätter vi till:

- Byt ut de ursprungliga kretsspänningskällorna med korta kretsar "nollimpedans" och källorna till originalkretsen för öppen "oändlig impedans".

- Sedan beräknas motsvarande impedans efter reglerna för serieimpedans och impedanser parallellt.

Thévenin Theorem -applikationer (del I)

Vi kommer att tillämpa Thévenins sats för att lösa vissa kretsar. I den första delen överväger vi en krets som bara har spänningskällor och motstånd.

Exempel 1 (beräkning av motsvarande spänning steg för steg)

Figur 2 visar kretsen som finns i en himmelbox som har två batterier av elektromotorkraft V1 respektive V2 respektive motstånd R1 och R2, har kretsen terminaler A och B till vilka en belastning kan anslutas.

figur 2. Exempel 1 i Thévenin -satsen. Källa: Självgjord

Målet är att hitta den motsvarande kretsen i Thévenin, det vill säga bestämma VT- och RT -värdena för motsvarande krets.  Använd följande värden: V1 = 4V, V2 = 1V, R1 = 3Ω, R2 = 6Ω och R = 1Ω.

Steg för steg

Steg 1 

Vi kommer att bestämma spänningen i terminalerna A och B när de inte placeras någon belastning.

Steg 2

Kretsen som ska lösas består av ett enda nät genom vilket en ström jag cirkulerar som vi har tagit positivt på medurs.

Steg 3

Vi reser nätet börjar med det nedre vänstra hörnet. Rutten leder till följande ekvation:

V1 - i*r1 - i*r2 - v2 = 0

Steg 4

Vi rensar nätströmmen i och får:

I = (v1 -v2) / (r1 +r2) = (4V - 1V) / (3Ω +6Ω) = ⅓ a

Steg 5

Med nätströmmen kan vi bestämma spännings- eller spänningsskillnaden mellan A och B, vilket är:

VAB = V1 - I * R1 = 4V - ⅓ A * 3Ω = 3V

Det vill säga att Thevenins motsvarande spänning är: VT = 3V.

Steg 6 (Thévenin motsvarande motstånd)

Vi fortsätter nu med att beräkna Thévenins motsvarande motstånd, för vilket och som tidigare sagt, spänningskällor ersätts av en kabel.

I så fall har vi bara två motstånd parallellt, så Thévenins motsvarande motstånd är:

RT = (R1 * R2) / (R1 + R2) = (3Ω * 6Ω) / (3Ω + 6Ω) = 2Ω

Exempel 1B (strömström med théveninekvivalenten)

Anslut som last till terminaler A och B A Motstånd R = 1Ω till motsvarande krets och hitta strömmen som cirkulerar genom nämnda last. 

Kan tjäna dig: rätlinjig rörelse: egenskaper, typer och exempel

Lösning

När motståndet r är ansluten till den ekvivalenta kretsen i Thevenin finns det en enkel krets som består av en VT -källa ett seriemotstånd i serie med motstånd R. 

Vi kommer att kalla strömmen som cirkulerar genom belastningen R, så att nätekvationen är så här:

Vt - ic* rt - ic* r = 0

Från vilket det följer att IC ges av:

IC = VT / (RT + R) = 3V / (2Ω + 1Ω) = 1 A

Thévenin teorem verifiering

För att verifiera att Thévenins teorem är uppfyllt, ansluta R till den ursprungliga kretsen och hitta strömmen som cirkulerar genom att tillämpa lagen om mesh på den resulterande kretsen.

Den resulterande kretsen kvarstår och dess nätekvationer är som visas i följande figur:

Figur 3. Mesh -strömmar. (Egen utarbetande)

Att lägga till nätekvationerna är det möjligt att hitta nätströmmen i1 beroende på ström i2. Sedan ersätts den i den andra nätekvationen och det finns en ekvation med i2 som den enda okända. Följande tabell visar operationer.

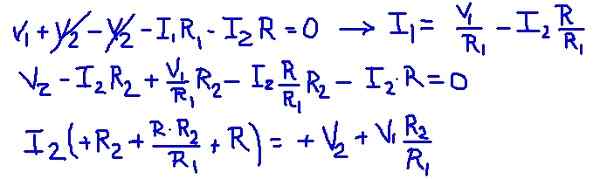Figur 4. Verksamhetsdetaljer. (Egen utarbetande)

Sedan ersätts motståndsvärdena och spänningarna på källorna, vilket erhåller det numeriska värdet på i2 -nätströmmen.

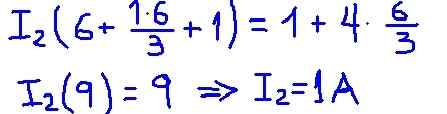Figur 5. Resultatdetalj. (Egen utarbetande)

I2 -nätströmmen är strömmen som cirkulerar genom lastmotståndet R och värdet som hittades från 1 A helt sammanfaller med det som tidigare hittades med motsvarande krets av Thévenin.

Tillämpning av Thévenins sats (del II)

I den andra delen kommer Thévenins sats till att tillämpas i en krets som har spänningskällor, nuvarande källa och motstånd. 

Exempel 2A (Thévenin motsvarande resistens)

Målet är att bestämma den ekvivalenta kretsen för Thévenin som motsvarar kretsen i följande figur, när terminalerna är utan motståndet hos 1 ohmio, sedan placeras motståndet och strömmen bestäms av samma.

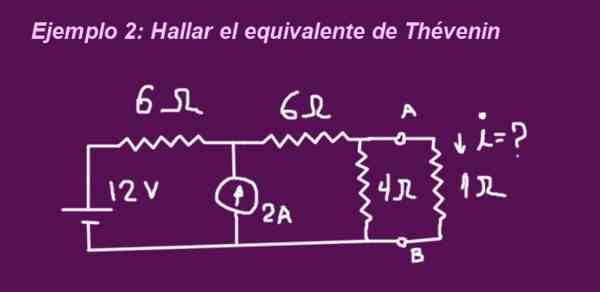Figur 6. Exempel 2 -krets. (Egen utarbetande)

Lösning

För att hitta motsvarande motstånd avlägsnas belastningsmotståndet (i detta fall det för 1 ohmio). Dessutom ersätts spänningskällor av en kortslutning och nuvarande källor med en öppen krets. 

På detta sätt är den krets som motsvarande motstånd kommer att beräknas nedan:

Kan tjäna dig: Boltzmann Constant: Historia, Ekvationer, beräkning, övningar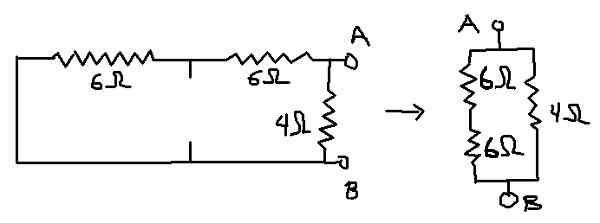Figur 7. Detalj för beräkning av motsvarande motstånd (egen utarbetande)

Rab = (12Ω * 4Ω) / (12Ω + 4Ω) = 3Ω, vilket är motsvarande resistens av thevenin (RTH).

Exempel 2b 

Beräkna Thévenins motsvarande spänning.

Lösning

För att beräkna motsvarande spänning av Thévenin överväger vi följande krets, där vi kommer att placera strömmarna i I1 och I2 i de grenar som anges i följande figur:

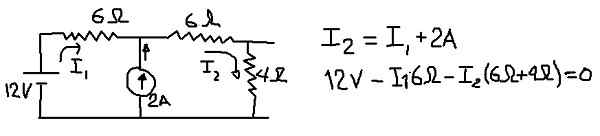Figur 8. Detaljer för beräkning av Thévenins spänning. (Egen utarbetande)

I den föregående figuren visas ekvationen för de aktuella noderna och spänningsekvationen när det externa nätet resas. Från den andra av ekvationerna rensas strömmen i1:

I1 = 2 - i2*(5/3)

Denna ekvation ersätts i noderekvationen:

I2 = 2 - (5/3) i2 + 2 ===> i2 (8/3) = 4 ===> i2 = 12/8 = 1,5 a

Detta innebär att spänningen minskar 4 ohm -motståndet är 6 volt.

Kort sagt, Thévenins spänning är VTH = 6 V.

Exempel 2C

Hitta den motsvarande kretsen för thevenin och ström i lastmotståndet.

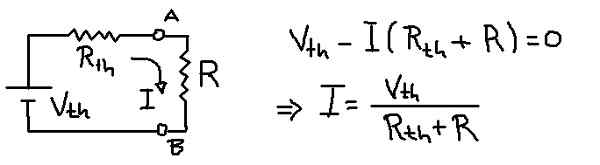Figur 9. Aktuell i belastning med Thévenin -ekvivalent. (Egen utarbetande)

Lösning

Den föregående siffran visar den motsvarande kretsen för thévenin med lastmotståndet r. Från spänningsekvationen i nätet dras den strömmen som cirkulerar genom belastningsmotståndet.

I = vth / (rth + r) = 6V / (3Ω + 1Ω) = 1,5 a

Tillämpning av Thévenins sats (del III)

I denna tredje del av Thévenins satsapplikation innehåller en växelströmskrets en växelkälla, en kondensor, induktans och motstånd övervägs. 

Exempel 3

Målet är att hitta den motsvarande Thévenin -kretsen för följande krets:

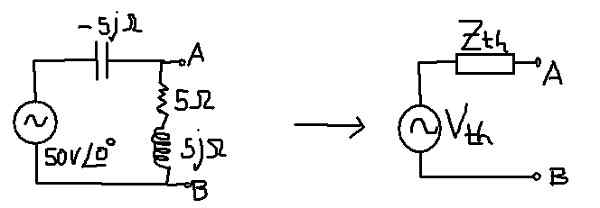Figur 10. Thévenin i en växlande strömkrets. (Egen utarbetande)

Lösning

Motsvarande impedans motsvarar kondensorns parallellt med motstånds- och induktansseriekombinationen.

Den inversa av motsvarande impedans ges av:

Zeq^-1 = (-5j)^-1 + (5 + 5J)^-1 = (1/5) J + ((1/10 + (1/10) J) = (1/10 + 3/ 10 j) MHO

Och motsvarande impedans kommer då att vara:

Zeq = (1 - 3 j) ohm

Den komplexa strömmen kan jag härledas från nätekvationen:

50Viera0 - i (-5 j + 5 + 5j) = 50Vräv0 - i*5 = 0 ===> i = 10a ∠0 

Nu beräknas spänningsfallet i motstånd plus induktans, det vill säga VAB -spänningen som kommer att vara motsvarande spänning i Thévenin:

VAB = I * (5 + 5 J) Ω = 10A ∠0 * 5Ωigur

Med andra ord

Referenser

1. Elektronikhandledning, TheVevenins teorem. Återhämtat sig från: elektronik-mormaler.Ws
2. Nätverksteorifrågor och svar. Thevenins teorem. Återhämtat sig från: Sanfoundry.com
3. Thevenins teorem. Steg för steg. Återhämtat sig från: elektricteknik.org
4. Thevenins teorem. Löst exempel steg för steg. Hämtad från: ElecticalSimple.Bloggfläck.com
5. Workshop på TheVevenins och Nortons teorems. Hämtad från: webben.jag det.Edu
6. Wikipedia. Thévenin teorem. Återhämtat sig från: Wikipedia.com