Varignonsteorem

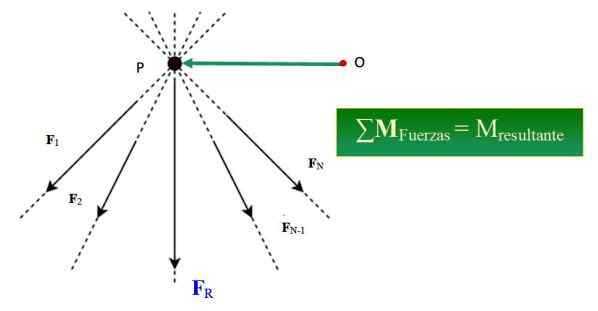
Figur 1.- Varignons sats bekräftar att summan av styrkornas ögonblick runt en viss punkt motsvarar resultatet med avseende på den punkten. Källa: Wikimedia Commons/F. Zapata.

Vad är Varignons teorem?

Varignons teorem, i mekanik, säger att summan av de ögonblick som produceras av ett system med samtidiga krafter med avseende på en viss punkt, är lika med den resulterande kraftens ögonblick med avseende på samma punkt.

Av denna anledning är detta teorem också känt som Början av ögonblicken.

Medan den första som uppger att det var holländaren Simon Stevin (1548-1620), var skaparen av den hydrostatiska paradoxen, den franska matematikern Pierre Varignon (1654-1722) den som därefter gav honom sin definitiva form.

Ett exempel på hur Varignons sats fungerar i mekanik är som följer: Anta att ett enkelt system med två coplanarer och samtidiga krafter verkar på en punkt F₁ och F₂, (Betecknad med djärv för sin vektorkaraktär). Dessa krafter ger upphov till ett nät eller resulterande kraft, kallad F_R.

Varje kraft utövar ett vridmoment eller ett ögonblick med avseende på en punkt eller, som beräknas av vektorprodukten mellan positionsvektorn r_Op och strengh F, var r_Op Det är riktat från eller till punkten för samtidighet P:

M_O1 = r_Op × F₁

M_O2 = r_Op × F₂

Med tanke på F_R = F₁ + F₂, så:

M_ANTINGEN = r_Op × F₁ + r_Op × F₂ = M_O1 + M_O2

Men hur r_Op Det är en vanlig faktor att tillämpa distribuerande egendom på tvärprodukten:

M_ANTINGEN = r_Op × (F₁ + F₂) = r_Op × F_R                

Därför är summan av stunder eller moment för varje kraft med avseende på punkten eller motsvarar tiden för den resulterande kraften med avseende på samma punkt.

Uttalande och demonstration

Vara ett system med n samtidiga krafter, bildade av F₁, F₂, F₃.. F_N, vars handlingslinjer är avsedda vid punkt P (se figur 1), ögonblicket för detta kraftsystem M_ANTINGEN, Angående en punkt eller ges av:

Kan tjäna dig: instabil balans: koncept och exempel

M_ANTINGEN = r_Op × F₁ + r_Op × F₂ + r_Op × F₃ +.. r_Op × F_N = r_Op × (F₁ + F₂ + F₃ +.. F_N)

Demonstration

För att demonstrera satsen görs vektorproduktens distributiva egenskap mellan vektorerna.

Vara krafterna F₁, F₂, F₃.. F_N tillämpas på poäng på₁, TILL₂, TILL₃Till ... till_N och samtidig vid punkt P. Det resulterande ögonblicket för detta system, med avseende på en punkt eller kallas M_ANTINGEN, Det är summan av stunderna för varje styrka, med avseende på den punkten:

M_ANTINGEN = ∑ r_Oai × F_Yo

Där summan går från i = 1 till i = n, eftersom det finns n krafter. Eftersom dessa är samtidiga krafter och eftersom vektorprodukten mellan parallella vektorer är noll, händer det att:

r_Pai × F_Yo = 0

Med nollvektorn som betecknas som 0.

Ögonblicket för en av krafterna angående O, till exempel kraften F_Yo appliceras i en_Yo, Det är skrivet så här:

M_{Jag hörde} = r_Oai × F_Yo

Positionsvektorn r_Oai  Det kan uttryckas som summan av två vektorer position:

r_Oai = r_Op + r_Pai

På detta sätt, ögonblicket med avseende på eller kraft F_Yo är:

M_{Jag hörde} = (r_Op + r_Pai× F_Yo = (r_Op × F_Yo) + (r_Pai × F_Yo)

Men den sista terminen är noll, som förklarats ovan, för r_Pai är på väg att handla om F_Yo, därför:

M_{Jag hörde} = r_Op × F_Yo

Att veta att systemets ögonblick med avseende på punkt eller är summan av alla enskilda stunder för varje styrka med avseende på den punkten, då:

M_ANTINGEN = ∑ M_{Jag hörde} = ∑ r_Op × F_Yo

Som r_Op Det är konstant kommer ut ur summan:

M_ANTINGEN = r_Op × (∑ F_Yo)

Men ∑ F_Yo Det är helt enkelt det resulterande nätet eller kraften F_R, Därför dras det omedelbart till att:

Kan tjäna dig: Leyden -flaska: delar, drift, experiment

M_ANTINGEN = r_Op × F_R

Exempel

Varignons sats underlättar beräkningen av kraften i styrkan F Beträffande punkten eller strukturen som visas i figuren, om kraften bryts ned i dess rektangulära komponenter och ögonblicket för var och en av dem beräknas:

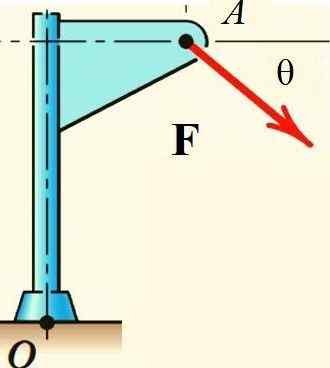figur 2.- Varignons sats gäller för att beräkna kraftmomentet runt eller. Källa: f. Zapata.

Varignon Theorem -applikationer

När kraften som härrör från ett system är känt kan Varignons teorem tillämpas för att ersätta summan av vart och ett av de ögonblick som produceras av de krafter som komponerar det vid resulterande tidpunkt.

Om systemet består av krafter på samma plan och punkten med avseende på vilket du vill beräkna ögonblicket tillhör det planet, är det resulterande ögonblicket vinkelrätt.

Till exempel, om alla krafter är i XY -planet, riktas ögonblicket på Z -axeln och återstår bara att hitta dess storlek och dess betydelse, så är fallet med exemplet som beskrivs ovan.

I så fall tillåter Varignons sats att beräkna det ögonblick som härrör från systemet genom summeringen. Det är mycket användbart i fallet med ett system med tre dimensionella krafter, för vilka riktningen för det resulterande ögonblicket inte är känt a priori.

För att lösa dessa övningar är det bekvämt.

Träning löst

Beräkna kraften F runt punkten eller visas i figuren om varignons teorem.

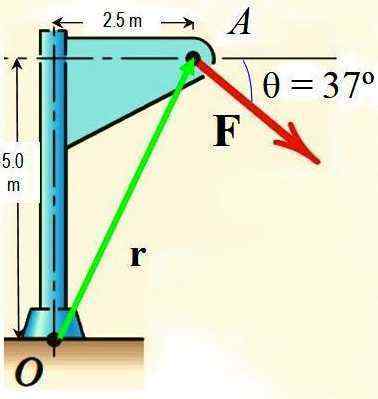Figur 3.- Figur för den löst som lösts. Källa: f. Zapata.

Lösning

För att tillämpa Varignons teorem sönderdelas Force F i två komponenter, vars respektive stunder runt eller beräknas och läggs till för att få det resulterande ögonblicket.

Kan tjäna dig: styv kropp

F_x = 725 n ∙ cos 37 º = 579.0 n

F_och = - 725 n n ∙ Sen 37 º = −436.3 n

På liknande sätt positionsvektorn r riktad från eller till A har komponenterna:

r_x = 2.5 m

r_och = 5.0 m

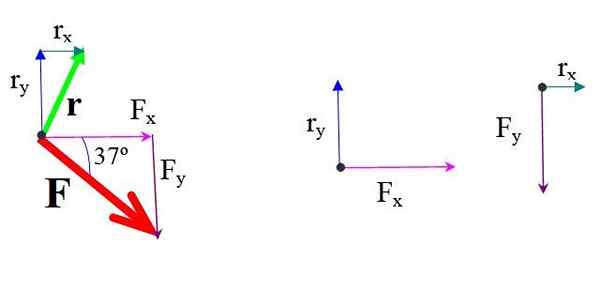Figur 4.- Kraft- och positionskomponenter. Källa: f. Zapata.

Momentet för varje komponent i kraften med avseende på eller multiplicerar kraften och vinkelrätt avstånd.

Båda krafterna tenderar att rotera strukturen i samma riktning, som i detta fall är poängkänslan, som godtyckligt tilldelas positivt tecken:

M_Oxe = F_x∙ r_och ∙ Sin 90º = 579.0 n ∙ 5.0 m = 2895 n ∙ m

M_Oy = F_och∙ r_x ∙ sin (−90º) = −436.3 n ∙ 2.5 m ∙ (−1) = 1090.8 n ∙ m

Det resulterande ögonblicket med avseende på eller är:

M_ANTINGEN = M_Oxe + M_Oy = 3985.8 n ∙ m vinkelrätt mot planet och i ett vridmoment.

Referenser

1. Bedford, 2000. TILL. Mekanik för teknik: statisk. Addison Wesley. 
2. Öl, f. 2010. Statisk. McGraw Hill. 9na. Utgåva.
3. Hibbeler, R. 1992. Mekanik för ingenjörer. Sjätte. Utgåva. CECSA.
4. HK -teknik. Varignonsteorem. Återhämtat sig från: YouTube.com.
5. Wikipedia. Varignons sats (mekanik). Hämtad från: i.Wikipedia.org.