Typer av trianglar

Klassificering av trianglar

En triangel är en polygon eller geometrisk figur som har tre sidor, tre vertikaler och tre vinklar. Sidorna är var och en av de raka linjerna som bildar den. Virtarna är de punkter där sidorna är förenade; Vinklarna är bågarna eller öppningarna som bildas nära topparna genom att gå med två sidor.

En triangel kan också definieras som området som bestäms av tre linjer. Summan av dess tre vinklar är alltid lika med 180º. Längden på någon av dess sidor är alltid mindre än resultatet av summan av längden på de andra två sidorna, men större än dess subtraktion.

Trianglar är de enklaste geometriska figurerna och tjänar till att undersöka de matematiska egenskaperna hos andra mer komplexa figurer, såsom pentagoner eller hexagoner.

De används också inom andra vetenskaper, såsom topografi, navigering eller astronomi. I det senare används de för att veta avståndet som skiljer oss från en avlägsen ljusblå kropp från två observationspunkter som ligger på jorden. Denna metod kallas parallage.

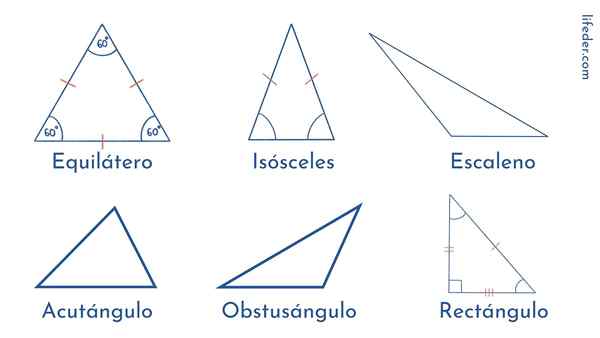
Trianglarna klassificeras beroende på längden på deras sidor eller enligt amplituden på deras vinklar.

Typer av trianglar enligt deras sidor

Liksidig triangel

Sidorna på denna typ av triangel har exakt samma längd. Och detsamma gäller för deras vinklar: de tre mäter 60º. Det är därför vi säger att den liksidiga triangeln är en vanlig polygon.

Skalen triangel

Till skillnad från de liksidiga, i skalen triangeln är allt ojämlikt: dess tre sidor har olika längder och dess vinklar skiljer sig åt i amplitud.

Kan tjäna dig: kombinerade operationer

Likbent triangel

I denna typ av triangel finner vi att två sidor har samma mått, medan den återstående sidan är annorlunda. Detsamma observeras i vinklens amplitud: två är desamma och en annorlunda.

Typer av trianglar enligt deras vinklar

Höger triangel

Det kännetecknas av att ha rätt vinkel, det vill säga 90º. Hans andra två vinklar är akuta eller mindre än 90º.

I denna typ av trianglar kallas den längsta sidan hypotenusa, medan ytterligare två sidor är kategorierna.

Sned triangel

Trianglar som inte har någon rätt vinkel tillhör den här typen. De är indelade i två typer:

Acutangle triangel: Hans tre vinklar är akuta.

Triangel: de har två akuta vinklar och en otrevlig eller större än 90º.

Blandade trianglar

Samma triangel kan klassificeras enligt de två kriterierna, det vill säga enligt deras sidans längd och deras vinklar amplitud.

Till exempel kan en rektangel triangel också vara escalano eller isosceles, men det kunde inte vara liksidigt, eftersom den senare inte presenterar någon rätt vinkel.

Emellertid kan en liksidig triangel vara akut, eftersom den effektivt har tre akuta eller mindre än 90 ° vinklar.

Triangel

En skala triangel kan vara otydligt, eftersom både amplituden på dess vinklar och dess sidor är olika.

Hur man beräknar omkretsen av en triangel?

Produkten av summan av längden på de tre sidorna på en triangel kallas omkrets.

Låt oss titta på några exempel.

1- Vi uppmanas att hitta omkretsen av en skalen triangel vars sidor 6, 8 och 4 centimeter. Allt vi behöver göra är att lägga till:

Kan tjäna dig: absolut konstant

6 + 8 + 4 = 18

Därför är omkretsen av denna skalen triangel 10 centimeter.

2- Då ber de oss att beräkna omkretsen av en isosceles triangel vars sidor mäter 4 centimeter de två och 6 centimeter den återstående sidan. Eftersom två av dess sidor har samma längd måste vi placera samma figur två gånger, så här:

4 + 4 + 6 = 14

Omkretsen av denna triangel är 14 centimeter.

3- Ett sista exempel. Vi har uppgiften att bestämma omkretsen av en liksidig triangel på 9 centimeter i sidled. Som vi vet egenskaperna hos de olika typerna av trianglar, vet vi att jämlikheten är utmärkt eftersom dess tre sidor är lika. Därför:

9 + 9 + 9 = 27

Omkretsen av denna liksidiga är 27 centimeter.

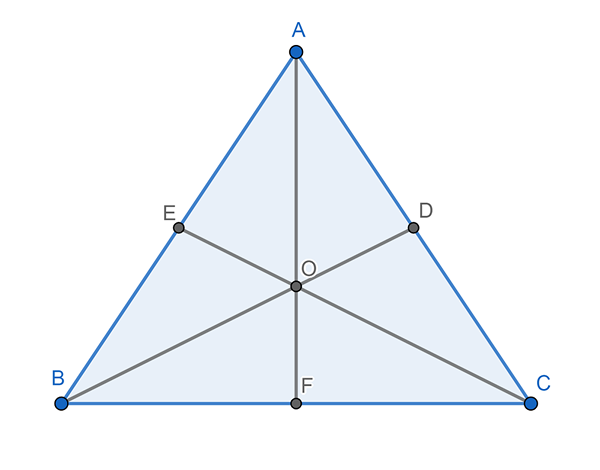
Mediatrices, bisektorer och medium

Det här är de tre typerna av raka linjer som kan dras i en triangel.

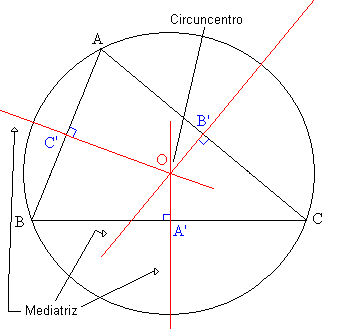
Mediatricer

Det finns tre, en på varje sida av triangeln. MediaTrix är en rak linje som passerar genom mittpunkten på triangelsidan som den motsvarar. De tre medier av en triangel korsar vid en punkt som kallas Circumcentro, som ligger på samma avstånd från var och en av triangelns toppar.

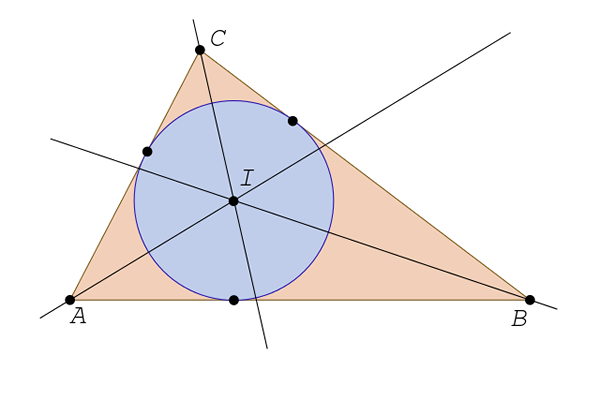
Bisektorer

Det finns tre, en för varje vinkel. Bisektorn är en rak linje som startar från toppunkten och delar vinkeln i två lika delar. Bisektorerna i en triangel korsar varandra vid en punkt som kallas incitret.

Medium

Det finns också tre, en för varje toppunkt. En median är en linje som startar från ett toppunkt och når mittpunkten på motsatt sida. Medianerna i en triangel korsar varandra vid en punkt som kallas baricentro.

Kan tjäna dig: provtagningsfel: formler och ekvationer, beräkning, exempel

Avståndet mellan någon av de tre vertikalerna och BaryCenter motsvarar två tredjedelar (2/3) av den totala längden på motsvarande median. Till exempel, om median CE mäter 5 centimeter, är avståndet mellan C och baricenter (O) lika med 5 x 2/3, eller vad som är detsamma, 5 x 0,66, vilket resulterar i 3, 3 centimeter.

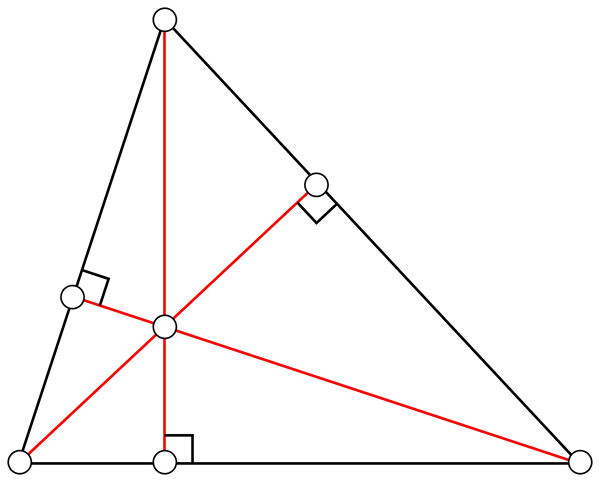
Höjder

Det är en rak linje som ansluter sig till ett toppunkt med motsatt sida. De tre höjderna på en triangel korsar varandra vid en punkt som kallas ortoenter. Beroende på typen av triangel kan ortocentret vara inom eller utanför triangelområdet.

Hur man beräknar triangelområdet?

Området för en triangel av något slag kan kännas när du tillämpar följande formel:

A = b x h / 2

I denna ekvation hänvisar A till området; B hänvisar till basen och h är höjden.

Låt oss titta på ett exempel. Vi uppmanas att beräkna området för en triangel vars bas mäter 12 centimeter och vars höjd är 7 centimeter. Således har vi:

B = 12

H = 7

Vi tillämpar formeln:

A = 12 x 7/2

A = 84/2

A = 44

Denna triangel har därför ett område på 44 kvadratcentimeter.