Triangel

Vi förklarar vad en stöt triangel är, dess element, egenskaper, typer, exempel och en upplöst övning

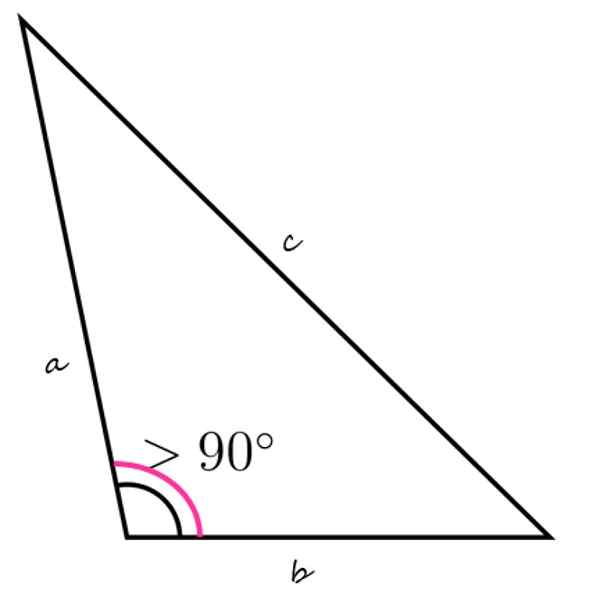Den stöt triangeln kännetecknas av att ha en inre vinkel större än 90º

Vad är en stöt triangel?

En triangel Det är den platta figuren, stängd och med tre sidor, som också innehåller en stöt inre vinkel, det vill säga större än 90º och mindre än 180 °.

Varje triangel innehåller 3 inre vinklar, och om en av dem är stöt, är de andra två, med kraft, akut, eftersom summan av de inre vinklarna i någon triangel alltid är lika med 180º.

Den översta figuren visar ett exempel på en stöt triangel, med den nedre vänstra inre vinkeln större än 90º. De återstående inre vinklarna måste lägga till mindre än 90º, bara på detta sätt är det sant att summan av de tre är lika med 180º.

Förutom de stötta trianglarna finns det akutangulösa trianglar, om alla dess inre vinklar är akuta och rektangel trianglar, när en av de inre vinklarna mäter exakt 90º.

Element i stöt trianglarna

Obtusángulos trianglar har de vanliga elementen till alla trianglar: de är 3 -sidiga platta figurer, med 3 inre vinklar och 3 vertikaler. Dessutom har de anmärkningsvärda segment, kallade Cevians, som höjd, median och mediatrix och punkter där Cevians korsar varandra.

Var och en av dessa element definieras kort på följande sätt:

-Sidor, är de segment som utgör figuren.

-Häckar, korsningspunkter för varje par angränsande sidor.

-Inre vinklar, De är mellan två angränsande sidor, på figurens inre sida, och sammanfaller vinkeln med toppen av triangeln.

-Yttre vinklar, De är mellan ena sidan och förlängningen av den angränsande sidan, utanför figuren, varav toppen är vanlig, både triangeln och vinkeln. Summan av måtten mellan den inre vinkeln och dess yttre angränsande vinkel är 180º, så att de är komplementära vinklar.

Det kan tjäna dig: Tukey Test: Vad är, vid exempel, löste träning

-Höjd, Det är måtten på det vinkelräta segmentet som förenar sig med ett toppunkt med motsatt sida eller med förlängningen av detta.

-Median, linje som är riktad från ett toppunkt till mitten av motsatt sida.

-Mediatrix, segment vinkelrätt mot sidan och det passerar precis genom dess centrum.

-Bisektris, Det är ett segment som delar sig i en halv inre vinkel i triangeln.

-Orocentro, korsningspunkten för de tre höjderna.

-Barycenter, Även kallad Centroid, det är punkten där de tre medianerna korsar varandra.

-Circumcentro, Här klipps de tre mediarerna.

-Incentrera, bisektorer.

När dessa koncept har granskats beskrivs några av de mest anmärkningsvärda egenskaperna hos de stötta trianglarna nedan.

Egenskaper

1.- Summan av de tre inre vinklarna i den stöt triangeln är 180º, därför kan endast en av dess inre vinklar vara större än 90º, medan summan av de återstående två är mindre än 90º.

2.- Den längsta sidan av den stöt triangeln motsätter sig den stöt vinkeln.

3.- I en stöt triangel, höjderna från topparna som gör akut vinkel, korsar tillägg på motsatta sidor.

4.- Ortocentret av en stöt triangel är ur figuren.

5.- Circumcentro of the Oantuse Triangle faller också ut ur triangeln (detta händer inte med Acutangle Triangle).

6.- Det är bara möjligt att registrera en fyrkant i den stöt triangeln, som stöder en av sidorna på torget på triangelns längsta sida. Två rutor kan ritas och stödja sidan på de kortaste sidorna av triangeln, vilket lämnar ett toppunkt som inte är registrerat (som inte rör vid triangelns sida).

Kan tjäna dig: tidecágono

7.- Vara en stöt triangel av sidor (a, b, c), som är c ​​den längsta sidan. Följande ojämlikhet är giltig:

till²+b² < c²

8.- De är två stötta trianglar, vars respektive sidor är (a, b, c) och (u, v, w). De längsta sidorna för var och en är C och W, så följande ojämlikhet uppfylls:

A ∙ u + b ∙ v < c∙w

Typer av hindrande trianglar

De stötta trianglarna kan vara av två typer, beroende på längden på deras sidor:

• Likbent
• Skala

De beskrivs kort nedan:

Likbent triangel

Det är en som har två lika sidor och en annan, det vill säga dess sidor är (a, a, c).

När Isosceles triangel är båda stöt, är sidorna av måtten "a" kortare och "c" -sidan är den längsta. Den stötvinkeln bildas mellan samma sidor, medan de två akuta vinklarna är av lika mått och bildas mellan sidorna "A" och sidan "C".

Och som anges i föregående avsnitt, sida "C", eftersom det är den längsta, det motsätter sig den stöt vinkeln.

Skalen triangel

De tre sidorna av skalen triangeln har olika mått: (a, b, c).

Exempel

Exempel 1

Triangeln som visas i följande figur är stöt. Stötvinkeln är γ = 114.5: e och det verifieras att summan av de tre inre vinklarna är 180º:

114.5: e + 36.8º + 28.6: e ≈ 180º

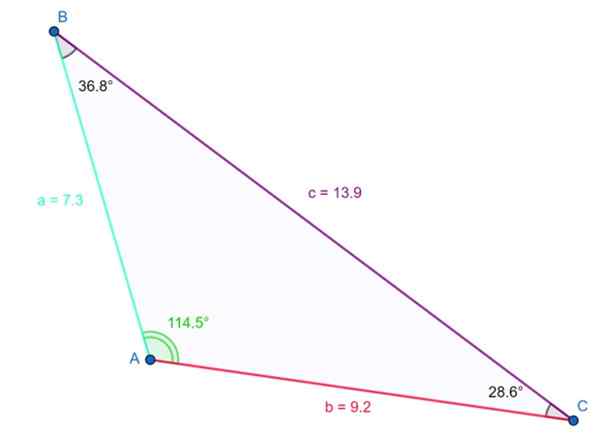Exempel på stöt triangel. Källa: f. Zapata

De längsta sidoåtgärderna 13.9 enheter och motsätter sig stötvinkeln. Den ovannämnda ojämlikheten uppfylls också:

till²+b² < c²

Kan tjäna dig: proportionalitetsrelationer: koncept, exempel och övningar

Ja a = 7.3 och B = 9.2, då:

7.3² + 9.2² < 13.9²

137.93 < 193.2

Exempel 2

I Calabi -triangeln är det möjligt att placera största möjliga torget, på tre olika sätt inom triangeln, som visas i följande figur.

Calabis triangel är liksikt och stöt. Den stöt vinkeln är ungefär 101.736 ° och akuta vinklar vid basen mäter båda 39.13: e, också ungefär.

Träning löst

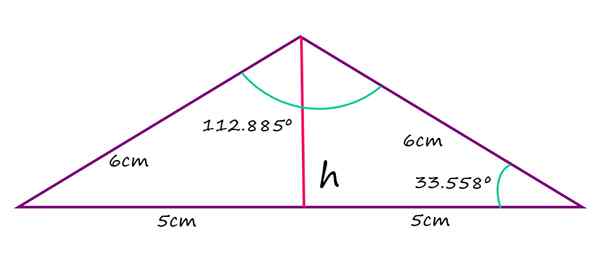
De lika sidorna av en stöt liksiktning triangel mäter 6 cm, medan den längsta sidan mäter 10 cm. Beräkna värdet på stötvinkeln, det för de återstående agudosvinklarna och höjden från nämnda toppunkt till basen.

Lösning

Cosine Theorem kan användas för att hitta kosinus i den stöt vinkeln. Sedan, med hjälp av kalkylatorn, bestäms vinkeln i fråga, betecknas som y.

Cosenos teorem säger att:

c² = a² +b² - 2ab ∙ cos y

Där y är vinkeln mellan sidorna a och b. Eftersom triangeln är isosceler är sidor A och B därför desamma:

c² = 2a² - 2: a²∙ cos y

Rensa cos γ:

 Den stöt vinkeln är -0 kosinusbågen.38889, som är ungefär 112.885º. Värdet på a, den akuta vinkeln som bildas av 6 cm sidor med 10 cm är:

2a + 112.885º = 180º

α = (180 - 112.885)/2 = 33.558º

Isosceles stöt triangel. Källa: f. Zapata

När det gäller höjden på triangeln, mätt från basen, erhålls den genom att observera att denna höjd delar upp triangeln i två lika rektanglar, med hypotenusa lika med 6 cm och bas 5 cm. I ett sådant fall gäller Pythagoras teorem för att direkt hitta värdet på H: