Balancer vektorberäkning, exempel, övningar

han balanseringsvektor Det är den som kontrasterar den resulterande vektorn och därför kan den balansera ett system, eftersom det har samma storlek och samma riktning, men i motsats till detta.

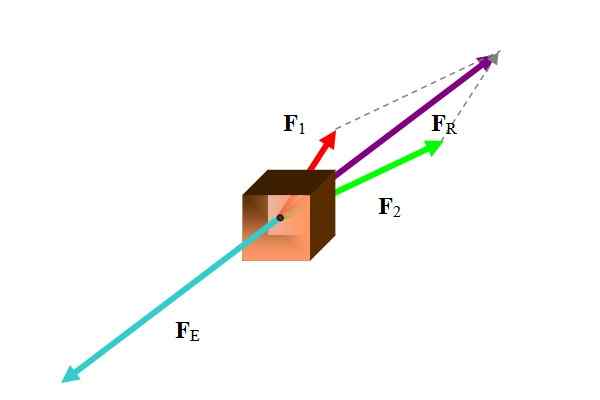
Vid flera tillfällen hänvisar balansvektorn till en kraftvektor. För att beräkna balanskraften är den resulterande kraften först, som visas i följande figur:

Figur 1. På en kropp två krafter lag vars resulterande är balanserad med kraft i turkosa färg. Källa: Självgjord.

Det finns olika metoder för att utföra denna uppgift, enligt uppgifterna. Eftersom krafterna är vektorer är resultatet vektorsumman av de deltagande krafterna:

F_R = F₁ + F₂ + F₃ +  .. .

Bland de metoder som ska användas är grafiska metoder såsom polygonala, parallellogram och analysmetoder såsom nedbrytning av krafter i deras kartesiska komponenter. I exemplet användes figuren parallellogrammetoden.

När den resulterande kraften har hittats är balansstyrkan just den motsatta vektorn.

Ja F_OCH Det är balansstyrkan, då uppfylls det F_OCH Tillämpas vid en viss punkt, det garanterar saldot i systemöversättningen. Om det är en enda partikel kommer den inte att röra sig (eller kanske det gör det med konstant hastighet), men om det är ett utökat objekt kommer det fortfarande att ha möjlighet att vända:

F_R + F_OCH = 0

[TOC]

Exempel

Balanskrafterna finns på alla sidor. Vi själva är balanserade av den kraft som stolen utövar för att kompensera för vikten. De föremål som finns i vila: böcker, möbler, taklampor och ett stort antal mekanismer, balanseras kontinuerligt av krafter.

Kan tjäna dig: inelastiska chocker: i en dimension och exempel

Till exempel balanseras en REST -bok på ett bord av den normala kraften som den utövar på boken och förhindrar att den faller. Detsamma gäller för kedjan eller kabeln som håller lampan som hänger i taket i ett rum. Kablarna som håller en belastning fördelas sin vikt genom spänningen i dem.

I en vätska kan vissa föremål flyta och förbli i vila, eftersom deras vikt balanseras av en stigande kraft som utövas av vätskan, kallad skjuta på.

Olika mekanismer måste vara balanserade med att känna till balansvektorn som staplar, balkar och kolumner.

När du använder en balans är det nödvändigt att på något sätt balansera vikten på objektet med en kraft som är motsvarande, antingen att lägga till vikter eller med fjädrar.

Kraftbord

Krafttabellen används i laboratoriet för att bestämma den balanserade kraften. Den består av en cirkulär plattform, av vilken du har den övre vyn i figuren, och som har en transportör för att mäta vinklar.

I bordets kanter finns det remskivor genom vilka strängar som håller vikter och som konvergerar i en båge som är i mitten.

Till exempel hängs två vikter. De spänningar som genereras på strängarna av dessa vikter dras i rött och blått i figur 2. En tredje väger grönt, kan balansera den andra två resulterande kraften och hålla systemet i balans.

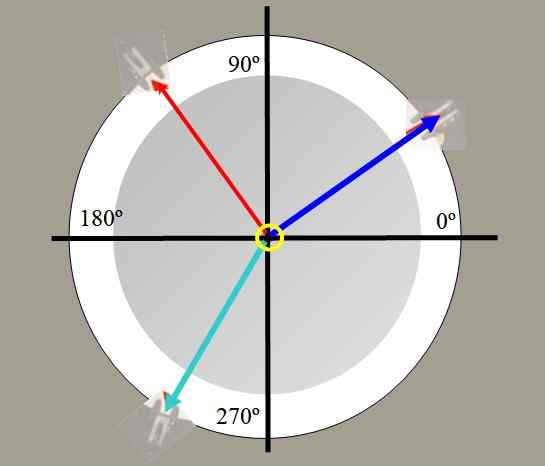figur 2. Utsikt från toppen av styrkorna. Källa: Självgjord.

Med krafttabellen kan du verifiera kraftens vektorkaraktär, sönderdela krafter, hitta balansstyrkan och verifiera Lamys sats:

Kan tjäna dig: sol

Om en Kroppen är i jämvikt tack vare tre coplanar, samtidiga och icke -kolineala (icke -parallella) krafter, kallade TILL, B och C, Förhållandet mellan dessa krafter är som följer:

A/ sin α = b/ Sen β = c/ Sen y

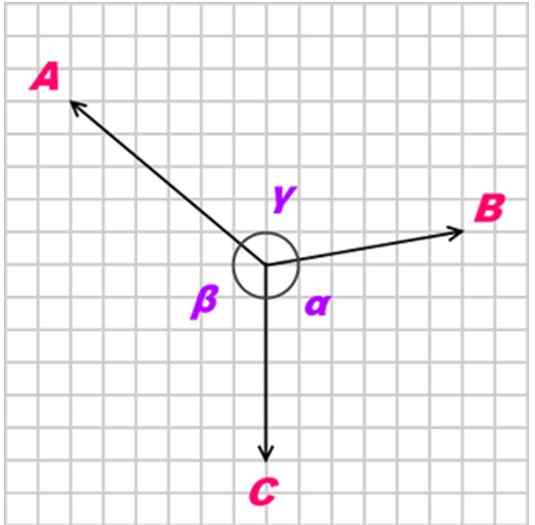Figur 3. Lamys sats gäller för samtidiga och coplanära styrkor. Källa: Wikimedia Commons.

Löst övningar

-Övning 1

I krafterna hängs tabellen i figur 2 på 225 g (blå spänning) och 150 g (röd spänning), med de visade vinklarna. Hitta värdet på balanskraften och vinkeln som denna form med den vertikala axeln.

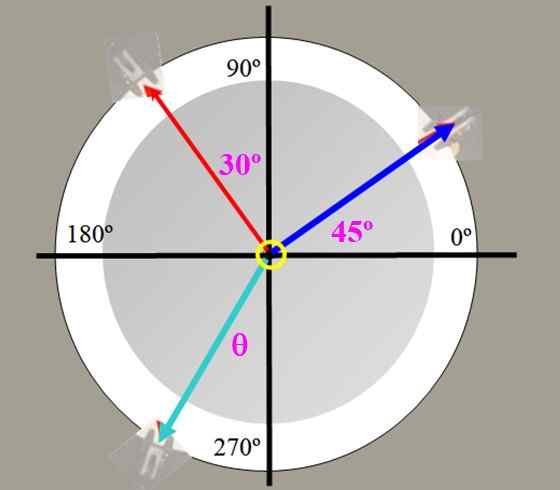Figur 4. Kraftbord för övning 1.

Lösning

Problemet kan arbetas med vikterna uttryckta i gram (krafter). Låt P₁ = 150 gram och p₂ = 225 gram, de respektive komponenterna i var och en är:

P_1x = 225 . COS 45º G = 159.10 g; P_1y = 225 . COS 45º G = 159.10 g

P_2x = -150 . Sen 30º g = -75.00 g; P_{2 och} = 150 . Cos 30º g = 129.90 g

Den resulterande vikten P_R Komponenterna är algebraiskt tillägg:

P_Rx = 159.10 - 75.00 g = 84.10 g

P_Ry = 159.10 + 129.90 g = 289.00 g

Balanseringsvikten P_OCH är motsatt vektor P_R:

P_Ex = -84.10 g

P_Hallå = -289.00 g

Storleken på balanseringsvikten beräknas av:

P_OCH = (P_Ex² + P_Hallå²)^1/2 = ((-84.10)² + (-289.00)²)^1/2 G = 301 g

Figurens vinkel θ är:

θ = arctg (-84.10 / -289.00) = 16.2: a med avseende på axeln och negativ.

-Övning 2

Hitta balansvektorn i systemet som visas i figuren, och vet att varje kvadrat mäter 10 m sida.

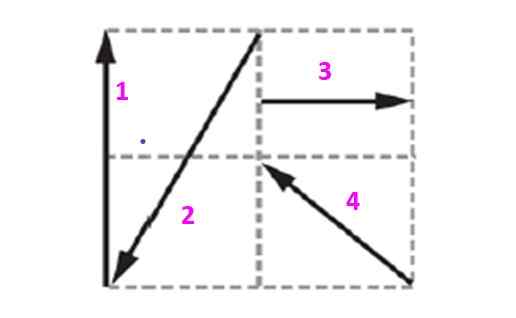Figur 5. Diagram för exemplet löst 2.

Lösning

Vektorerna i detta rutnät kommer att uttryckas i termer av enheten och ortogonala vektorer Yo och J som bestämmer planet. Vektor 1, som kommer att betecknas som v₁ Den har 20 m storlek och riktas vertikalt uppåt. Det kan uttryckas som:

Det kan tjäna dig: strålningsvärmeöverföring (med exempel)

v₁ = 0 Yo +tjugo J m

Från ritningen observeras att vektor 2 är:

v₂ = -10 Yo - tjugo J m

Vektor 3 är horisontell och pekar i den positiva adressen:

v₃ = 10 Yo + 0 J  m

Slutligen är vektor 4 lutande 45 º, eftersom det är diagonalen på torget, därför mäter dess komponenter samma:

v₄ = -10 Yo + 10 J m

Observera att skylten -.

Den resulterande vektorn erhålls genom att lägga till komponentkomponent:

v_R = -10 Yo + 10 J m

Då är systemets balansvektor:

v_OCH = 10 Yo - 10 J m

Referenser

1. Beardon, T. 2011. En introduktion till vektorer. Återhämtat sig från: nrich.Matte.org.
2. Bedford, 2000. TILL. Mekanik för teknik: statisk. Addison Wesley. 38-52.
3. Figueroa, D. Serie: Physics for Science and Engineering. Volym 1. Kinematik.31-68.
4. Fysisk. Modul 8: Vektorer. Återhämtat sig från: frtl.Utn.Edu.ar
5. Hibbeler, R. 2006. Mekanik för ingenjörer. Statisk. Sjätte upplagan. Continental Editor Company. 15-53.
6. Tilläggskalkylatorvektor. Återhämtat sig från: 1728.org
7. Vektorer. Återhämtat sig från: Wikibooks.org