Vektorer i rymden hur man grafer, applikationer, övningar

En vektor i rymden Allt representeras av ett koordinatsystem som ges av x, och och z. Nästan alltid planet Xy Det är planet på den horisontella ytan och axeln z representerar höjden (eller djupet).

De kartesiska koordinataxlarna som visas i figur 1, dela utrymmet i 8 regioner som heter Oärter, analogt med hur axlarna x - och Dela upp planet i fyra kvadranter. Vi kommer då att ha 1 oktant, 2: a ocanto och så vidare.

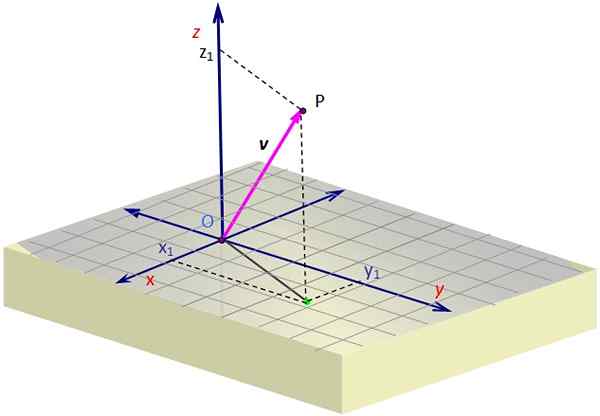
Figur 1. En vektor i rymden. Källa: Självgjord.

Figur 1 innehåller en representation av en vektor v i rymden. Vissa perspektiv krävs för att skapa en illusion av tre dimensioner på skärmens plan, vilket uppnås genom att rita en sned vy.

För att grafera en 3D -vektor måste du hjälpa de streckade linjerna som bestämmer koordinaterna för projektets projektion eller "skugga" v Över ytan x-och. Denna projektion börjar i O och slutar vid den gröna punkten.

När du är där måste du fortsätta med den vertikala till höjden (eller djupet) nödvändigt beroende på värdet av z, tills du kommer till P. Vektorn dras från O och slutar i P, som i exemplet är i den första Ocant.

[TOC]

Ansökningar

Vektorer i rymden används allmänt i mekanik och andra grenar av fysik och teknik, eftersom strukturerna som omger oss kräver geometri i de tre dimensionerna.

Positionvektorer i rymden används för att placera objekt med avseende på en referenspunkt som heter ursprung ANTINGEN. Därför är de också nödvändiga verktyg i navigering, men det är inte allt.

Kan tjäna dig: elektromagnetiska vågor: Maxwell teori, typer, egenskaper

Krafterna som verkar på strukturer som bultar, stöd, kablar, stagar och mer är vektor natur och är orienterade i rymden. För att veta dess effekt är det nödvändigt att veta din adress (och även din ansökningspunkt).

Och ofta är riktningen för en styrka känd av två punkter i rymden som tillhör dess handlingslinje. På detta sätt är kraften:

F = F eller

Där f är storleken eller modulen för kraft och eller Det är enhetsvektorn (modul 1) riktad längs handlingslinjen F. 

3D -vektorotation och representationer

Innan du löser några exempel kommer notationen av 3D -vektorer att granskas kort.

I exemplet i figur 1 har vektor V, vars ursprungspunkt sammanfaller med ursprunget eller vars slut är punkt P, har koordinater x och z Positiv, medan han koordinerar och Det är negativt. Dessa koordinater är: x₁, och₁, z₁, som är just koordinaterna för P.

Så om vi har en vektor kopplad till ursprunget, det vill säga vars utgångspunkt sammanfaller med O, är det mycket lätt att indikera dess koordinater, som kommer att vara de extrema punkten eller P. För att skilja mellan en punkt och en vektor kommer vi att använda för de senaste djärva bokstäverna och parenteserna, så här:

v = < x₁, och₁, z₁ >

Medan punkt P betecknas med parenteser:

P = (x₁, och₁, z₁)

En annan representation använder enhetsvektorer Yo, J och k som definierar de tre rymdriktningarna i axlarna x, och och z respektive.

Dessa vektorer är vinkelräta mot varandra och utgör en Ortonormal bas (Se figur 2). Detta innebär att en 3D -vektor kan skrivas i termer av dem som:

Kan tjäna dig: böljande rörelse: egenskaper, typer av vågor, exempel

v = v_x Yo + v_och J + v_z k

Vinklar och kosenos direktörer för en vektor

Figur 2 visar också styrelseledamöterna γ -vinklar₁, y₂ och y₃ än vektorn v respektive med axlarna x, och och z. Genom att känna till dessa vinklar och storleken på vektorn är detta helt bestämd. Dessutom uppfyller styrelseledamöternas kosinuser följande förhållande:

(cos γ₁)² + (cos γ₂)² + (cos γ₃)² = 1

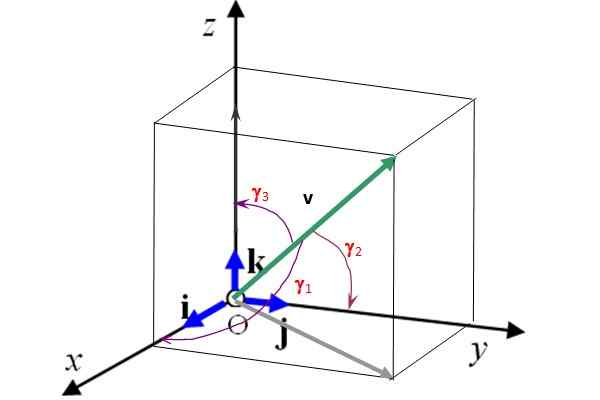figur 2. Enhetsvektorer I, J och K bestämmer de tre förmånsriktningarna för rymden. Källa: Självgjord.

Löst övningar

-Övning 1

I figur 2 y -vinklarna₁, y₂ och y₃ än vektorn v av modul 50 -formulär med koordinataxlarna är respektive: 75.0º, 60.0º och 34.3: e. Hitta de kartesiska komponenterna i denna vektor och representera den i termer av enhetsvektorerna Yo, J och k.

Lösning

Projicering av vektorn v på axeln x är v_x = 50 . Cos 75º = 12.941. På samma sätt projiceringen av v på axeln och är v_och = 50 cos 60 º = 25 och slutligen på axeln z är v_z = 50. cos 34.3: e = 41.3. Nu v kan uttryckas som:

v = 12.9 Yo + 25.0 J + 41.3 k

-Övning 2 

Hitta spänningar i var och en av kablarna som håller hinken i figuren som är i jämvikt, om vikten på detta är 30 n.

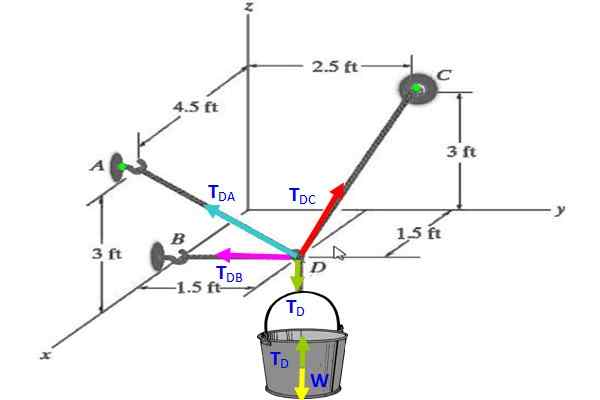Figur 3. Spänningsdiagram för övning 2.

Lösning

På hinken indikerar det fria kroppsdiagret det T_D (grönt) kompenserar för vikt W (gul), därför t_D = W = 30 n.

I knuten, vektorn T_D  Det riktas vertikalt ner, då:

T_D = 30 (-k) N.

För att fastställa de återstående spänningarna måste du följa följande steg:

Steg 1: Hitta koordinaterna för alla punkter

A = (4.5; 0; 3) (A är på väggplanet X-z)

B = (1.5; 0; 0) (B är på X -axeln)

Kan tjäna dig: adress (fysisk)

C = (0, 2.5, 3) (C är på väggplanet och z)

D = (1.5; 1.5; 0) (D är på det horisontella planet  x-och)

Steg 2: Hitta vektorerna i varje riktning genom att subtrahera slutet och början

Ger =

Likström =

DB =

Steg 3: Beräkna moduler och enhetsvektorer

En enhetsvektor erhålls genom uttryck: eller = r / r, med r (i djärv) att vara vektorn och r (utan djärv) modulen för nämnda vektor.

Da = (3² + (-1.5)² + 3²)^½ = 4.5; Dc = ((-1.5) ² + 1² + 3²)^½ = 3.5

eller_Ger = 4.5 =

eller_Likström = 3.5 =

eller_DB =

eller_D =

Steg 4: Uttryck alla spänningar som vektorer

T_Ger = T_Ger eller_Ger = T_Ger

T_Likström = T_Likström eller_{DC =}  T_Likström

T_DB = T_DB eller_DB = T_DB

 T_D = 30

Steg 5: Applicera det statiska jämviktstillståndet och lösa ekvationssystemet

Slutligen appliceras det statiska balansförhållandet på skopan, så att vektor summan av alla krafter på knuten är ogiltig:

T_Ger + T_Likström + T_DB + T_D = 0

Eftersom spänningarna är i rymden kommer det att leda till ett tre ekvationssystem för varje komponent (x, och och z) av spänningar.

0.67 t_Ger -0.43 t_Likström + 0 t_DB = 0

-0.33 t_Ger + 0.29 t_Likström - T_DB = 0

0.67 t_Ger + 0.86 t_Likström +0 t_DB - 30 = 0

Lösningen är: t_Ger = 14.9 n; T_Ger = 23.3 n; T_DB = 1.82 n

Referenser

1. Bedford, 2000. TILL. Mekanik för teknik: statisk. Addison Wesley. 38-52.
2. Figueroa, D. Serie: Physics for Science and Engineering. Volym 1. Kinematik.31-68.
3. Fysisk. Modul 8: Vektorer. Återhämtat sig från: frtl.Utn.Edu.ar
4. Hibbeler, R. 2006. Mekanik för ingenjörer. Statisk. Sjätte upplagan. Continental Editor Company. 15-53.
5. Tilläggskalkylatorvektor. Återhämtat sig från: 1728.org