Atomvolym

Vad är atomvolym?

han Atomvolym Det är ett relativt värde som indikerar förhållandet mellan det molmassan för ett element och dess densitet. Sedan beror denna volym på elementets densitet, och densiteten beror på fasen och hur atomer beställs inom detta.

Så att atomvolymen för ett Z -element inte är densamma i en annan annan fas än att den uppvisar vid rumstemperatur (flytande, fast eller gas), eller när det är en del av vissa föreningar. Således skiljer sig atomvolymen Z i Zb -föreningen från Z i ZB -föreningen.

Därför att? För att förstå det är det nödvändigt att jämföra atomerna med till exempel vissa kulor. Marbles har sin materialgräns mycket väl definierad, vilket observeras tack vare deras lysande yta. Å andra sidan är gränsen till atomer diffus, även om de kan betraktas som avlägsna sfäriska.

Det som bestämmer en punkt utöver atomgränsen är således tomrummet att hitta en elektron, och denna punkt kan vara längre eller närmare kärnan beroende på hur många angränsande atomer som interagerar runt atomen som beaktas.

Atomvolym och radio

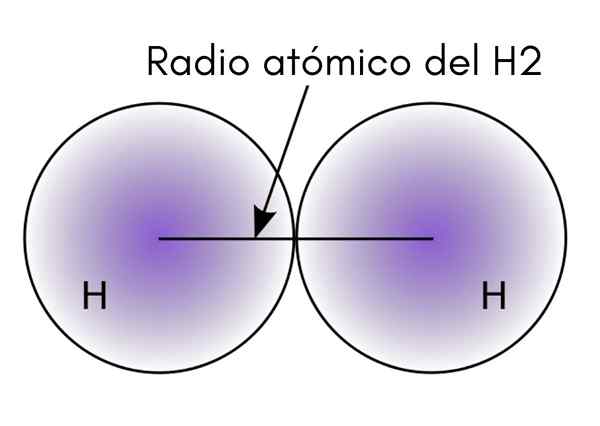
När du interagerar två H -atomer i H -molekylen₂, Positionerna för deras kärnor definieras såväl som avståndet mellan dem (internukleära avstånd). Om båda atomerna är sfäriska är radien avståndet mellan kärnan och den diffusa gränsen:

I den överlägsna bilden kan man se hur sannolikheten för att hitta en elektron minskar när den rör sig bort från kärnan. Dela med två det internukleära avståndet erhålls atomradie. Sedan, förutsatt en sfärisk geometri för atomer, används formeln för att beräkna volymen på en sfär:

V = (4/3) (pi) r³

I detta uttryck är R atomradie som bestäms för H -molekylen₂. V -värdet beräknat med denna lilla exakta metod kan ändras om till exempel H övervägs₂ i flytande eller metalliskt tillstånd. Men denna metod är mycket felaktig eftersom formerna av atomer är mycket långt ifrån den ideala sfären i deras interaktioner.

För att bestämma atomvolymer i fasta ämnen beaktas många variabler som rör arrangemanget, och som erhålls av x -ray -diffraktionsstudier.

Ytterligare formel

Den molära massan uttrycker mängden materia som har en mol atomer i ett kemiskt element.

Dess enheter är g/mol. Å andra sidan är densiteten volymen som upptar ett gram av elementet: g/ml. Eftersom atomvolymenheterna är ML/mol måste du spela med variablerna för att nå de önskade enheterna:

• (g/mol) (ml/g) = ml/mol

Eller vad är detsamma:

• (Molmassa) (1/d) = v
• (Molmassa/d) = v

Således kan volymen av en mol av atomer i ett element enkelt beräkna; Medan med formeln för den sfäriska volymen beräknas volymen för en individuell atom.

För att nå detta värde från den första är en konvertering nödvändig genom Avogadro -numret (6.02 · 10^-23).

Hur varierar atomvolymen i den periodiska tabellen?

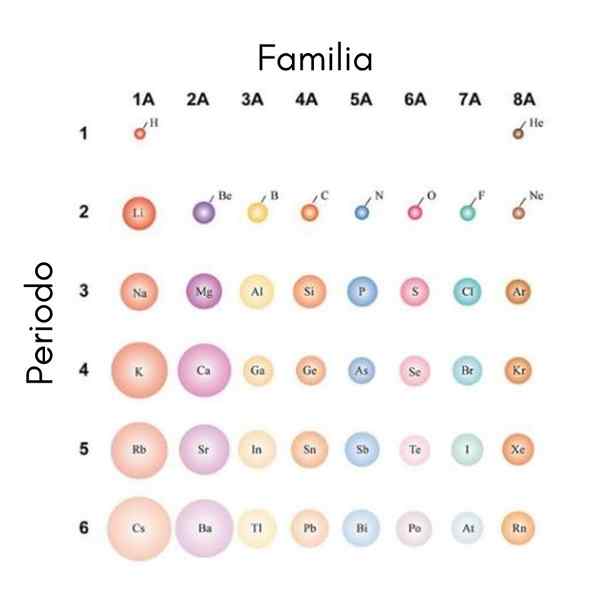
Om atomerna betraktas som sfäriska, kommer deras variation att vara densamma som observeras i atomradio. I den överlägsna bilden, som visar de representativa elementen, illustreras det att från höger till vänster atomer dvärg; Å andra sidan, från topp till botten blir dessa mer skrymmande.

Detta beror på att kärnan under samma period innehåller protoner när den rör sig till höger. Dessa protoner utövar en attraktionskraft på externa elektroner, som känner en effektiv kärnbelastning z_Ef, mindre än verklig kärnbelastning z.

Elektronerna i de inre skikten avvisar de i det yttre skiktet, vilket minskar effekten av kärnan på dem; Detta kallas skärmeffekten. Under samma period misslyckas skärmeffekten med att motverka ökningen av antalet protoner, så att elektronerna i det inre skiktet inte förhindrar sammandragning av atomer.

Men när de faller ner i en grupp är nya energinivåer aktiverade, vilket gör det möjligt för elektroner att kretsa i kärnan. På samma sätt ökas antalet elektroner i det inre skiktet, vars skärmningseffekter börjar minskas om kärnan lägger till protoner igen.

Av dessa skäl uppskattas att grupp 1A har de mest skrymmande atomerna, till skillnad från de små atomerna i grupp 8a (eller 18), den av ädla gaser.

Atomvolymer av övergångsmetaller

Atomerna i övergångsmetaller integrerar elektroner i inre orbitaler d. Denna ökning av skärmeffekten och såväl som den verkliga kärnbelastningen Z är nästan lika upphävda, så deras atomer behåller liknande storlek under samma period.

Med andra ord: Under en period uppvisar övergångsmetaller liknande atomvolymer. Dessa små skillnader är emellertid oerhört betydelsefulla när man definierar metallkristaller (som om de var metalliska kulor).

Atomvolymexempel

Två matematiska formler finns tillgängliga för att beräkna atomvolymen för ett element, var och en med motsvarande exempel.

Exempel 1

Med tanke på atomradiogrogen -37 pm (1 picometer = 10^-12m) -och cesium -265 pm-, beräkna dina atomvolymer.

Med hjälp av den sfäriska volymformeln har du då:

V_H= (4/3) (3.14) (37 pm)³= 212.07³

V_Cs= (4/3) (3.14) (265 pm)³= 77912297.67³

Dessa volymer uttryckta i picometrar är emellertid exorbitanta, så de förvandlas till AngStroms -enheter, vilket multiplicerar dem med omvandlingsfaktorn (1å/100pm)³:

(212.07³) (1å/100pm)³= 2,1207 × 10^-4 TILL³

(77912297.67³) (1å/100pm)³= 77 912 ų

Således bevisas skillnaderna i storlek mellan den lilla H -atomen och den voluminösa atomen i CS numeriskt. Det är nödvändigt att ta hänsyn till att dessa beräkningar inte är mer än approximationer enligt uttalandet att en atom är helt sfärisk, vilket avvisar verkligheten.

Exempel 2

Densiteten för rent guld är 19,32 g/ml och dess molmassa är 196,97 g/mol. Tillämpa M/D -formeln för att beräkna volymen på en mol guldatomer är följande:

V_Au= (196,97 g/mol)/(19,32 g/ml) = 10,19 ml/mol

Det vill säga att 1 mol guldatomer upptar 10,19 ml, men vilken volym upptar en guldatom specifikt? Och hur man uttrycker det i PM -enheter³? För detta, tillämpa bara följande konverteringsfaktorer:

(10.19 ml/mol) · (mol/6.02 · 10^-23 atomer) · (1 m/100 cm)³· (13:00/10^-12m)³= 16,92 · 10⁶ p.m³

Å andra sidan är Atomic Radie of Gold 166 PM. Om båda volymerna jämförs - den som erhålls med föregående metod och som beräknas med formeln för den sfäriska volymen - kommer det att konstateras att de inte har samma värde:

V_Au= (4/3) (3.14) (166)³= 19,15 · 10⁶ p.m³

Vilken av de två är närmare det accepterade värdet? Den som är närmast de experimentella resultaten som erhålls genom röntgendiffraktion av den kristallina strukturen hos guld.