Molvolymkoncept och formel, beräkning och exempel

han molvolym Det är en intensiv egenskap som indikerar hur mycket utrymme en mol av en bestämning eller förening upptar. Representeras av symbol V_m, och uttrycks i DM -enheter³/mol för gaser och cm³/mol för vätskor och fasta ämnen, eftersom de senare är mer begränsade av deras största intermolekylära krafter.

Den här egenskapen återkommer när man studerar termodynamiska system som involverar gaser; Sedan, för vätskor och fasta ämnen för att bestämma v_m De blir mer komplicerade och felaktiga. Därför, när det gäller grundläggande kurser, är molvolym alltid associerad med idealisk gasteori.

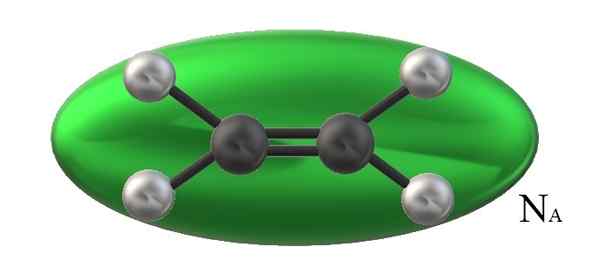
Volymen av en etenmolekyl är ytligt begränsad av den gröna ellipsoiden och antalet avogadro gånger detta belopp. Källa: Gabriel Bolívar.

Detta beror på att de perfekta eller perfekta gaserna är strukturella aspekter irrelevanta; Alla dess partiklar visualiseras som sfärer som kolliderar elastiskt med varandra och uppför sig på samma sätt oavsett vad deras massor eller egenskaper är.

Således kommer en mol av alla idealiska gaser att uppta, vid viss tryck och temperatur, samma volym v_m. Det sägs att under normala förhållanden för P och T, 1 atm respektive 0 ºC kommer en mol av en idealisk gas att uppta en volym på 22,4 liter. Detta värde är användbart och ungefärligt även när verkliga gaser utvärderas.

[TOC]

Koncept och formel

För gaser

Den omedelbara formeln för att beräkna den molära volymen för en art är:

V_m = V/n

Där v är volymen den upptar, och n Mängden av arter i mol. Problemet är att v_m Det beror på trycket och temperaturen som upplever av molekyler, och ett matematiskt uttryck önskas att ta hänsyn till dessa variabler.

Kan tjäna dig: Moleality

Bildens eten, h₂C = ch₂, Den har en molekylär volym associerad och begränsad av en grön ellipsoid. Detta h₂C = ch₂ Det kan rotera på flera sätt, vilket är som om det rörde sig i rymden sa ellipsoid för att visualisera hur mycket volym det skulle uppta (uppenbarligen föraktligt).

Men om volymen av en sådan grön ellipsoid multiplicerar vi den med n_TILL, Avogadro -numret kommer då att ha en mol etylenmolekyler; en mol av ellipsoid som interagerar med varandra. Vid en högre temperatur kommer molekylerna att skilja sig från varandra; Medan de är större tryck kommer de att dra sig och minska sin volym.

Därför v_m är beroende av p och t. Etylen är platt geometri, så det kan inte tänka att dess v_m Vara korrekt och exakt samma som metan, cho₄, av tetraedral geometri och kan representeras med en sfär och inte en ellipsoid.

För vätskor och fasta ämnen

Molekylerna eller atomerna av vätskor och fasta ämnen har också sin egen V_m, som kan relateras till din densitet:

V_m = m/(d · n)

Temperaturen påverkar molvolymen mer för vätskor och fasta ämnen än trycket, så länge det senare inte varierar kraftigt eller exorbitant (i ordningen av GPA). På samma sätt, som nämnts med eten, har geometrier och molekylstrukturer ett stort inflytande på värdena på V_m.

Under normala förhållanden observeras emellertid att tätheter för olika vätskor eller fasta ämnen inte varierar för mycket i sina storlekar; Detsamma gäller för dess molvolymer. Observera att de tätaste de är, den lägre V_m.

Beträffande fasta ämnen beror dess molvolym också på dess kristallina strukturer (volymen på dess enhetscell).

Kan tjäna dig: kaliumbifttalat: struktur, nomenklatur, användningar, risker

Hur man beräknar molvolym?

Till skillnad från vätskor och fasta ämnen finns det för idealiska gaser en ekvation som gör att du kan beräkna v_m beroende på P och T och dess förändringar; Detta är det för idealiska gaser:

P = nrt/v

Vilket är tillmötesgående att uttrycka V/N:

V/n = rt/p

V_m = Rt/p

Om vi ​​använder gaskonstanten r = 0,082 l · atm · k^-1· Mol^-1, Då måste temperaturen uttryckas i Kelvin (K) och trycket i atmosfärer. Observera att det observeras här varför v_m Det är en intensiv egenskap: T och P har inget att göra med gasens massa utan med sin volym.

Dessa beräkningar är endast giltiga under förhållanden där gaser uppför sig nära idealitet. Värdena som erhållits genom experiment har emellertid en liten marginal i förhållande till teoretiker.

Exempel på molvolymberäkning

Exempel 1

Du har en gas och vars densitet är 8,5 · 10^-4 g/cm³. Om du har 16 gram motsvarande 0,92 mol y, beräkna din molvolym.

Från densitetsformeln kan vi beräkna vilken volym av och uppta sådana 16 gram:

V = 16 g/ (8,5 · 10^-4 g/cm³)

= 18.823,52 cm³ eller 18,82 l

Så v_m Det beräknas direkt genom att dela denna volym mellan mängden given mol:

V_m = 18,82 l/0,92 mol

= 20,45 l/mol o l · mol^-1 eller DM³· Mol^-1

Övning 2

I föregående exempel på och inte specificerades vid någon tidpunkt vad som var temperaturen som upplevdes av nämnda gaspartiklar. Antagande att det fungerade med och vid atmosfärstryck, beräkna den temperatur som krävs för att komprimera den till den bestämda molvolymen.

Kan tjäna dig: förpackningsfaktor

Träningsuttalandet är längre än dess resolution. Vi vänder oss till ekvationen:

V_m = Rt/p

Men vi rensar och vet att atmosfärstrycket är 1 atm, vi löser:

T = v_mP/r

= (20,45 l/mol) (1 atm)/(0,082 l · atm/k · mol)

= 249.39 K

Det vill säga en mol och kommer att uppta 20,45 liter vid en temperatur nära -23,76 ºC.

Övning 3

Efter ovanstående resultat, bestäm v_m vid 0 ºC, 25 ° C och vid absolut noll vid atmosfärstryck.

Omvandla temperaturen till Kelvin har vi första 273,17 K, 298,15 K och 0 K. Vi löser direkt genom att ersätta för första och andra temperaturer:

V_m = Rt/p

= (0,082 l · atm/ k · mol) (273,15 k)/ 1 atm

= 22,40 L/mol (0 ºC)

= (0,082 l · atm/ k · mol) (298,15 k)/ 1 atm

= 24,45 L/mol (25 ° C)

Värdet av 22,4 liter nämndes i början. Observera hur v_m öka med temperaturen. När du vill göra samma beräkning med absolut noll snubblar vi över den tredje lagen om termodynamik:

(0,082 l · atm/ k · mol) (0 k)/ 1 atm

= 0 L/mol (-273,15 ºC)

Gasen och kan inte ha en icke -existerande molvolym; Det betyder att det har blivit en vätska och föregående ekvation är inte längre giltig.

Å andra sidan, omöjligt att beräkna v_m I Absolute Zero följer den tredje lagen om termodynamik, som säger att det är omöjligt att kyla något ämne vid temperaturen på absolut noll.

Referenser

1. Iran. Levin. (2014). Principer för fysikalik. Sjätte upplagan. MC Graw Hill.
2. Glanssten. (1970). Fysisk kemifördrag. Andra upplagan. Aguilar.
3. Wikipedia. (2019). Molvolym. Hämtad från: i.Wikipedia.org
4. Helmestine, Anne Marie, PH.D. (8 augusti 2019). Molvolymdefinition i kemi. Återhämtat sig från: tankco.com
5. Byju. (2019). Molvolymformel. Återhämtat sig från: byju.com
6. González Mónica. (28 oktober 2010). Molvolym. Återhämtat sig från: kemi.Laguia2000.com