Boltzmann Konstant historia, ekvationer, beräkning, övningar

De Boltzmann konstant Det är värdet som relaterar den genomsnittliga kinetiska energin i ett termodynamiskt system eller ett objekt med den absoluta temperaturen på samma. Även om de ofta är förvirrade är temperatur och energi inte samma koncept.

Temperaturen är ett mått på energi, men inte själva energin. Med Boltzmann -konstanten är en kopplad till varandra enligt följande:

OCH_c = (3/2) k_B  T

Boltzmann -värd i Wien. Källa: Dadotet på English Wikipedia [CC BY-SA 3.0 (http: // Creativecommons.Org/licenser/BY-SA/3.0/]]

Denna ekvation är giltig för en idealisk monoatomisk gasmolekyl m, var OCH_c Det är hans kinetiska energi som ges i Joules, K_B Det är Boltzmanns konstant och T Det är den absoluta temperaturen i Kelvin.

På detta sätt, när temperaturen ökar, ökar den genomsnittliga kinetiska energin med substansmolekyl också, som förväntat ska hända. Och det motsatta händer när temperaturen minskar och kan nå den punkt där hela rörelsen upphör, den lägsta möjliga eller absoluta temperaturen uppnås.

När man pratar om genomsnittlig kinetisk energi är det nödvändigt att komma ihåg att kinetisk energi är associerad med rörelse. Och partiklarna kan röra sig på många sätt, till exempel att flytta, rotera eller vibrera. Naturligtvis kommer inte alla att göra det på samma sätt, och eftersom de är otaliga, tas genomsnittet för att karakterisera systemet.

Vissa energistillstånd är mer benägna än andra. Detta koncept är av radikal betydelse vid termodynamik. Energin som beaktas i föregående ekvation är kinetisk energi från översättning. Av sannolikheten för staterna och deras förhållande till Boltzmann -konstanten kommer att prata lite senare.

2018 omdefinierades Kelvin och med honom Boltzmann -konstanten, som i det internationella systemet är ungefär 1.380649 x 10^-23 J. K^-1. Mycket mer precision kan uppnås för Boltzmann -konstanten, som har bestämts i många laboratorier runt om i världen, med olika metoder.

[TOC]

Historia

Den berömda konstanten är skyldig sitt namn till fysikern Ludwig Boltzmann (1844-1906), född i Wien, som ägnade sitt liv som forskare till studien av det statistiska beteendet hos systemen med många partiklar, ur Newtonian-mekanikens synvinkel.

Även om atomens existens är allmänt accepterad, under 1800 -talet var tron ​​på huruvida atomen verkligen fanns eller var en artifice som många fysiska fenomen förklarades i full debatt.

Kan tjäna dig: Normal vektor: beräkning och exempel

Boltzmann var en stark försvarare av Atoms existens, och under sin tid mötte han hård kritik av sitt arbete av många kollegor, som ansåg att de innehöll olösliga paradoxer.

Han förklarade att observerbara fenomen på makroskopiska nivåer kunde förklaras genom de statistiska egenskaperna hos beståndsdelar som atomer och molekyler.

Denna kritik kan bero på det djupa avsnittet av depression som ledde till att han tog sitt eget liv i början av september 1906, då han fortfarande hade mycket att göra, eftersom han ansågs vara en av de stora teoretiska fysikerna i sin tid och där var lite till att andra forskare kommer att bidra till att bekräfta sanningen i sina teorier.

Det hände inte länge efter hans död när nya upptäckter om atomens natur och hans konstituerande partiklar skulle läggas till för att ge orsaken till Boltzmann.

Boltzmanns ständiga och Plancks verk

Nu, Boltzmanns konstant k_B Det introducerades som det är känt idag ett tag efter den österrikiska fysikerns arbete. Det var Max Planck, i hans lag om utsläppet av den svarta kroppen, ett verk som han presenterade 1901, som vid den tiden gav honom värdet av 1,34 x 10²³ J/k.

År 1933 lades Boltzmann till Wien som en affischhyllning en plack med definitionen av entropi som involverar den berömda konstanten: S = k_B log w, ekvation som kommer att diskuteras senare.

Idag är Boltzmanns konstant nödvändig i tillämpningen av de termodynamiska lagarna, statistisk mekanik och informationsteori, som denna fysiker med sorgligt slut var en pionjär.

Värde och ekvationer

Gaser kan beskrivas i makroskopiska termer och även i mikroskopiska termer. För den första beskrivningen finns koncept som densitet, temperatur och tryck.

Det bör emellertid komma ihåg att en gas består av många partiklar, som har en global tendens till ett visst beteende. Det är den trenden som mäts makroskopiskt. Ett sätt att bestämma Boltzmanns konstant är tack vare den välkända ekvationen av idealiska gaser:

p.V = n. R. T

Här p Det är gastrycket, V Det är dess volym, n Det är antalet närvarande mullvader, R Det är gasens konstant T Det är temperaturen. I en mol av idealisk gas uppfylls följande förhållande mellan produkten p.V, och den kinetiska energin i översättningen K Hela uppsättningen är:

Kan tjäna dig: Korpuskulär Model of Matter

p.V = (2/3). K

Därför är kinetisk energi:

K = (3/2) n.R.T

Genom att dela med det totala antalet närvarande molekyler, som kommer att kallas N, erhålls den genomsnittliga kinetiska energin för en enda partikel:

OCH_c = K /n

OCH_c= (3/2n) n.R.T

I en mol finns antalet partiklar n_TILL, Och därför är det totala antalet partiklar N = nnA, Visting:

OCH_c = (3/2nn_TILL) n.R.T

Precis kvoten R/n_TILL Det är Boltzmanns konstant och demonstreras att den kinetiska energin för genomsnittlig översättning av en partikel endast beror på den absoluta temperaturen och inte andra storlekar såsom tryck, volym eller till och med typen av molekyl:

OCH_c = (3/2) k_B. T

Boltzmanns konstant och entropi

En gas har en given temperatur, men den temperaturen kan motsvara olika inre energitillstånd. Hur man visualiserar denna skillnad?

Tänk på den samtidiga lanseringen av fyra mynt och hur de kan falla:

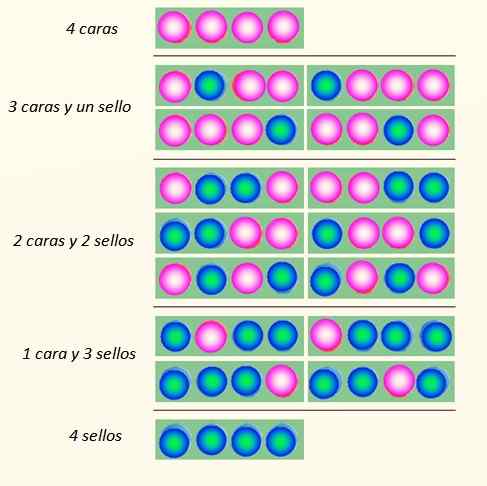Sätt på vilka fyra mynt kan falla. Källa: Självgjord

Myntuppsättningen kan anta totalt 5 stater, som övervägs Makroskopisk, beskrivs i figuren. Vilka av dessa stater skulle läsaren säga att det är det mest troliga?

Svaret bör vara tillståndet för 2 ansikten och 2 kors, eftersom det har totalt 6 möjligheter, av de 16 illustrerade i figuren. Och 2⁴ = 16. Dessa motsvarar staterna mikroskopisk.

Och vad händer om 20 mynt lanseras istället för 4? Det skulle finnas totalt 2^tjugo Möjligheter eller "mikroskopiska tillstånd". Det är ett mycket större och svårare antal att hantera. För att underlätta hanteringen av stora antal är logaritmer mycket lämpliga.

Det som verkar uppenbart är att staten med den största störningen är det mest troliga. De mest beställda staterna som 4 ansikten eller 4 stämplar är lite mindre troliga.

Entropin av ett makroskopiskt tillstånd definieras som:

S = k_B ln w

Var W Det är antalet möjliga mikroskopiska tillstånd och k_B Det är Boltzmanns konstant. Som ln w Det är måttlöst, entropi har samma enheter som k_B: Joule/k.

Detta är den berömda ekvationen i Boltzmanns gravsten i Wien. Men mer än entropi är relevant förändringen av det:

Det kan tjäna dig: termodynamiska variabler: vilka är och övningar löst

ΔS = k_B ln w₂ - k_B ln w₁ = k_B ln (w₂/w₁)

Hur beräknas K_B?

Värdet på Boltzmann -konstanten erhålls experimentellt exakt med mätningar baserade på akustisk termometri, som utförs med hjälp av egenskapen som fastställer beroendet av ljudets hastighet i en gas med temperaturen på samma.

I själva verket ges ljudets hastighet i en gas av:

Där b _adiabatisk Det är den adiabatiska kompressibilitetsmodulen som ges av:

B_adiabatisk = yp

Och ρ är gastäthet. För föregående ekvation, p Det är trycket på gasen i fråga och y Det är den adiabatiska koefficienten, vars värde för en specifik gas finns i tabellerna.

Metrologiska institut upplever också andra sätt att mäta konstanten, till exempel Johnson Noise Thermometry, som använder de termiska fluktuationerna som förekommer slumpmässigt i materialen, särskilt i förare.

Löst övningar

-Övning 1

Hitta:

a) Den kinetiska energin från genomsnittlig översättning OCH_c som har en idealisk gasmolekyl vid 25 ºC

b) den kinetiska energin i översättningen K av molekylerna i 1 mol av denna gas

c) Medelhastigheten för en syremolekyl vid 25 ºC

Faktum

m_syre = 16 x 10 ^-3 kg/mol

Lösning

till) OCH_c = (3/2) k t = 1.5 x 1.380649 x 10^-23J. K^-1 x 298 K = 6.2 x 10^-tjugoett J

b) K = (3/2) n.R.T = 5 x 1 mol x 8.314 j/mol .K x 298 K = 3716 J

c) OCH_c = ½ mV², Med hänsyn till att syremolekylen är diatomisk och molmassan måste multipliceras med 2, kommer det att vara:

-Övning 2

Hitta byte av entropi när 1 mol gas ockuperat med en volym på 0.5 m³ Det expanderar till att ockupera 1 m³.

Lösning

ΔS = k_B ln (w₂/w₁)

W₂= 2^NW₁ (Det fanns 2⁴ Mikroskopiska tillstånd för lanseringen av de fyra mynten, kom ihåg?)

Där n är antalet partiklar närvarande i 0.5 mol gas 0.5 x n_TILL:

ΔS = k_B ln (2^N W₁/w₁) = k_B ln 2^N= k_B 0.5n_TILL ln 2 = 2.88 j/k

Referenser

1. Atkins, s. 1999. Fysisk kemi. Omega -utgåvor. 13-47.
2. Bauer, w. 2011. Fysik för teknik och vetenskap. Volym 1. MC Graw Hill. 664-672.
3. Giancoli, D.  2006. Fysik: Principer med applikationer. 6: e ... Ed Prentice Hall. 443 -444.
4. Sears, Zemansky. 2016. Universitetsfysik med modern fysik. 14th. Ed. Volym 1. 647-673.
5. Om omdefinition. Kelvin: Boltzmann Constant. Återhämtat sig från: nist.Gov